35 Частотные характеристики

Частотная передаточная функция может быть представлена в следующих видах:

W(j) = A() e ^j),      или    W(j) = U() + jV() ;

где:

• A() - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя:

A() = (k₁² + k₂² ²)^1/2 / ((1 - T₂² ²)² + T₁² ²)^1/2 .

•  - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя:

= arctg(k₂ / k₁) - arctg(T₁ / (1-T₂²)).

• U() и V() - вещественная и мнимая части частотной ПФ. Для их нахождения немобходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.

Амплитудно-фазовая (частотная) характеристика или годограф Найквиста

Амплитудно-фазовая характеристика (годограф Найквиста)- Графическое отображение для всех частот спектра отношений выходного сигнала САУ к входному, представленных в комплексной форме. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка.

От АФХ порождаются все другие частотные зависимости:

• U() - четная (для замкнутых САУ P());

• V() - нечетная;

• A() - четная (АЧХ);

•  - нечетная (ФЧХ);

• ЛАЧХ & ЛФЧХ - используются наиболее часто.

Логарифмические чх - лачх & лфчх

Построение ЛАЧХ & ЛФЧХ производится по выражениям:

L() = 20 lg |W(j)| = 20 lg A(),  [дБ];    = arg(W(j)),  [рад].

Числитель и знаменатель ПФ САР могут быть представлены либо в виде отношения полиномов:

,

либо в виде отношения их разложений на элементарные множители:

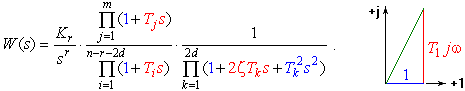(1)

Подстановка sj позволяет перейти в частотный домен. При наличии ЭВМ построение ЛАЧХ & ЛФЧХ не составит труда  в любом случае. Однако разложенная на множители ПФ (1) позволяет построить асимптотические ЛАЧХ & ЛФЧХ практически без вычислительной работы. Каждый линейный множитель ее числителя и знаменателя есть комплексное число. Найдем модуль каждого (как гипотенузу прямоугольного треугольника), и перейдем к логарифмическому масштабу:

.

Для упрощения дальнейших построений избавимся от операции умножения, заменив ее операцией сложения в логарифмическом домене:

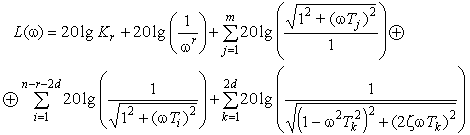(2).

Легко понять, что каждое слагаемое выражения (2) есть либо прямая линия, либо асимптотически приближается к прямым линиям при устремлении частоты к нулю и к бесконечности. Наклон аппроксимирующих прямых всегда кратен 20 дБ за декаду.

Для построения ЛФЧХ необходимо найти фазу каждого множителя числителя и знаменателя частотной ПФ, как арктангенс отношения его противолежащего катета к прилежащему (напомним, что при произведении комплексных чисел (в экспоненциальной форме) фазы (показатели степени) складываются, а при делении - вычитаются). Таким образом, построение ЛФЧХ производится по выражению:

.

Отметим так же, что одному Белу соответствует увеличение мощности в 10 раз. Поскольку A - это физическая величина либо первого, либо второго рода, а не их произведение (т.е. не мощность); увеличение ее в 10 раз соответствует увеличению мощности в 100 раз, что соответствует двум Белам или 20 дБ.