
kurs_lekcii_mo_matematicheskomu_analizu / Нелинейные операции над векторами
.pdf
ТЕМА 7. НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
1.Скалярное произведение векторов
Определение 1. Скалярным произведением двух векторов a и b называется число, обозначаемое (a, b) и равное произведению длин векторов на косинус угла между ними:
( |
|
|
|
|
|
|
|
|
(1) |
a, b) = |a| · |b| · cos ϕ. |
|||||||||
Скалярное произведение векторов a и b еще обозначают как a · b.
Рис. 1.
Так как по определению проекции |b| · cos ϕ = прab и |a| cos ϕ = прba (рис. 1), то равенство (1) можно представить в двух видах:
(a, b) = |a| · прab = |b| · прba.
Скалярным квадратом вектора a называется скалярное произведение вектора a на себя:
(a, a) = |a| · |a| cos 0o = |a|2,
т. е. скалярный квадрат вектора равен квадрату его длины. Векторы a и b перпендикулярны тогда и только тогда, когда
( |
|
|
|
|
(2) |
a, b) = 0. |
|||||
Скалярное произведение обладает свойствами:
1)переместительности (коммутативности) (a, b) = (b, a);
2)сочетательности (ассоциативности) относительно числового множителя (αa, b) =
α(a, b);
3)распределительности (дистрибутивности) относительно суммы векторов (a, (b + c)) = (a, b) + (a, c).
1

Рассмотрим доказательство третьего свойства, а доказательства первых двух рекомендуем проделать самостоятельно.
(a, (b + c)) = |a| · прa(b + c) = (по св-ву 1 проекций) =
= |a| · (прab + прac) = |a| · прab + |a| · прac = (a, b) + (a, c).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1. Рассмотрим орты i, j, k. Так как |
|
i j |
|
k |
|
|
|
|
|
и i |
|
j, i |
|
k, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
| | = |
|2 |
| = | |
|
| |
= 1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
j k, имеем: |
(i, i) = |i| |
= 1, |
(j, j) = |j| |
= 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
(k, k) = |k| |
= 1, |
|
(i, j) = (i, k) = (j, k) = |
|||||||||||||||||||||||||||||||||||||||||||
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из определения скалярного произведения следует неравенство Коши – Буняковского
|(a, b)| ≤ |a| · |b|.
Получим выражение скалярного произведения через координаты векторов. Пусть a = (X1, Y1, Z1) = X1i + Y1j + Z1k,
b = (X2, Y2, Z2) = X2i + Y2j + Z2k.
(a, b) = ((X1i + Y1j + Z1k), (X2i + Y2j + Z2k)) = (по св-ву 3) =
= (X1i, X2i) + (X1i, Y2j) + (X1i, Z2k) + (Y1j, X2i) + (Y1j, Y2j)+
+(Y1j, Z2k) + (Z1k, X2i) + (Z1k, Y2j) + (Z1k, Z2k) = (по св-ву 2) =
= X1 · X2(i, i) + X1 · Y2(i, j) + X1 · Z2(i, k) + Y1 · X2(j, i)+
+Y1 · Y2(j, j) + Y1 · Z2(j, k) + Z1 · X2(k, i) + Z1 · Y2(k, j) + Z1 · Z2(k, k) = = (по св-ву 1 и замечанию 1) = X1 · X2 + Y1 · Y2 + Z1 · Z2.
Скалярное произведение векторов равно сумме произведений одноименных
координат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
a, b) = X1 · X2 + Y1 · Y2 + Z1 · Z2. |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Если |
|
|
|
|
b, то формула (3) примет вид ( |
|
|
|
|
|
|
) = X12 + Y12 + Z12, но ( |
|
|
|
) = |
|
2, значит, |
|||||||||||||||||||||||
|
a |
|
a |
|
a, |
a |
a, |
a |
a |
||||||||||||||||||||||||||||||||||||
|
|
= X1 |
+ Y1 |
+ Z1 , откуда |
|
a = pX1 + Y1 + Z1 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
|
|
= |
2 |
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
| | |
||||||||||||||||
| | |
|
|
|
| | |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Из формулы (1) можно выразить cos ϕ = |
|
a, b) |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| · |b| |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
Если известны координаты векторов |
|
и b, то, используя формулу (3), получаем |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos ϕ = |
|
|
|
|
|
X1 · X2 + Y1 |
|
· Y2 + Z1 · Z2 |
= q. |
(4) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
pX12 + Y12 + Z12 |
· |
pX22 + Y22 + Z22 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Применяя функцию arccos q, можно определить значение ϕ. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
Если векторы |
|
и b заданы своими координатами, то необходимое и достаточное |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|||||||||||||||||||||||||||||||||||||||||
условие перпендикулярности двух векторов (2) выражается равенством |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 · X2 + Y1 · Y2 + Z1 · Z2 = 0. |
|
|
|
(5) |
|||||||||||||||||||||||||
Пример 1.
2

Даны два вектора: a = (1, −2, 2), b = (2, −2, −1). Найти их скалярное произведение и угол между ними. Чему равно выражение 2(a, a) − 4(a, b) + 5(b, b)?
Решение. Подставляя в формулу (3) координаты векторов a и b, находим
(a, b) = 1 · 2 + (−2) · (−2) + 2 · (−1) = 4.
Так как p
|a| = 12 + (−2)2 + 22 = 3
и |
|
|
|b| = p22 + (−2)2 + (−1)2 = 3, |
||
то по формуле (4) получим |
3 · 3 = |
|
cos( c ) = |
9 |
|
a, b |
4 |
4 . |
Поскольку (a, a) = |a|2 = 9 и (b, b) = |b|2 = 9 , то
2(a, a) − 4(a, b) + 5(b, b) = 2 · 9 − 4 · 4 + 5 · 9 = 47.
Пример 2.
Вычислить, какую работу производит сила F = (2, −1, −4), когда точка ее приложения, двигаясь прямолинейно, перемещается из положения (1, −2, 3) в положение
N (5, −6, 1) .
Решение. В соответствии с определением работы и скалярного произведения получаем
A = (F , s),
где A работа; F вектор действующей силы; s вектор пути.
Найдем вектор s = M N : s = (5 − 1, −6 − (−2), 1 − 3) = (4, −4, −2) . С помощью формулы (3) находим
A = (F , s) = 2 · 4 + (−1) · (−4) + (−2) · (−4) = 20 (ед. работы).
Пример 3.
Дан треугольник с вершинами A(−3, 5, 6) , B(1, −5, 7) , C(8, −3, −1). Найти внутренний угол при вершине A и внешний угол при вершине C .
Решение. Внутренний угол треугольника при вершине A равен углу между векторами AB и AC , а внешний угол при вершине C равен углу между векторами
CB и AC (рекомендуется сделать чертеж).
Находим координаты указанных векторов: AB = (4, −10, 1) , AC = (11, −8, −7),
CB = (−7, −2, 8).
С помощью формулы (4) находим косинусы углов: |
|
|
|
|
|
|
|
||||||||||
\ |
117 |
|
|
|
|
1 |
|
|
|
||||||||
cos(ϕ1) = cos(AB, AC) = |
√ |
|
|
√ |
|
|
|
= |
√ |
|
|
, |
|
||||
117 |
234 |
2 |
|||||||||||||||
\ |
117 |
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
−√2 |
|
||||||||
|
√117√234 |
|
|||||||||||||||
cos(ϕ2) = cos(CB, AC) = |
|
|
− |
|
|
= |
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, ϕ1 = 45o, ϕ2 = 135o .
3

Пример 4. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
При |
каком значении λ векторы |
|
|
= (4, λ, 5) и b = (λ, 2, −6) взаимно |
|||||
a |
|||||||||
перпендикулярны? |
|
|
|
|
|
|
|
||
Решение. Условие перпендикулярности |
( |
|
|
|
|||||
|
|
|
|
|
|
||||
a, b) = 0 в данном случае запишется так: |
|||||||||
4 · λ + 2 |
· λ + 5 · (−6) = 0 или 6 · λ − 30 = 0 , откуда λ = 5. |
||||||||
Пример 5.
Найти вектор x, коллинеарный вектору a = (1, 2, −3) и удовлетворяющий условию
(x, a) = 28 .
Решение. Принимая во внимание условие коллинеарности двух векторов, заключаем, что
x = λ(1, 2, −3) = (λ, 2λ, −3λ),
где λ пока неизвестный коэффициент. Так как (x, a) = 28 , то в соответствии с формулой (3) находим
1 · λ + 2 · 2λ + (−3) · (−3λ) = 28,
или 14λ = 28, откуда λ = 2. Следовательно, x = (12, 4, −6) .
Пример 6.
Найти проекцию вектора a = (4, 3, −7) на ось вектора b = (1, −2, −2).
Решение. По определению скалярного произведения и определению проекции (a, b) = |b| · прba. Выразим из этой формулы прba :
|
|
|
|
|
|
|
|
|
|
= |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
пр |
|
|
a, b) |
, |
||||||||
|
|
|
|
|
|
a |
||||||||||||
|
|
|
|
|
b |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|b| |
|||||
откуда пр |
|
|
|
= |
4 · 1 + 3 · (−2) + (−7) · (−2) |
= |
|
12 |
= 4. |
|||||||||
|
|
a |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
b |
p12 + (−2)2 + (−22) |
3 |
|
|
|
|
|
||||||||||
2.Векторное произведение векторов
Определение 2. Три некомпланарных вектора OA = a, OB = b, OC = c, взятые в указанном порядке ( a первый вектор, b второй, c третий) и имеющие общее начало, называются тройкой векторов a, b, c. Будем смотреть с конца вектора c на плоскость, определяемую векторами a и b . Если кратчайший поворот от вектора a к вектору b совершается против часовой стрелки, то тройка векторов a, b, c называется правой (рис. 2, а); если указанный поворот совершается по часовой стрелке, тройка a, b, c называется левой (рис. 2, б).
4

Рис. 2
Две тройки, обе правые или обе левые, называются тройками одной ориентации; если одна тройка является правой, а другая левой, то они называются тройками различной ориентации.
Замечание 2. При круговой перестановке векторов (первый заменяется вторым, второй третьим, третий первым) ориентация тройки не меняется, т. е. тройки a, b, c ; b, c, a и c, a, b имеют одну ориентацию. Если поменять местами два вектора, то ориентация
тройки меняется. Например, если a, b, c правая тройка, то тройка b, a, c тех же векторов будет левой.
Тройка векторов i, j, k, задающих декартову прямоугольную систему координат, является правой.
Определение 3. Векторным произведением векторов a и b называется вектор c,
обозначаемый c = a × b, удовлетворяющий условиям:
1) |
|
c |
= a |
|
|
|
|
|
|
|
|
|
sin( c |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
| · | |
b |
| · |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
| | |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c |
a, c b; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3) тройка |
|
|
|
|
|
|
|
|
|
правая (рис. 3). |
|
|
|
|
|
|||||||||||||||||||||||
a, |
|
|
b, |
c |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
× b |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
a |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b :H |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
ϕ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HH |
|
|
|
|
|
|
|
|
H |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HH |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
Hj |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 3
Из условия 1 следует, что модуль векторного произведения a × b равен площади S параллелограмма, построенного на векторах a и b , т. е.
S = a |
|
|
|
sin( c |
|
) = |
|
|
|
|
|
|
(6) |
|||
| · | |
b |
| · |
|
| |
|
× |
| |
|
||||||||
| |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a, b |
|
a |
|
b |
. |
|
||||
Равенство a × b = 0 выражает необходимое и достаточное условие коллинеарности двух векторов a и b ; в частности, для любого вектора a
|
× |
|
= 0. |
(7) |
a |
a |
5

Векторное произведение двух векторов обладает свойствами:
1)антиперестановочности множителей a × b = −b × a ;
2)сочетательности относительно скалярного множителя
(αa) × b = a × (αb) = α(a × b);
3) распределительности относительно сложения
(a + b) × c = a × c + b × c, c × (a + b) = c × a + c × b.
Замечание 3. Так как |i| = |j| = |k| = 1, i j, i k, j k и тройка i, j, k правая, то для орт координатных осей i, j, k справедливы следующие равенства:
i × j = k, j × i = −k; j × k = i, k × j = −i; k × i = j, i × k = −j;
i × i = 0, j × j = 0, k × k = 0.
Используя эти равенства, можно получить выражение координат векторного произведения через координаты сомножителей.
Рассмотрим векторы a = X1i + Y1j + Z1k и b = X2i + Y2j + Z2k, тогда
a × b = (X1i + Y1j + Z1k) × (X2i + Y2j + Z2k) = (по св-вам 2 и 3) =
= X1 · X2i × i + X1 · Y2i × j + X1 · Z2i × k+
+Y1 · X2j × i + Y1 · Y2j × j + Y1 · Z2j × k + Z1 · X2k × i+ +Z1 · Y2k × j + Z1 · Z2k × k = (по замечанию 3) =
=X1 · Y2k − X1 · Z2j − Y1 · X2k + Y1 · Z2i + +Z1 · X2j − Z1 · Y2i =
=(Y1 · Z2 − Z1 · Y2)i − (X1 · Z2 − Z1 · X2)j + (X1 · Y2 − Y1 · X2)k.
Полученный результат просто запомнить, если записать его в виде символического
определителя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1 |
Z1 |
|
|
|
|
X1 |
Z1 |
|
|
|
|
X1 |
Y1 |
|
|
|
|
|
b = |
|
|
|
|
|
|
|
|
|
= i |
|
|
+ k |
(8) |
|||||||||||||||||
|
a |
|
X1 |
Y1 |
Z1 |
|
j |
|||||||||||||||||||||||||||
|
|
× |
|
|
|
X2 |
Y2 |
Z2 |
|
|
|
|
Y2 |
Z2 |
|
− |
|
|
X2 |
Z2 |
|
|
|
|
X2 |
Y2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7.
Упростить выражение (3a − 2b) × (2a + 5b).
Решение. Пользуясь свойствами векторного произведения и формулой (7), получаем
(3a − 2b) × (2a + 5b) =
=(3a) × (2a) + (3a) × (5b) + (−2b) × (2a) + (−2b) × (5b) =
=6a × a + 15a × b − 4b × a − 15b × b = 15a × b + 4a × b = 19a × b.
Пример 8.
6

Даны векторы a, b, c, удовлетворяющие условию a + b + c = 0. Доказать, что a × b = b × c = c × a.
Решение. Умножим векторно a на a + b + c = 0. Получим
a × a + a × b + a × c = a × 0.
Откуда a × b + a × c = 0 , или a × b = −a × c = c × a.
Умножая векторно a + b + c = 0 на b, находим
a × b + b × b + c × b = 0 × b.
Откуда a × b + c × b = 0 , или a × b = −c × b = b × c.
Из двух равенств a × b = c × a и a × b = b × c следует доказываемое равенство
a × b = b × c = c × a.
Пример 9.
Вычислить площадь параллелограмма, построенного на векторах a и b, если a =
7p + q, b = p − 2q, |p| = 8, |q| = 5, ( c ) = |
6 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π . |
|
|
|
|
|
|
|
p, q |
||||||||||||
Решение. Пользуясь формулой (6), свойствами векторного произведения и условием коллинеарности векторов (7), имеем
S = |a × b| = |(7p + q) × (p − 2q)| = |7p × p + q × p − 14p × q − 2q × q| =
= |q × p + 14q × p| = |15q × p| = 15 |
· |q| · |p| · sin( c ) = |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p, q |
|||||
|
|
|
|
= 15 · 8 · 5 · sin |
|
π |
= 600 · |
1 |
|
= 300. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
6 |
2 |
|
|
|
|
|
||||||||||||||
Пример 10.
Даны векторы a = (1, −2, 2) , b = (3, 0, −4). Найти их векторное произведение, синус угла между ними и площадь параллелограмма, построенного на этих векторах.
Решение. Векторное произведение вычислим с помощью формулы (8):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
× |
|
b = |
|
1 2 2 |
|
|
|
= i |
|
− |
4 |
|
|
j |
3 |
|
|
|
|
|
4 |
|
+ k |
− |
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
3 0 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= i(8 − 0) − j(−4 − 6) + k(0 + 6) = 8i + 10j + 6k = (8, 10, 6). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
По формуле (6) находим площадь параллелограмма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
2 |
+ 10 |
2 |
+ 6 |
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
S = |a × b| = |
|
|
|
|
|
|
|
|
64 + 100 + 36 = |
|
|
|
|
200 = 10 2 . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Согласно условию 1 (определение 3), синус угла между данными векторами |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) = |
| |
|
|
|
|
× b| |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
sin( |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
a b |
|
|
|
|
p12 + ( 2)2 + 22 |
|
p32 |
+ 02 + ( 4)2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| · | |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
2 |
|
|
|
|
|
|
10 |
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
√ |
|
· |
√ |
|
= |
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 · 5 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 4 + 4 |
9 + 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Пример 11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(−1, 0, 2), |
B(1, −2, 5), |
||||||||||||||||||||
Вычислить площадь |
|
|
|
|
треугольника |
с |
вершинами |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C(3, 0, −4).
7
|
|
Решение. Находим |
сначала |
|
координаты |
|
|
векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
a |
|
= AB, |
|
b = AC : |
a |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2, −2, 3) , b = (4, 0, −6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Так как |
|
площадь |
|
|
треугольника |
|
|
ABC |
|
|
|
|
|
|
составляет |
половину |
площади |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
параллелограмма, построенного на векторах AB и AC , получаем S |
= |
|
| |
AB |
× |
AC |
| = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
21 | |
|
× b|. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Векторное произведение вычислим с помощью формулы (8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
× |
b = |
2 2 3 |
|
= i |
− |
|
|
6 |
|
|
|
|
j |
|
4 6 |
|
+ k |
|
− |
|
|
= |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
6 |
|
|
|
|
|
0 |
− |
− |
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
= i(12 − 0) − j(−12 − 12) + k(0 + 8) = 12i + 24j + |
8k = (12, 24, 8). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Откуда |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S = |
|
|
|a |
× b| = |
|
|
|
12 |
|
+ 24 |
|
+ 8 |
|
|
= |
|
|
144 + |
576 + 64 = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
=12 √784 = 12 · 28 = 14.
3.Смешанное произведение векторов
Определение 4. Смешанным произведением трех векторов a, b, c называется число (a×b, c), равное скалярному произведению вектора a×b (векторного произведения векторов a и b ) на вектор c.
Рис. 4
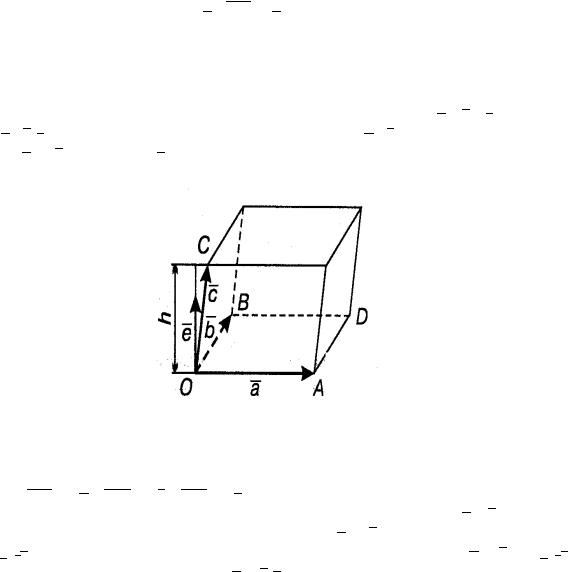
Пусть OA = a, OB = b, OC = c три некомпланарных вектора, образующих правую тройку. Построим на них параллелепипед (рис. 4). Поскольку |a × b| площадь параллелограмма OADB, построенного на векторах a и b , а по определению проекции h = прa×bc , получаем, что объем параллелепипеда V = SOADB · h = |a × b| · прa×bc = (по св-ву скалярного произведения) = (a × b, c).
8

В случае когда a, b, c образуют левую тройку, прa×bc < 0 и h = −прa×bc , откуда
V = |a × b| · (−прa×bc) = −(a × b, c) .
Обобщая все сказанное, получаем, что объем параллелепипеда, построенного на
векторах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b, c , равен модулю смешанного произведения этих векторов: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = |( |
|
× b, |
|
)|. |
|
|
|
|
|
|
(9) |
||
|
|
|
|
|
|
|
a |
c |
||||||||||||
|
Замечание 4. Объем треугольной пирамиды, построенной на векторах |
|
|
|
|
|
равен |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
a, b, c, |
|||||||||||||||||||
1 |
объема параллелепипеда, построенного на этих же векторах, т. е. |
|
||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = 16 |(a × b, c)|.
Если векторы a, b, c лежат в одной плоскости, то (a × b, c) = 0 , так как a × b перпендикулярен вектору c . Обратно, если (a × b, c) = 0 , то вектор c перпендикулярен вектору a × b и, следовательно, лежит в плоскости векторов a и b или в плоскости, параллельной этой плоскости. Таким образом, доказано следующее утверждение.
Утверждение 1. Необходимым и достаточным условием компланарности трех векторов a, b, c является равенство нулю их смешанного произведения:
|
|
|
|
|
|
|
|
( |
a |
× b, |
c |
) = 0. |
(10) |
||
Свойства смешанного произведения векторов:
1.(a × b, c) = (b × c, a) = (c × a, b) = −(b × a, c) = −(c × b, a) = −(a × c, b).
Это свойство позволяет ввести обозначение (a × b, c) = abc .
2.(a × (b + d), c) = (a × b, c) + (a × d, c);
(a × b, (c + d)) = (a × b, c) + (a × b, d).
3. (a × (αb), c) = (a × b, (αc)) = α(a × b, c), где α число.
Получим выражение смешанного произведения через координаты сомножителей.
Пусть a = (X1, Y1, Z1) , b = (X2, Y2, Z2) , c = (X3, Y3, Z3) . По формуле (8) имеем
a × b = (Y1 · Z2 − Y2 · Z1, X2 · Z1 − X1 · Z2, X1 · Y2 − X2 · Y1).
Используя формулу (3), получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
× b, |
|
) = |
|
|
||
|
|
a |
c |
|
|
|||||
= (Y1 · Z2 − Y2 · Z1) · X3 + (X2 · Z1 − X1 · Z2) · Y3 + (X1 · Y2 − X2 · Y1) · Z3 = |
|
|||||||||
|
|
X1 |
Y1 |
Z1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
X2 |
Y2 |
Z2 |
|
(11) |
||||
|
. |
|||||||||
|
|
X3 |
Y3 |
Z3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Пример 12.
Даны векторы a = (1, 3, 1), b = (−2, 4, −1), c = (2, 4, −6) . Требуется установить, компланарны ли данные векторы; в случае их некомпланарности выяснить, какую тройку (правую или левую) они образуют, вычислить объем построенного на них параллелепипеда.
9

Решение. Вычислим смешанное произведение векторов a, b, c по формуле (11):
|
|
|
|
|
|
|
|
1 |
3 |
1 |
|
|
|
|
|
|
|
|
|
(a |
|
b, c) = |
|
2 4 |
1 |
|
= 24 |
8 |
|
6 |
|
8 + 4 |
|
36 = 78. |
|||||
|
|
|
|
|
|
||||||||||||||
|
|
× |
|
|
|
|
|
− |
4 |
− |
|
− − |
|
− |
|
− |
|
− |
− |
|
|
|
|
|
|
|
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
Так как смешанное произведение не равно нулю, векторы a, b, c не компланарны; (a×b, c) < 0, значит a, b, c образуют левую тройку. По формуле (9) имеем V = |(a×b, c)| =
| − 78| = 78.
Пример 13.
Доказать, что точки A(3, −4, 1) , B(2, −3, 7) , C(1, −4, 3) , D(4, −3, 5) лежат в одной плоскости.
Решение. Если точки A, B, C и D лежат в одной плоскости, то векторы AB , AC
и AD также лежат в этой плоскости, а значит, являются компланарными.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB = (−1, 1, 6) |
, AC = (−2, 0, 2) , AD = (1, 1, 4) . Найдем их смешанное произведение: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
6 |
|
|
|
|
|
|
|
(AB |
|
|
AC, AD) = |
|
− |
|
2 |
|
= 0 + 2 |
|
12 |
|
0 + 2 + 8 = 0. |
|||||
|
|
|
|
2 0 |
|
|
|
||||||||||||
|
|
|
× |
|
|
|
|
|
|
− |
1 |
4 |
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как (AB × AC, AD) = 0 , то в силу утверждения 1 эти векторы компланарны. Что и требовалось доказать.
Пример 14.
Даны вершины пирамиды A(0, −2, 5) , B(6, 6, 0) , C(2, −1, 3) , D(3, −3, 6). Найти объем пирамиды и длину ее высоты, опущенной из вершины D .
Решение. Найдем координаты векторов AB , AC и AD, на которых построена пирамида ABCD :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B@ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B@ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B @ |
@ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-@ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
HH |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HHH B |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jHB |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
AB = (6, 8, −5) , AC = (2, 1, −2) , AD = (3, −1, 1). |
|
|
|
|
|
||||||||||||||||||||||||||
Вычислим их смешанное произведение: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
8 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(AB |
|
AC, AD) = |
|
2 |
1 |
|
− |
|
|
|
|
|
|
|
|
48 + 15 |
|
12 |
|
16 = 45. |
||||||||||
|
|
|
|
2 |
|
= 6 + 10 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
× |
|
|
|
|
|
|
|
3 |
1 |
|
− |
|
|
|
|
|
|
− |
|
− |
|
− |
− |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя формулу (9) и замечание 4, получаем |
|
|
|
|
||
Vпирамиды = |
1 |
| − 45| = |
45 |
= |
15 |
. |
|
|
|
||||
6 |
6 |
2 |
||||
10
