15

Модуль 1. Дифференциальное исчисление функции одной переменной

Тема 1. Функции одной переменной, свойства и графики

Функции одной переменной

1.1. Найти и построить область определения функций одной переменной.

а) ; б) ; в) ;

г) ; д) ; е) .

1.2. Установить, является ли функция четной или нечетной.

а) ; б) ; в) ; г) ,

д) ; е) .

1.3. По заданным функциям и построить сложную функцию

1.4. Построить графики функций с помощью геометрических преобразований графиков основных элементарных функций (сдвиг, растяжение и сжатие по осям).

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

11) ; 12) ;

13)

Тема 2. Предел функции

Вычисление предела

2.1. Вычислить пределы функций при .

1) ; 2) ; 3) ;

4) ; 5) ; 6) ; 7) .

2.2. Вычислить пределы функций при .

1); 2);

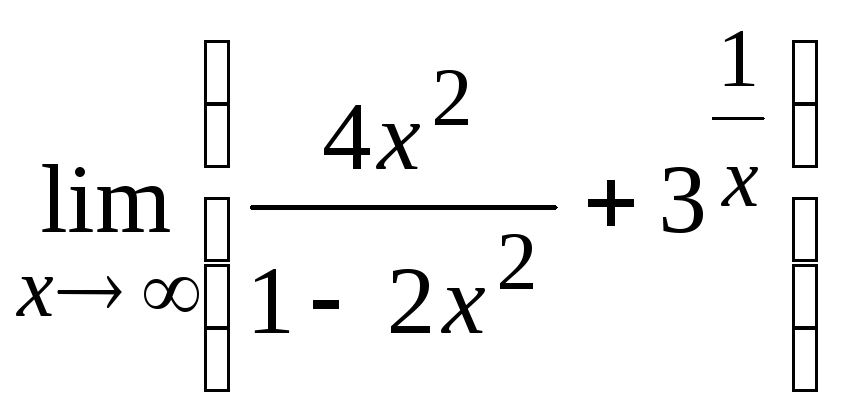3) ; 4).

Первый замечательный предел

2.3. Используя первый замечательный предел, вычислить пределы.

ж); з) ; и) .

Второй замечательный предел

2.3. Используя второй замечательный предел, вычислить пределы.

1) ; 2) ; 3) ;

4) ; 5) ; 6) .

Тема 3. Непрерывные функции

Точки разрыва функции

3.1. Найти точки разрыва функции

Непрерывность функции на отрезке

3.2. Исследовать на непрерывность функцию на отрезке:

Характер точек разрыва

3.3. Определить характер точек разрыва функции.

Тема 4. Производные и дифференциалы функции

Вычисление производных

4.1. Вычислить производные.

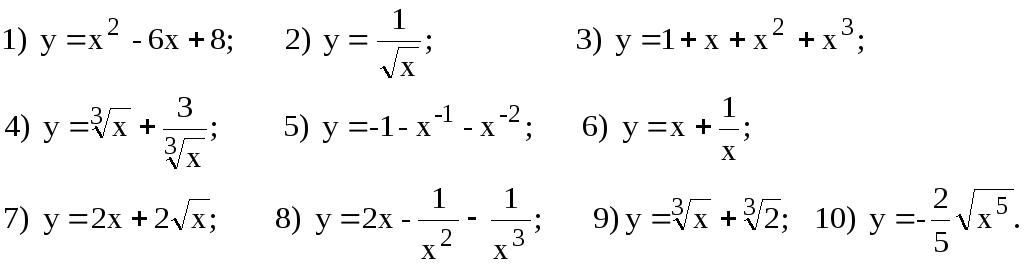
4.2. Вычислить производные.

Производные сложных функций

4.3. Пользуясь правилом дифференцирования сложной функции, найти производные функций.

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) .

Касательная к графику функции

4.4. Составить уравнения касательных к графикам функций:

1) y = x² - 3x + 2 в точке (3;2).

2) y = в точке (4;2).

3) y = ln x в точке пересечения с осью Оx.

4) y = x² - 5x + 6 в точках пересечения с осью Оx.

5) y = e^7x в точке пересечения с осью Оy.

Производные высших порядков

4.5. Найти производные 2-го порядка от функций:

1) ; 2) ; 3) ; 4) .

5.6. Найти производные n-го порядка от функций:

1) y = ; 2) y = e^2x; 3) y = 5^x; 4) y = ln(1+x).

Вычисление пределов с помощью производных (правило Лопиталя)

4.7. Найти пределы с помощью правила Лопиталя:

1) ; 2) ; 3) ; 4);

5) ; 6) ; 7)

Понятие дифференциала

4.8. Найти дифференциалы функций:

1) y = x³ – 3ln x; 2) y = ; 3) y = sin 3x; 4) y = tg ln x.;

5) y = x² arctg x; 6) y = ; 7) y = ; 8) y = .

4.9. Найти приближенно приращение у:

1) функции у = , если х = 4, х = 0,08;

2) функции у = sinx, если х = , х = 0,02.

Дифференциал второго порядка

4.10. Найти дифференциалы 2-го порядка от функций:

1) y = x³ – 3x² + x + 1; 2) y = (0,1x+1)⁵;

3) y = xcos2x; 4) y = sin²x.

Вычисление пределов с помощью производных (правило Лопиталя)

4.10. Найти пределы с помощью правила Лопиталя:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7)