4.4 Исследование работы интегратора напряжения.

Рисунок 15 – Электрическая схема для исследования работы интегратора напряжения

1. С помощью элементов управления ВП устанавливаем прямоугольную форму сигнала и частоту сигнала, равную 200 Гц. Амплитуда входного сигнала выбирается такой величины, при которой выходной сигнал не имеет искажений и удобен для наблюдения и измерений.

Рисунок 16 – График входного и выходного сигналов

2) Используя изображение выходного сигнала, определим скорость его изменения. Для этого измерим максимальное (u_mах) и минимальное (u_min) мгновенные значения сигнала и вычислим отношение размаха сигнала (u_max – u_min) к полупериоду его из­менения Т/2:

U_mах = 4,38 В U_min = -3,39 В.

∆Uвых / ∆t = 2*(4,38 - ( - 3,39)) / 0,005 = -3108

Рассчитаем скорость изменения выходного сиг­нала по значениям параметров компонентов схемы, используя формулу идеального интегратора:

∆Uвых / ∆t = - 0,5 / (10*10³*10*10^-9) = -3333,3

Скорость изменения выходного напряжения, вычисленная экспериментально, отличается от идеальной на 7%.

3) Получим осциллограммы выходного сигна­ла интегратора для синусоидальной, треугольной и пилообразной форм входного напряжения.

Рисунок 17 - Осциллограмма выходного сигна­ла интегратора для синусоидальной формы входного напряжения

Рисунок 18 - Осциллограмма для треугольной формы входного напряжения

Рисунок 19 - Осциллограмма для пилообразной формы входного напряжения

Вывод:

Интегратор напряжения интегрирует входное напряжение.

При синусоидальной форме входного сигнала, сдвиг фаз между входным и выходным сигналом составляет 90^о, т.к. интеграл синуса – минус косинус (выходной сигнал опережает входной на 90^о). Т.е. при синусоидальном входном сигнале на выходе получается косинусоидальный сигнал.

4.5 Исследование работы дифференциатора напряжения

Рисунок 20 – Электрическая схема для исследования работы дифференциатора напряжения

1) С помощью элементов управления ВП устанавливаем треугольную форму сигнала и частоту сигнала, равную 200 Гц. Амплитуда входного сигнала выбирается такой величины, при которой выходной сигнал не имеет искажений и удобен для наблюдения и измерений.

Рисунок 21 – График входного и выходного сигналов

2) Используя изображение выходного сигнала, определим его амплитуду U_ВЫХ.m в области установившегося значе­ния.

Uвых_mах = 6,71 В Uвых_min = -6,63 В.

Uвых _m = (Uвых_mах + Uвых_min ) / 2 Uвых _m = 6,67 В

3) Определим скорость изменения входного сигнала треугольной формы, используя для расчетов отношение удвоенной амплитуды входного сигнала (2U_m) к полупериоду изменения (Т/2) выход­ного напряжения:

∆Uвх / ∆t = 4*5,3 / 0,005

∆Uвх / ∆t = 4240

4) По заданным параметрам схемы и найденному значению скорости изменения входного сигнала рассчитаем амплитуду выход­ного напряжения по формуле идеального дифференциатора:

Uвых = -100000*15*10^-9 * 4240

Uвых = 6,36 В.

Сравним полученное значение с вычисленным в пункте 2. Отличие выходного напряжения данного реального дифференциатора от идеального составляет 5%.

5) Получим изображения сигнала на выходе дифференциатора напряжения для синусоидальной, прямоугольной и пило­образной форм входного напряжения.

Рисунок 22- Изображение сигнала на выходе дифференциатора напряжения для синусоидальной формы входного напряжения

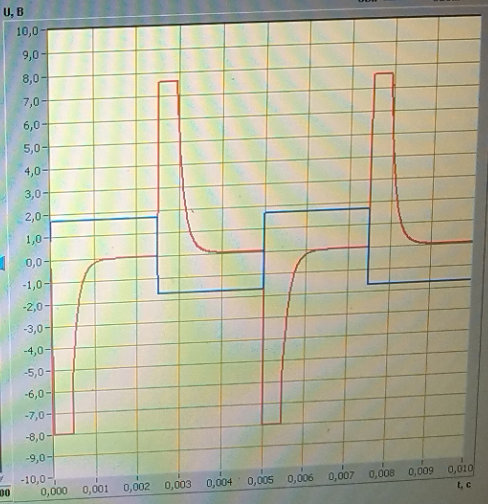
Рисунок 23- Изображение для прямоугольной формы входного напряжения

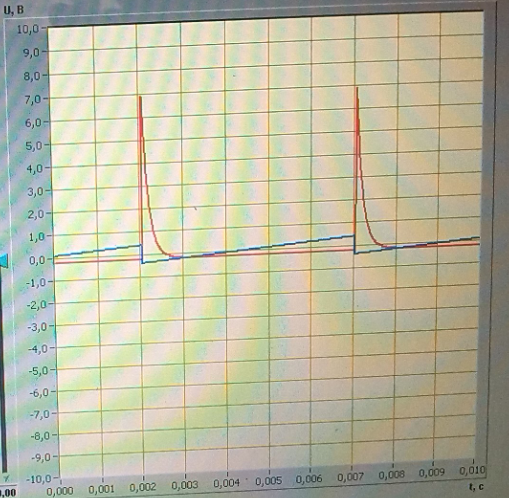
Рисунок 24- Изображение для пилообразной формы входного напряжения

Вывод:

Дифференциатор напряжения подаёт на выход дифференцированный входной сигнал.

При синусоидальной форме сигнала наблюдается сдвиг по фазе - выходной сигнал отстаёт от входного на 90^о. Т.к. производная (дифференциал) от синуса – косинус. Таким образом на выходе получим тоже косинусойду, как и у интегратора, но сдвиг будет происходить в другую сторону.

18