
- •Тема 1. Природа эконометрики
- •1.1. Общие понятия эконометрических моделей
- •1. 2. Типы эконометрических моделей
- •1. 3. Типы данных
- •Тема 2. Корреляционный анализ в эконометрических исследованиях
- •2.1. Функциональная, статистическая и корреляционная зависимости
- •2.2. Понятие о двумерном корреляционном анализе
- •2.3. Понятие о многомерном корреляционном анализе
- •2.4. Ранговая корреляция
- •Тема 3. Регрессионный анализ в эконометрических исследованиях
- •3.1. Задача регрессионного анализа
- •3.2. Идентификация модели регрессии
- •3.3. Линейная парная регрессия и оценка параметров
- •3.4. Проверка значимости параметров линейной парной регрессии
- •3.5. Интервалы прогноза по линейному уравнению регрессии
- •3.6. Нелинейная регрессия
- •3.7. Корреляционное отношение и индекс корреляции
- •3.8. Множественный регрессионный анализ
- •4.9. Ковариационная матрица и ее выборочная оценка
- •4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
- •4.11. Мультиколлинеарность
- •Тема 5. Методы и модели анализа динамики экономических процессов
- •5.1. Понятия экономических рядов динамики
- •5.2. Предварительный анализ динамических рядов экономических показателей
- •5.3. Сглаживание динамических рядов
- •4.3. Расчет показателей динамики развития эконометрических процессов
- •4.4. Тренд-сезонные экономические процессы и их анализ
- •Тема 5. Модели прогнозирования экономических процессов
- •5.7. Трендовые модели на основе кривых роста
- •5.2. Оценка адекватности и точности трендовых моделей
- •5.3. Прогнозирование экономической динамики на основе трендовых моделей
- •5.4. Адаптивные модели прогнозирования
- •Лучшая модель ар(1,1)
- •Характеристика остатков
- •Тема 8. Системы взаимозависимых эконометрических моделей
- •8.1. Особенности систем взаимозависимьех моделей
- •8.2. Формы представления систем взаимозависимых эконометрических моделей
- •8.3. Косвенный метод оценки коэффициентов структурной формы систем взаимозависимых эконометрических моделей
- •8.4. Оценивание параметров структурной формы на основе двухшагового мнк с использованием инструментальных переменных
- •1. На первом шаге конструируются новые значения зависимых
- •2. На втором шаге значения используются вместо значений
- •8.5. Оценки параметров системы взаимозависимых эконометрических моделей с использованием трехшагового мнк
8.5. Оценки параметров системы взаимозависимых эконометрических моделей с использованием трехшагового мнк
Как было отмечено в предыдущем разделе, наличие корреляционных связей между ошибками различных эконометрических моделей, входящих во взаимозависимую систему, ведет к потере свойства эффективности оценок их коэффициентов. В такой ситуации теория рекомендует для получения этих оценок вместо двух шагового использовать трехшаговый МНК, который включает в себя дополнительный этап, связанный с применением обобщенного МНК при известной ковариационной матрице ошибок различных моделей. В результате трехшаговый МНК применяется как метод оценивания коэффициентов структурной формы всей системы моделей, а не отдельных ее уравнений.
Дадим достаточно схематичное изложение трехшагового МНК в общем виде.
Представим
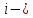 е
структурное уравнение системы в виде,
аналогичном (8.50),
е
структурное уравнение системы в виде,
аналогичном (8.50),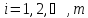 :
:
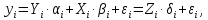 (8.70)
(8.70)
где,
как и в разделе 8.4,
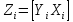 матрица,
сформированная на основе исходных
значений эндогенных и экзогенных
переменных
матрица,
сформированная на основе исходных
значений эндогенных и экзогенных
переменных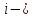 й
модели;
й
модели;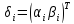 вектор
параметров
вектор
параметров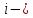 й
модели;
й
модели;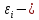 вектор
ошибки
вектор
ошибки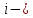 й
модели.
й
модели.
Умножим левую и правую части выражения (8.70) слева на транспонированную матрицу значений всех экзогенных переменных X. В результате получим модель следующего вида:
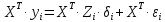 .
(8.71)
.
(8.71)
В
выражении (8.71) вектор
 рассматривается
как вектор значений новой зависимой
переменной, матрица
рассматривается
как вектор значений новой зависимой
переменной, матрица
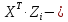 как
матрица значений новых независимых
факторов, а вектор
как
матрица значений новых независимых
факторов, а вектор как
вектор значений новой ошибки. При этом
ковариационная матрица этой ошибки
определяется согласно следующему
выражению:
как
вектор значений новой ошибки. При этом
ковариационная матрица этой ошибки
определяется согласно следующему
выражению:
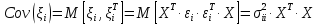 ,
(8.72)
,
(8.72)
где
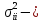 постоянная
дисперсия ошибки
постоянная
дисперсия ошибки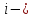 го
уравнения системы.
го
уравнения системы.
Поскольку
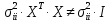 ,
т.е.
ковариационная матрица ошибки имеет
вид, отличный от единичной матрицы,
умноженной на постоянную дисперсию,
то для получения эффективных оценок
коэффициентов модели (8.71) необходимо
использовать обобщенный МНК. Оценка
,
т.е.
ковариационная матрица ошибки имеет
вид, отличный от единичной матрицы,
умноженной на постоянную дисперсию,
то для получения эффективных оценок
коэффициентов модели (8.71) необходимо
использовать обобщенный МНК. Оценка
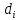 вектора
коэффициентов Si
в
этом случае определяется согласно
следующему выражению:
вектора
коэффициентов Si
в
этом случае определяется согласно
следующему выражению:
 .
(8.73)
.
(8.73)
С
учетом представления матрицы
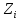 в
виде
в
виде
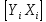 и
выражения (8.54) формула (8.73) тождественна
выражению (8.58).
и
выражения (8.54) формула (8.73) тождественна
выражению (8.58).
Применим преобразование (8.71) ко всей системе взаимозависимы уравнений, представленной в форме записи, аналогичной выражению (8.25). В результате получим следующую систему:
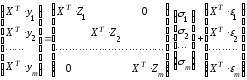 .
(8.74)
.
(8.74)
Ковариационная матрица вектора ошибки системы (8.74) будет иметь следующий вид:
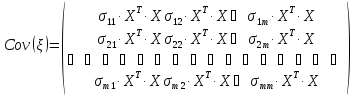 ,
(8.75)
,
(8.75)
где
символом
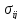 обозначена
ковариация ошибок
обозначена
ковариация ошибок
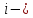 го
и
го
и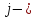 го
уравнений системы. Иными словами,
го
уравнений системы. Иными словами,
 .
(8.76)
.
(8.76)
Если
из значений
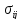 сформировать
матрицу
сформировать
матрицу
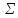 размера
размера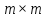 то
выражение (8.75) можно представить как
кронекерово произведение матриц
то
выражение (8.75) можно представить как
кронекерово произведение матриц
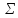 и
и
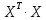 .
.
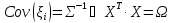 ,
(8.77)
,
(8.77)
где
символ
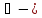 кронекерова
произведения.
кронекерова
произведения.
Согласно свойству кронекерова произведения,
 .
(6.78)
.
(6.78)
С учетом (8.78) оценку вектора коэффициентов всей системы взаимозависимых эконометрических моделей получим с использованием обобщенного МНК в следующем виде:
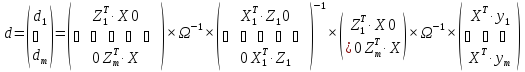 .
(6.79)
.
(6.79)
Таким образом, рассмотренная процедура оценки коэффициентов структурной формы всей системы взаимозависимых эконометрических моделей состоит из трех последовательных этапов, определяющих содержание трехшагового МНК.
Этап 1.
На
этом этапе с использованием обычного
МНК на основании приведенной формы
определяются расчетные значения
переменных
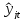 ,
рассматриваемых в качестве независимых
эндогенных переменных в каждом из
уравнений системы,
,
рассматриваемых в качестве независимых
эндогенных переменных в каждом из
уравнений системы,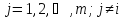 ,
где
,
где
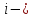 индекс
уравнения системы.
индекс
уравнения системы.
Этап 2.
Как
и в двухшаговом МНК, на этом этапе с
использованием значений
 определяются
оценки коэффициентов структурной формы
каждого из уравнений системы. Для этой
цели используется выражение (8.73).
определяются
оценки коэффициентов структурной формы
каждого из уравнений системы. Для этой
цели используется выражение (8.73).
Кроме
того, на этом шаге определяются векторы
ошибок каждого из уравнений системы
 с
использованием которых рассчитываются
на основании формулы (8.76) оценки дисперсии
каждого из уравнении
с
использованием которых рассчитываются
на основании формулы (8.76) оценки дисперсии
каждого из уравнении
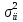 и
их взаимные ковариации
и
их взаимные ковариации
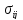 и
в соответствии с выражением (8.75)
формируется ковариационная матрица
и
в соответствии с выражением (8.75)
формируется ковариационная матрица
 .
.
Этап 3.
С помощью обобщенного МНК (выражение (8.79)) определяются «окончательные» оценки коэффициентов структурной формы всей системы взаимозависимых эконометрических моделей, которые теоретически при наличии корреляции между ошибками различных уравнений являются «более эффективными» по сравнению с аналогичными оценками двухшагового МНК.
Если
ошибки уравнений системы не коррелируют
между собой, т.е.
 ,
,
 ,
то
трехшаговый МНК не имеет преимуществ
перед двухшаговым. При применении
трехшагового МНК необходимо соблюдать
некоторые дополнительные правила,
что делает его процедуру менее
универсальной по сравнению с
двухшаговой. Они состоят в следующем:
,
то
трехшаговый МНК не имеет преимуществ
перед двухшаговым. При применении
трехшагового МНК необходимо соблюдать
некоторые дополнительные правила,
что делает его процедуру менее
универсальной по сравнению с
двухшаговой. Они состоят в следующем:
Процедура выполняется только для идентифицируемых и сверх-идентифицируемых уравнений системы. Тождества и неидентифицируемые уравнения в ней не участвуют.
Процедуру желательно выполнять для групп идентифицируемых и неидентифицируемых уравнений раздельно. При этом, если в соответствующую группу входит только одно сверхидентифицируемое уравнение, то трехшаговая процедура для него превращается в двухшаговую.
Наряду с рассмотренными в данном разделе методами существуют и некоторые другие, позволяющие получить «приемлемые по качеству» оценки коэффициентов структурной формы системы взаимозависимых эконометрических моделей. Так, эти оценки для отдельных моделей можно найти с помощью метода наименьшего дисперсионного отношения, в свою очередь базирующегося на методе максимального правдоподобия с ограниченной информацией, использующего, кроме обычных предположений с нормальности распределения и независимости ошибок структурного уравнения, также дополнительное предположение о ранге матрицы значений независимых переменных приведенной формы. Оценить коэффициенты структурной формы всей системы эконометрических моделей можно и на основе метода максимального правдоподобия с полной информацией.
Однако перечисленные методы гораздо более трудоемки по сравнению с двухшаговым и трехшаговым МНК , и, что самое главное, они не дают никаких преимуществ перед последними с точки зрения качества лученных оценок. Вследствие этого в большинстве эконометрических исследований, проводимых на основе систем взаимозависимых уравнений, для оценки их коэффициентов рекомендуется использовать именно двухшаговый и трехшаговый МНК.
ВОПРОСЫ К ГЛАВЕ VIII
1. Перечислите основные предпосылки систем взаимозависимых переменных.
2. Чем обусловлена смещенность оценок коэффициентов уравнений, полученных с использованием МНК?
3. Что представляют собой структурная и приведенная формы модели?
4. Как проводится оценивание коэффициентов с использованием ограничений на структурные параметры?
5. Что представляют собой порядковое и ранговое условия идентифицируемости уравнений структурной формы?
6. Что представляют собой рекурсивные системы моделей?
7. В чем состоит суть двухшагового и трехшагового МНК, используемых для оценки коэффициентов системы взаимозависимых уравнений?
УПРАЖНЕНИЯ К ГЛАВЕ VIII Задание 8.1
Имеется следующая модель:
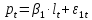 ;
(8.1)
;
(8.1)
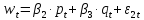 ;
(8.2)
;
(8.2)
 ,
(8.3)
,
(8.3)
где
 логарифм
цены;
логарифм
цены;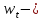 логарифм
почасовой оплаты,
логарифм
почасовой оплаты, логарифм
себестоимости;
логарифм
себестоимости;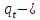 логарифм
объема производства и
логарифм
объема производства и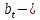 логарифм
количества рабочих часов в неделю в
период
логарифм
количества рабочих часов в неделю в
период .
.
Требуется:
Представить модель в матричной форме записи.
Определить ранговые условия идентифицируемости уравнений для
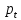 и
и
Задание 8.2
Имеется следующая макроэкономическая модель:
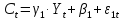 ;
(8.4)
;
(8.4)
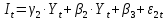 ;
(8.5)
;
(8.5)
 ,
(8.6)
,
(8.6)
где
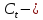 потребление;
потребление;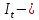 инвестиции,
инвестиции, государственные
расходы;
государственные
расходы;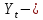 валовой
национальный продукт в период
валовой
национальный продукт в период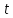 .
.
Требуется:
Определить типы уравнений и типы переменных, входящих в модель (8.4) – (8.6).
Представить структурные уравнения в матричной форме.
Построить соответствующую приведенную форму.
Определить метод оценки параметров приведенной формы.
Проверить идентифицируемость уравнений структурной формы модели.
Задание 8.3.
Имеется следующая система взаимозависимых уравнений:
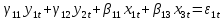 ;
;
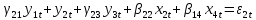 ;
;
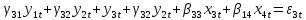 .
.
Проверить идентифицируемость уравнений системы.
Выяснить идентифицируемость, если на параметры наложены еле дующие ограничения:
а)
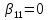 ;
;
б)
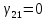 .
.
Задание 8.4
Имеется следующая макроэкономическая модель:
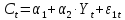 ;
;
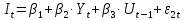 ;
;
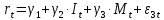 ;
;
 .
.
Требуется описать процедуру оценивания уравнений по двухшаговому МНК.
Задание 8.5
Имеется следующая макроэкономическая модель:
 ;
;
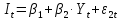 ;
;
 .
.
Требуется:
Написать модель в матричном виде и найти соответствующую прогнозную форму.
Определить число ограничений, наложенных на коэффициенты приведенной формы.
Показать, что при заданных значениях коэффициентов приведенной формы можно однозначно определить коэффициенты структурной формы.
