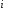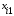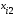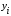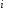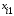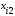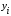- •Тема 1. Природа эконометрики
- •1.1. Общие понятия эконометрических моделей
- •1. 2. Типы эконометрических моделей
- •1. 3. Типы данных
- •Тема 2. Корреляционный анализ в эконометрических исследованиях
- •2.1. Функциональная, статистическая и корреляционная зависимости
- •2.2. Понятие о двумерном корреляционном анализе
- •2.3. Понятие о многомерном корреляционном анализе
- •2.4. Ранговая корреляция
- •Тема 3. Регрессионный анализ в эконометрических исследованиях
- •3.1. Задача регрессионного анализа
- •3.2. Идентификация модели регрессии
- •3.3. Линейная парная регрессия и оценка параметров
- •3.4. Проверка значимости параметров линейной парной регрессии
- •3.5. Интервалы прогноза по линейному уравнению регрессии
- •3.6. Нелинейная регрессия
- •3.7. Корреляционное отношение и индекс корреляции
- •3.8. Множественный регрессионный анализ
- •4.9. Ковариационная матрица и ее выборочная оценка
- •4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
- •4.11. Мультиколлинеарность
- •Тема 5. Методы и модели анализа динамики экономических процессов
- •5.1. Понятия экономических рядов динамики
- •5.2. Предварительный анализ динамических рядов экономических показателей
- •5.3. Сглаживание динамических рядов
- •4.3. Расчет показателей динамики развития эконометрических процессов
- •4.4. Тренд-сезонные экономические процессы и их анализ
- •Тема 5. Модели прогнозирования экономических процессов
- •5.7. Трендовые модели на основе кривых роста
- •5.2. Оценка адекватности и точности трендовых моделей
- •5.3. Прогнозирование экономической динамики на основе трендовых моделей
- •5.4. Адаптивные модели прогнозирования
- •Лучшая модель ар(1,1)
- •Характеристика остатков
- •Тема 8. Системы взаимозависимых эконометрических моделей
- •8.1. Особенности систем взаимозависимьех моделей
- •8.2. Формы представления систем взаимозависимых эконометрических моделей
- •8.3. Косвенный метод оценки коэффициентов структурной формы систем взаимозависимых эконометрических моделей
- •8.4. Оценивание параметров структурной формы на основе двухшагового мнк с использованием инструментальных переменных
- •1. На первом шаге конструируются новые значения зависимых
- •2. На втором шаге значения используются вместо значений
- •8.5. Оценки параметров системы взаимозависимых эконометрических моделей с использованием трехшагового мнк
3.8. Множественный регрессионный анализ
Экономические
явления, как правило, определяются
большим числом одновременно и
совокупно действующих факторов. В связи
с этим часто возникает задача исследования
зависимости одной зависимой переменной
Y
от нескольких объясняющих переменных
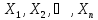 .
Эта задача решается с помощьюмножественного
регрессионного анализа.
.
Эта задача решается с помощьюмножественного
регрессионного анализа.
Множественное линейное уравнение регрессии имеет вид:
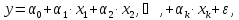 (3.49)
(3.49)
где
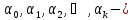 неизвестные
параметры модели;
неизвестные
параметры модели;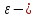 случайная
ошибка модели, обусловленная
влиянием неучтенных факторов в модель,
а также случайными ошибками наблюдении.
случайная
ошибка модели, обусловленная
влиянием неучтенных факторов в модель,
а также случайными ошибками наблюдении.
Для определения неизвестных параметров модели множественной регрессии из генеральных совокупностей сформированы две выборки объемами n:
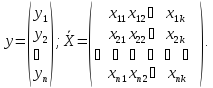
Подставляя эти выборки в модель регрессии (3.49) получим систему уравнении множественной линейной регрессии:
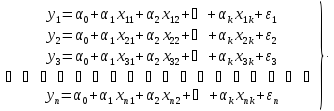 (3.50)
(3.50)
Включение в регрессионную модель новых объясняющих переменных (факторов) усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.
Введем
обозначения:
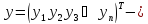 вектор
столбец, значений зависимой переменной
размера
n;
вектор
столбец, значений зависимой переменной
размера
n;

— матрица
значений объясняющих переменных,
или
матрица
плана
размера
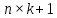 ;
;
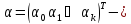 вектор
столбец,
параметров
размера
(k+1);
вектор
столбец,
параметров
размера
(k+1);
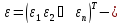 вектор
столбец,
возмущений
(случайных
ошибок, остатков)
размера п.
вектор
столбец,
возмущений
(случайных
ошибок, остатков)
размера п.
Тогда в матричной форме модель (3.50) примет вид:
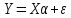 .
(3.51)
.
(3.51)
Оценкой этой модели по выборке является уравнение
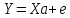 ,
(3.52)
,
(3.52)
где
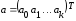 ,
,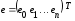 .
.
Для
оценки вектора неизвестных параметров
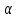 применимметод
наименьших квадратов. Так
как произведение транспонированной
матрицы
применимметод
наименьших квадратов. Так
как произведение транспонированной
матрицы
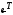 на саму матрицу
на саму матрицу
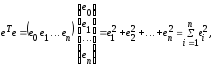
то условие минимизации остаточной суммы квадратов запишется в виде:
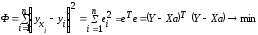 .
(3.53)
.
(3.53)
Учитывая,
что при транспонировании произведения
матриц получается произведение
транспонированных матриц, взятых в
обратном порядке, т.е.
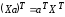 ,
получим
после раскрытия скобок:
,
получим
после раскрытия скобок:
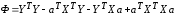 .
(3.54)
.
(3.54)
Произведение
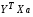 есть
матрица размера
есть
матрица размера
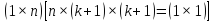 ,
т.е. величина скалярная, следовательно,
оно не меняется при транспонировании:
,
т.е. величина скалярная, следовательно,
оно не меняется при транспонировании: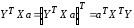 .
Поэтому
условие минимизации (3.54)
примет
вид:
.
Поэтому
условие минимизации (3.54)
примет
вид:
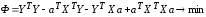 .
.
На
основании необходимого условия экстремума
функции нескольких переменных
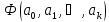 ,
представляющей(3.55),
необходимо
приравнять к нулю частные производные
по этим переменным или в матричной
форме — вектор частных производных
,
представляющей(3.55),
необходимо
приравнять к нулю частные производные
по этим переменным или в матричной
форме — вектор частных производных
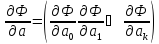 .
(3.55)
.
(3.55)
Таким образом,
встает задача найти минимум этой функций.
Для этого выражение (3.55) следует
продифференцировать по векторному
аргументу
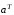 и полученное выражение приравнять к
нулю, то есть:
и полученное выражение приравнять к
нулю, то есть:
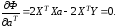
Отсюда получается следующее выражение:
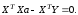
Данная система
уравнений называется нормальной системой
уравнений регрессии. Требуется ввести
обозначения:
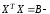 матрица
коэффициентов нормальных уравнений,
матрица
коэффициентов нормальных уравнений,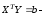 вектор-столбец
свободных членов нормальных уравнений
регрессии.
вектор-столбец
свободных членов нормальных уравнений
регрессии.
С учетом введенных обозначений нормальная система уравнений регрессии перепишется в окончательном виде:
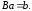 (3.56)
(3.56)
Для
решения матричного уравнения (3.56)
относительно
вектора оценок параметров
 необходимо
ввести предпосылку
для
множественного регрессионного анализа:
матрица
необходимо
ввести предпосылку
для
множественного регрессионного анализа:
матрица
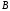 является неособенной,т.е.
ее определитель не равен нулю.
Следовательно, ранг матрицы
является неособенной,т.е.
ее определитель не равен нулю.
Следовательно, ранг матрицы
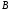 равен
ее порядку, т.е.
равен
ее порядку, т.е.
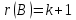 .
Из
матричной алгебры известно, что
.
Из
матричной алгебры известно, что
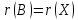 ,
значит,
,
значит,
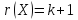 ,
т.е.
ранг матрицы плана
,
т.е.
ранг матрицы плана
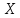 равен
числу ее столбцов.
равен
числу ее столбцов.
Кроме
того, полагают, что число имеющихся
наблюдений (значений) каждой из объясняющих
переменных превосходит ранг матрицы
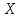 ,
т.е.
,
т.е.
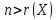 или
или
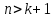 ,
ибо в противном случае в принципе
невозможно получение сколько-нибудь
надежных статистических выводов.
,
ибо в противном случае в принципе
невозможно получение сколько-нибудь
надежных статистических выводов.
Если матрица
коэффициентов нормальных уравнений
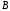 хорошо обусловлена и обратима, то можно
получить решение системы (3.56), например,
в виде:
хорошо обусловлена и обратима, то можно
получить решение системы (3.56), например,
в виде:
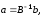 (3.57)
(3.57)
где
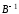 - обратная матрица, соответствующая
условиям:
- обратная матрица, соответствующая
условиям:
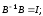
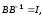
где
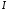 - единичная матрица соответствующих
размеров.
- единичная матрица соответствующих
размеров.
Зная
вектор ,
модель
уравнения множественной регрессии
можно представить в виде:
,
модель
уравнения множественной регрессии
можно представить в виде:
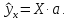 (3.58)
(3.58)
Преобразуем вектор оценок (13.26) с учетом (13.23) получим:
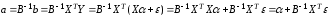 ,
,
Откуда
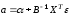 ,
(3.59)
,
(3.59)
т. е. оценки параметров (3.59), найденные по выборке, будут содержать случайные ошибки.
Пример 13.4. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего Y(t), мощности пласта Х\ (м) и уровне механизации работ Х2 (%), характеризующие процесс добычи угля в 10 шахтах.
Таблица 13.6
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 |
8 11 12 9 8 |
5 8 8 5 7 |
5 10 10 7 5 |
6 7 8 9 10 |
8 9 9 8 12 |
8 6 4 5 7 |
6 6 5 6 8 |
Предполагая,
что между переменными
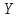 ,
,
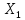 и
и
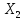 существует
линейная корреляционная зависимость,
найти ее аналитическое выражение
(уравнение регрессии
существует
линейная корреляционная зависимость,
найти ее аналитическое выражение
(уравнение регрессии
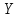 ,
по
,
по
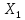 и
и
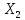 .
.
Решение. Обозначим
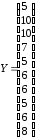 ,
,
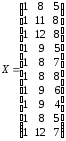 ,
,

(напоминаем, что в матрицу плана X вводится дополнительный столбец чисел, состоящий из единиц).
Решение системы уравнении найдем методом псевдонормального решения:
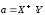 ,
(3.60)
,
(3.60)
где
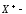 псевдообратная
матрица к исходной матрице
псевдообратная
матрица к исходной матрице
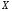 .
.
Псевдообратную матрицу найдем по рекурсивному алгоритму (№№№) и она равна:

Тогда по формуле (13.29) найдем вектор столбец параметров регрессии:
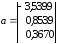 .
.
С учетом (13.27) уравнение множественной регрессии имеет вид:
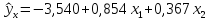 .
(13.30)
.
(13.30)
Уравнение
множественной регрессии (13.30) показывает,
что при увеличении только мощности
пласта
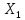 (при
неизменном
(при
неизменном
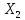 )
на
1 м, добыча угля на одного рабочего Y
увеличивается
в среднем на 0,854 т, а при увеличении
только уровня механизации работ
)
на
1 м, добыча угля на одного рабочего Y
увеличивается
в среднем на 0,854 т, а при увеличении
только уровня механизации работ
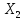 на
1%
(при
неизменной
на
1%
(при
неизменной
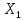 )
в среднем на 0,367 т.
)
в среднем на 0,367 т.
Добавление
в регрессионную модель новой объясняющей
переменной
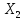 изменило
коэффициент регрессии
изменило
коэффициент регрессии
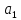 (Y
по
(Y
по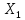 )
с
1,016 для парной регрессии (см.
пример 13.1)
до
0,854 — для множественной регрессии. В
этом никакого противоречия нет, так как
во втором случае коэффициент регрессии
позволяет оценить прирост зависимой
переменной Y
при
изменении на единицу объясняющей
переменной
)
с
1,016 для парной регрессии (см.
пример 13.1)
до
0,854 — для множественной регрессии. В
этом никакого противоречия нет, так как
во втором случае коэффициент регрессии
позволяет оценить прирост зависимой
переменной Y
при
изменении на единицу объясняющей
переменной
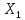 в
чистом виде, независимо от
в
чистом виде, независимо от
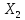 .
В
случае парной регрессии
.
В
случае парной регрессии
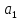 учитывает
воздействие на Y
не
только переменной
учитывает
воздействие на Y
не
только переменной
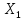 ,
но
и косвенно корреляционно связанной с
ней переменной
,
но
и косвенно корреляционно связанной с
ней переменной
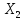 .
►
.
►
На
практике часто бывает необходимо
сравнение влияния на зависимую переменную
различных объясняющих переменных, когда
последние выражаются разными единицами
измерения. В этом случае используют
стандартизованные
коэффициенты регрессии
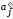 и
коэффициенты
эластичности
и
коэффициенты
эластичности
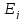 :
:
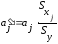 .
(13.31)
.
(13.31)
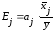 .
(13.32)
.
(13.32)
Стандартизованный
коэффициент регрессии
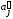 показывает,
на сколько величин
показывает,
на сколько величин
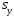 изменится в среднем зависимая переменнаяY
при увеличении только j-й
объясняющей переменной на
изменится в среднем зависимая переменнаяY
при увеличении только j-й
объясняющей переменной на
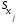 ,
а коэффициент эластичности
,
а коэффициент эластичности
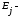 на
сколько процентов (от
средней)
изменится в среднем Y
при увеличении только
на
сколько процентов (от
средней)
изменится в среднем Y
при увеличении только
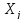 на 1%.
на 1%.