
Kolloidnaya_khimia_2
.pdf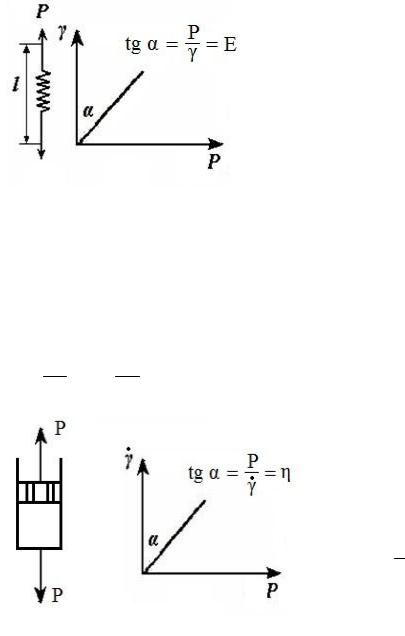
Идеально упругое тело Гука
Модель – спиральная пружина (рис. 47). В соответствии с законом Гука деформация в упругом теле пропорциональна напряжению
сдвига |
P |
или P E , где E |
– модуль Юнга, Па . |
|||
E |
||||||
|
|
|
|
|
||
|
|
|
|
|
Модуль Юнга является характе- |
|
|
|
|
|
|
ристикой материала, количественно |
|
|
|
|
|
|
отражающей его упругие свойства |
|
|
|
|
|
|
(жесткость). |
|
|
|
|
|
|
После снятия нагрузки идеально |
|
|
|
|
|
|
упругое тело Гука мгновенно (со ско- |
|
|
|
|
|
|
ростью распространения в нем звука) |
|
|
|
|
|
|
переходит в первоначальное состоя- |
|
|
|
Рис. 47 |
|
|||
|
|
|
ние. |
|||
|
|
|
|
|
|
|
Идеально вязкое тело Ньютона
Модель – поршень с отверстиями, помещенный в цилиндр с жидкостью (рис. 48). Идеально вязкая жидкость течет в соответствии с законом Ньютона: напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости
P dUdx , где dUdx – скорость деформации сдвига.
Закон Ньютона: напряжение сдвига пропорционально скорости деформации P .
Реологические свойства идеальных жидкостей однозначно характеризуются вязко-
стью. 1 – текучесть. Вязкость
характеризует сопротивление Рис. 48 жидкости движению, а теку-
честь – ее подвижность.
, Па с . 1Па с 10П (Пуаз) . Вязкость воды при 20,5 °C 1П или 0,001
Па с .
Величина деформации жидкости зависит от времени действия
|
P |
или |
d |
|
P |
, то |
P |
. |
напряжения, т.к. |
|
d |
|
|
||||
|
|
|
|
|
|
73 |
|
|
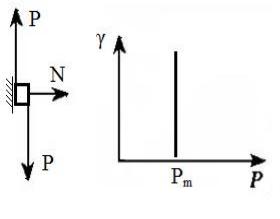
Идеально пластическое тело Сен-Венана – Кулона
Модель – твердое тело, находящееся на плоскости, при движении которого трение постоянно и не зависит от нормальной силы (рис. 49). В основе модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Pm , называемой пределом теку-
чести, т.е. при P Pm 0 , 0 .
Если напряжение достигает предела текучести P Pm , то разви-
ваемая деформация идеально пластического тела не имеет предела, и течение происходит с любой скоростью, т.е. 0 , 0 .
К идеально пластическому телу не может быть приложено напряжение, превышающее Pm . Эта
величина отражает прочность структуры тела. При P Pm струк-
тура разрушается и сопротивление напряжению полностью отсутствует. Из сравнения идеальных эле-
Рис. 49 ментов следует, что энергия, затраченная на диффузию упругого тела при разгрузке возвращается (система консервативна), а при деформации вязкого и пластического тел она превращается в теплоту, рассеивается (система диссипативна).
Моделирование реологических свойств тел
Многообразные реологические свойства реальных тел можно моделировать с помощью различных сочетаний идеальных моделей. Сложные модели состоят из нескольких идеальных элементов, соединенных между собой последовательно или параллельно. При последовательном соединении элементов полная нагрузка P приходится на каждый элемент, а полная деформация или ее скорость складывает-
ся: P P |
P ... |
P |
; |
|
1 |
|
2 |
... |
n |
|
|
|
|
|
|
1 |
2 |
m |
|
|
|
|
|
одинаковы для |
|||||
|
При параллельном соединении элементов и |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
всех |
элементов, а полная нагрузка |
складывается: |
P P P |
... P |
; |
|||||||||
1 |
2 |
... n |
; 1 2 |
... n . |
|
|
1 2 |
n |
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
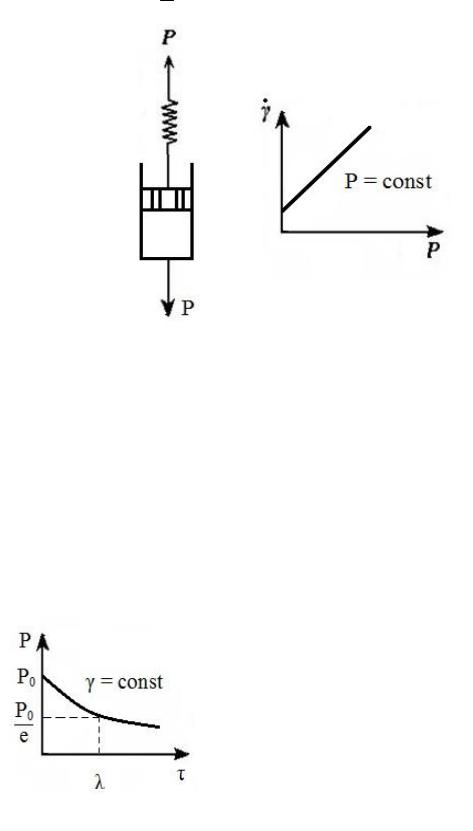
Модель Максвелла
Элемент Гука и Ньютона соединены последовательно (рис. 50):
P PГ
Г EP ;
P |
; |
|
|
|
; |
|
d |
|
|
d Г |
|
|
d Н |
|
|
|||||||||
|
|
|
d |
|
d |
|
d |
|
|
|||||||||||||||
|
Н |
|
|
|
Г |
|
|
Н |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
P |
; |
|
P |
|
P |
|
и |
d |
|
1 |
|
dP |
|
P |
|||||||
|
Н |
|
|
|
|
|
E |
|
|
|
|
|
|
d |
E d |
|
||||||||
Рис. 50
Это математическое выражение модели Максвелла – упруго вязкого тела. Наиболее интересна эта модель для мгновенной и фиксированной деформации ( const ; 0 ). Это состояние реализуется при мгновенном растяжении модели с сохранением в дальнейшем постоянной деформации. При этом возникшее внутреннее напряжение постепенно снижается со временем (релаксирует) вследствие деформирования вязкого элемента (рис. 51).
|
|
|
1 |
|
dP |
|
P |
|
0 и |
|
dP |
|
|
E |
d |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
E d |
|
|
|
P |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
dP |
|
|
|
E |
d ; |
|
P |
|
|
|
E |
|
|
, |
|||||||
|
ln |
|
|
|
; P P e |
|||||||||||||||||
|
|
P |
|
|||||||||||||||||||
P0 P |
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
где |
|
– время релаксации напряжения, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
это время, в течение котрого P0 в теле |
||||||||||||||
|
|
|
|
|
|
|
|
уменьшается в e раз. Чем больше , тем |
||||||||||||||
|
|
|
|
|
|
|
|
медленнее рассасывается (релаксирует) на- |
||||||||||||||
|
|
|
|
|
|
|
|
пряжение в системе. Явление релаксации, |
||||||||||||||
|
|
|
|
|
|
|
|
как и процесс диффузии, связано с тепло- |
||||||||||||||
|
|
|
|
|
|
|
вым движением молекул или частиц дис- |
|||||||||||||||
Рис. 51 |
|
|
|
|
|
персной фазы. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
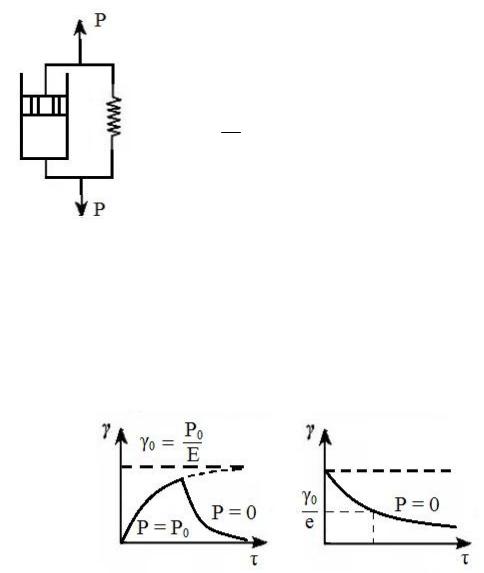
Различие между жидкостями и твердыми телами не является
резким и носит кинетический |
(релаксационный) характер. Если |
– тело твердое, если |
– тело ведет себя как жидкость: на- |
пряжения уменьшаются благодаря ее течению.
Модель Кельвина – Фойгта
Элементы Гука и Ньютона соединены параллельно (рис. 52):
P PГ PН , т.е. |
|
, т.к. PГ |
Г E , а PН |
|
H |
|
|
|
|||||||
P E |
. |
Деформация в таком теле под действием постоянной нагрузки развивается во времени. Скорость ее снижается т.к. элемент Гука испытывает все большее напряжение. При 0 деформация достигает максимального значения:
d
d
|
где |
|
|
|
Рис. 52 |
||||
E |
|
P |
|
E |
|
P |
|
|
|
E |
|
|
|
0 |
|
|
; |
0 |
1 |
exp |
|
|
|
или |
|
|
|
|
||||||||
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 |
|
|
|
|
, |
|
|
|
1 |
exp |
|
|
|
|
|
|
||||||
|
E |
|
|
|
|
|
|
|
|
|
|
|
|||
– время релаксации деформации при
постоянной нагрузке, характеризующее эластич-
ность тела.
Если напряжение после достижения определенной деформации, то система возвращается в исходное состояние в течение какого-то
времени (рис. 53). В этом случае |
|
и |
|
|
|
E |
|
|
|
|
|
|
. |
|
P 0 |
0 |
exp |
|
|
|
|
0 |
exp |
|
|
|
|||
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Чем больше , тем больше эластичность тела.
Рис. 53
Гуковские деформации твердых тел не превышают 0,1 %, а эластические могут достигать сотни % (каучуки, резина). Эластическая деформация имеет энтропийный характер.
76
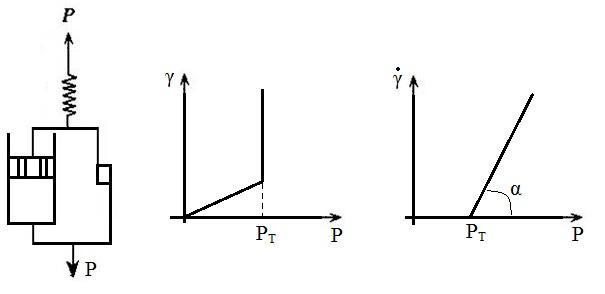
Модель Бингама
Элементы Ньютона и Сен-Венана – Кулона соединены параллельно, а элемент Гука последовательно к ним (рис. 54).
В этой модели при малых напряжениях развиваются только упругие деформации, а при достижении P PT имеет место пластиче-
ская деформация, растущая до бесконечности (течение вязкопластического тела).
Математическая модель.
P PT ПЛ , где ПЛ – пластическая вязкость.
0 |
при P PT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При PT 0 |
имеем закон Ньютона. ПЛ отличается от H |
||||||||||
|
|
|
|
PT |
ПЛ |
|
|
|
PT |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
ПЛ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
H учитывает все виды сопротивления течению тела, а ПЛ не
учитывает прочность структуры, но отражает скорость ее разрушения.
Рис. 54
При PT 0 P ПЛ соотношение переходит в закон Ньютона. Напряжение P разбивается как бы на две составляющие: PT , необходимое для разрушения структуры и напряжение P PT , осуществляющее собственное течение.
77
11.3. Классификация дисперсных систем по структурномеханическим свойствам.
Анализ многообразных свойств структур в дисперсных системах позволил Ребиндеру разделить их на два основных класса, различающихся по видам взаимодействия частиц дисперсной фазы. Исходя из того, что коагуляция соответствует первичному и вторичному минимуму потенциальной кривой взаимодействия частиц, он предложил различать конденсационно-кристаллизационные и коагуляционные структуры. Первые образуются в первичном потенциальном минимуме путем непосредственного химического взаимодействия между частицами и их срастанием при формировании жесткой объемной структуры. Если частицы аморфные – конденсационные структуры, если частицы кристаллические – кристаллизационные структуры. Конден- сационно-кристаллизационные структуры типичны для связнодисперсных систем. Такие структуры предают телам прочность, хрупкость и не восстанавливаются после разрушения.
Коагуляционные структуры образуются при коагуляции во вторичном минимуме потенциальной кривой через прослойку дисперсной среды между частицами, поэтому пространственный каркас такой структуры не отличается высокой прочностью. Для нее характерна способность восстанавливать структуру во времени после ее механического разрушения. Это явление называется тиксотропия.
Все реальные тела делят на жидкообразные ( PT 0 ) и твердообразные ( PT 0 ).
Жидкообразные классифицируют на ньютоновские и неньютоновские жидкости. Ньютоновскими жидкостями называют системы, вязкость которых не зависит от напряжения сдвига и являются величиной постоянной в соответствии с законом Ньютона. Для неньютоновских жидкостей все наоборот. Они подразделяются на стационарные, реологические свойства которых не изменяются во времени, и нестационарные. Среди неньютоновских стационарных жидкостей различают псевдопластические и дилатантные.
Разбавленные дисперсные системы с ровноосными частицами обычно ньютоновские жидкости. К псевдопластическим относятся суспензии, содержащие ассиметричные частицы, и растворы полимеров. Дилатантное поведение наблюдается у дисперсных систем с большим содержанием твердой фазы (керамические массы). Реологические кривые или кривые течения представлены на рис. 55
78
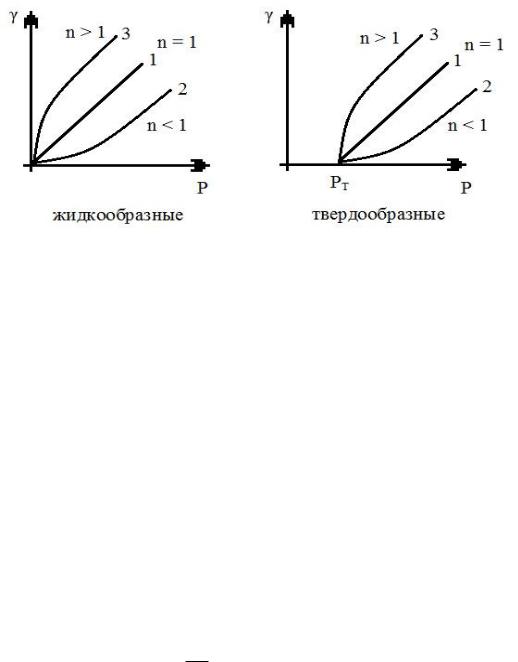
Рис. 55
1.Ньютоновские жидкости или тела бингама
2.Псевдопластические жидкости или тела
3.Дилатантные
Зависимость напряжения сдвига от скорости деформации: P k n для жидкообразных систем. Это математическая модель Ост-
вальда – Вейля. |
|
P |
|
n 1 |
– ньютоновская вязкость неньютонов- |
||
|
|
||||||
|
k |
||||||
|
|
|
|
|
|
|
|
ской стационарной жидкости. |
Если |
n 1, жидкость ньютоновская и |
|||||
n k . Т.о. отклонение |
n от |
1 характеризует степень |
отклонения |
||||
свойств жидкости от ньютоновских. |
|
|
|||||
Твердообразные системы подразделяются на бингамовские и |
|||||||
небингамовские. |
|
Их |
поведение |
описывается |
уравнением: |
||
P PT k n .
По реологическим свойствам к бингамовским твердообразным системам близки пульпы, масляные краски, зубные пасты. Их часто относят к неньютоновсим жидкостям.
dU
Закон Ньютона P dx интегрируя это уравнение может быть
получено уравнение Пуазейля: V |
r 4 P |
, |
|
|
|||||
8 l |
|
|
|||||||
|
|
|
|
|
|
|
|
||
где V объем |
жидкости, |
вытекающий |
за время из |
трубки |
|||||
радиусом r ; |
|
|
|
|
|
|
|
|
|
P – разность давлений на обоих концах трубки; |
|
||||||||
– вязкость жидкости; |
|
|
|
|
|
||||
l – длина трубки. |
|
|
|
|
|
||||
При малых |
P и |
dU |
|
наблюдается линейный характер, |
то есть |
||||
dx |
|||||||||
|
|
|
|
|
|
|
|||
неньютоновская |
жидкость |
течет |
подобно |
ньютоновской, но имеет |
|||||
79
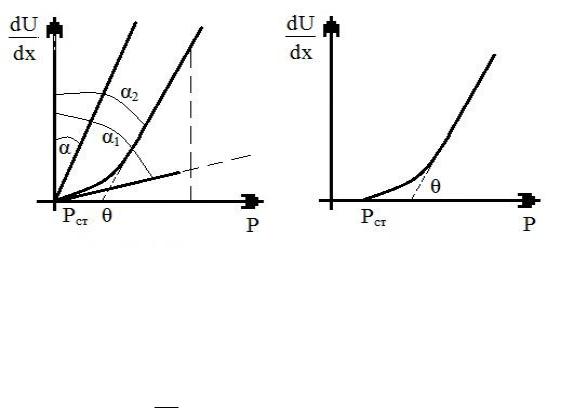
очень большую вязкость tan 1. Течение происходит без разрушения структуры и называется ползучестью PСТ – статическое предельное напряжение сдвига (рис. 56).
Рис. 56
Вдальнейшем повышение P вызывает разрушение структуры и
непрерывно уменьшается. При достижении PМ структура полно-
стью разрушается и минимальна tan 2 . PМ – предельное напряжение сдвига . Уравнение Бингама для течения неньютоновских
жидкостей: P Q ' dUdx ,
где Q – предельное динамическое напряжение сдвига;
' – пластическая вязкость.
Кявлению, противоположному тиксотропии, относится реопексия – возрастание прочности структуры (вязкости) со временем при действии напряжения сдвига.
11.4. Реологические свойства дисперсных систем
Вязкость
Основы теории вязкости разбавленных лиозолей (суспензий) были заложены Эйнштейном. Уравнение Эйнштейна:
0 (1 2,5 ) ,
где 0 – вязкость среды;
– объемная доля дисперсной фазы;
– вязкость системы.
80

При выводе предполагалось, что система несжимаема, отсутствует скольжение между частицами и жидкостью, а также турбулентность и взаимодействие между частицами.
0 1 ,
где α коэффициент формы частиц, 2,5 для сферических частиц и
2,5 , для частиц несферической формы.
1
отн 0
|
|
|
0 |
|
|
1 |
|
уд |
0 |
отн |
|||||
|
|
|
|
||||
|
|
|
|
|
|
Формула Эйнштейна не учитывает наличие у частиц поверхностных слоев (адсорбционного, сольватного, ДЭС).
уд 2,5 1 k , где k |
б |
|
б – объемная доля слоев.
Для описания вязкости разбавленных растворов полимеров используется уравнение Штаудингера: уд kMc ,
где k – константа, характерная для данного полимера в данном растворителе;
M – молярная масса полимера;
c – массовая концентрация полимера.
Приведенная вязкость: уд kM используется для определения
c
M полимеров.
Уравнение Штаудингера справедливо только для растворов полимеров с короткими и жесткими цепями (палочкообразные макромолекулы).
Уравнение Марка – Куна – Хаувинка (Гувинка)
kM ,
|
|
|
уд |
|
|
|
где lim |
|
|
|
|
, |
|
c 0 |
|
|
|
|||
|
|
с |
|
|||
|
|
|
|
|
|
|
k и – константы для полимера и растворителя; |
||||||
– характеристическая вязкость. α отражает формулу и плотность клубка макромолекулы, значения от 0,5 до 1. В плохом растворителе (клубок свертывается) значение 0,5 . 1 в хорошем растворителе, макромолекула "расправляется" и занимает большой объем.
81
