
Kolloidnaya_khimia_2
.pdf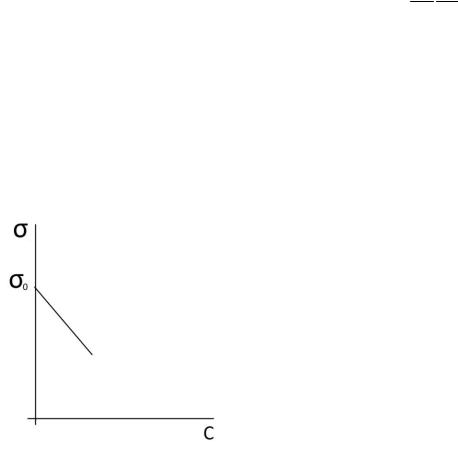
ЛЕКЦИЯ 4
4.1. Адсорбция ПАВ и полимеров
Как отмечалось, ПАВ, имеющие дифильное строение, отличаются высокой поверхностной активностью по отношению к воде. Их концентрация в поверхностном слое на 4…5 порядков выше, чем в объеме. Отмеченная особенность позволяет пренебречь различием между величинами A и , то есть для истинных ПАВ можно принять, что A . Из этого следует, что для растворов ПАВ все уравнения адсорбции, включающие А будут справедливы. если в них заменить A на .
Закон Генри в этом случае имеет вид (для неионогенных ПАВ):
A Kc
Сопоставим его с уравнением Гиббса c d
RT dc
cK |
c |
|
d |
; |
d KRTdc |
||||
RT |
|
dc |
|||||||
|
|
|
|
|
|
|
|
||
|
0 |
d c KRTdc ; |
0 |
KRTc |
|||||
|
|
|
0 |
|
|
|
|||
Зависимость f (c) линейна в области действия закона Генри.
Зависимость поверхностного натяжения от концентрациив области действия закона Генри (рис.11).
d |
|
||
g |
|
|
KRT , то есть для ПАВ по- |
|
|||
dc c 0 |
|
||
верхностная активность пропорциональна константе Генри.
С ростом концентрации ПАВ воспользуемся уравнением Ленгмюра:
|
|
A A |
|
Kc |
|
|
|
c d |
|||||||
|
|
|
Kc |
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
RT dc |
||||||
|
|
d A RT |
|
|
Kdc |
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
1 Kc |
|||||||||||||
Рис.11 |
|
|
|
d c A |
|
|
RT |
|
Kdc |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
0 |
|
1 Kc |
|||||||
|
|
|
|
|
|||||||||||
0 |
A RT ln(1 Kc) или |
|
|
|
|
|
|
|
|
|
|
||||
|
0 A RT ln(1 Kc) |
|
|
|
|
|
|
|
|
|
|
||||
Данное уравнение является аналогом эмпирического уравнения Шишковского, имеющего следующий вид:
23
0 0b ln(1 ac )
|
Из сопоставления: A |
|
b 0 |
; |
1 |
K . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
RT |
|
a |
|
|
|
|
|
|
|
Величина ( b ) характеризует размер молекулы в адсорбционном |
||||||||||||||||||
слое; |
1 |
|
|
|
характеризует поверхностную активность |
и |
называется |
||||||||||||
|
|
|
|
|
|||||||||||||||
|
a |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
удельной капиллярной постоянной. |
|
|
|
|
|
||||||||||||||
|
Рассмотрим построение изотермы поверхностного натяжения с |
||||||||||||||||||
помощью уравнения Шишковского. |
|
|
|
|
|
||||||||||||||
|
При |
|
достаточно высоких |
концентрациях |
ПАВ |
|
c |
1, тогда |
|||||||||||
|
|
|
a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b ln( |
c |
) . |
|
|
|
|
|
|
|
|
|
|
|||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||
tan 0b |
или tan 0b . |
Зависимость ln c |
линейна |
в |
области |
||||||||||||||
средних значений концентрации. Изветсно, что |
tan A RT , |
отсюда |
|||||||||||||||||
можно найти A , а следовательно S0 и .
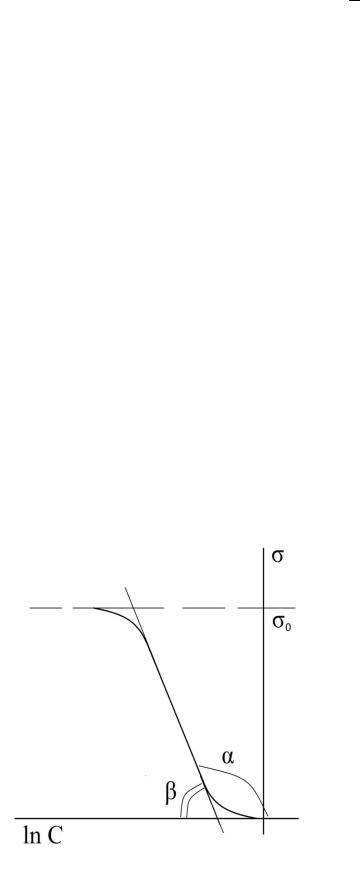
Зависимость ln c в области средних значений концентрации
(рис.12).
Приведенный способ определения характеристик поверхностного слоя выгодно отличается от способа графического дифференцирования (проведение касательных), поскольку обеспечивает большую
точность. |
|
|
|
|
|
|
Адсорбция |
полимеров |
|||
|
существенно |
отличается |
от |
||
|
адсорбции низкомолекуляр- |
||||
|
ных соединений, в том числе и |
||||
|
ПАВ. Специфика обусловлена |
||||
|
разнообразием |
конформаций, |
|||
|
которые |
может |
принимать |
||
|
гибкая |
макромолекула поли- |
|||
|
мера в объеме раствора и на |
||||
|
межфазной поверхности. По- |
||||
|
этому строгое |
теоретическое |
|||
|
рассмотрение |
адсорбции |
по- |
||
|
лимеров возможно только на |
||||
|
основе |
статистических мето- |
|||
Рис.12 |
дов. |
|
|
|
|
Макромолекулы линейных и разветвленных полимеров располагаются на плоской поверхности таким образом, что контактирует с
24
ней только часть молекулярных сегментов, другая часть, оставаясь в объеме, образует петли и хвосты.
Анализ состояния макромолекул в поверхностном слое проводят на основании уравнения Перкеля
A K M , lg A lg K lg M ,
где A – емкость монослоя в отношении полимера,
M– средняя молекулярная масса полимера,
– параметр, зависящий от конформации макромолекул.
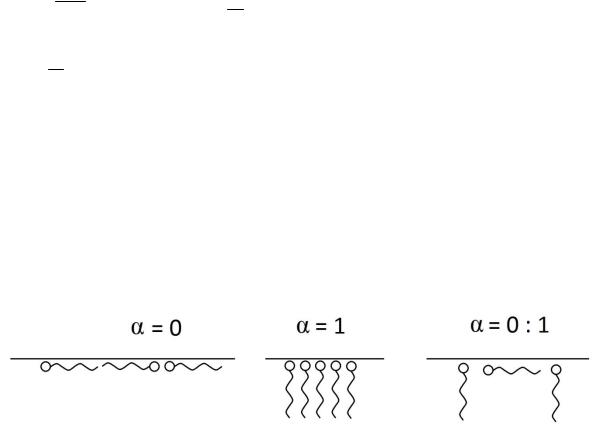
При 0 имеет место плоская ориентация адсорбированных молекул.
При 1 адсорбированные молекулы располагаются вертикально, закрепляясь на поверхности одним концом. В интервале от 0 до 1 возможны различные конформации на поверхности – в виде деформированных клубков или петель и хвостов разной длины, погруженных в раствор (рис.13).
Рис.13
ЛЕКЦИЯ 5
5.1.Адгезия, смачивание и растекание жидкостей
Вгетерогенных системах рассматривают межмолекулярные взаимодействия внутри фаз и между фазами.
Притяжение атомов и молекул внутри отдельной фазы называется когезией. Она определяет существование веществ в конденсированном состоянии. Когезию характеризуют такие параметры как
энергия кристаллической решетки, Tкип, летучесть, энергия парообразования и др.
Работа когезии – это затрата энергии на обратимый разрыв тела по сечению, равному единицы площади
WK 2
25
Понятие адгезии, смачивания и растекания относятся к межфазным взаимодействиям, наблюдаемым между конденсированными фазами. Адгезия (прилипание) – это межфазное взаимодействие тел разной природы. Она обеспечивает между двумя телами (объектами) соединение определенной прочности, обусловленное межмолекулярными силами.
Явление адгезии и смачивания широко распространены как в природе, так и в различных областях человеческой деятельности. Склеивание материалов, пропитка материалов, нанесение лакокрасочных и неорганических покрытий, получение материалов на основе связующих и наполнителей (бетон, резина, стеклопластики, ДСП и др.), сварка и пайка металлов, печатание, крашение тканей – все эти процессы связаны с адгезией и смачиванием.
Адгезия есть результат стремления системы к самопроизвольному уменьшению поверхностной энергии. Найдем соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов.
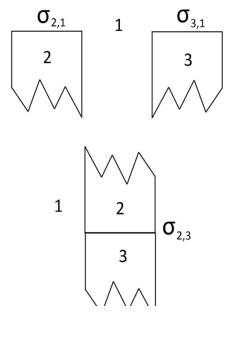
Представим две конденсированные фазы 2, 3 (жидкость и твердое тело), имеющие поверхности на границе с воздухом 1 (рис.14).
При совмещении этих поверхностей, то есть при нанесении одного вещества на другое, происходит адгезия. В результате начальная энергия Гиббса системы уменьшается на величину, равную
работе адгезии W A , т.е. W A G .
GН 2,1 3,1, GК 2,3 , G GК GН 2,3 2,1 3,1,
где GН – энергия Гиббса натяжения; GК – энергия Гиббса когезии;
2,1 – поверхностное натяжение на границе 2,1;
3,1 – поверхностное натяжение на границе 3,1;
2,3 – поверхностное натяжение на границе 3,2. W A 2,1 3,1 2,3 Уравнение Дюпре.
26
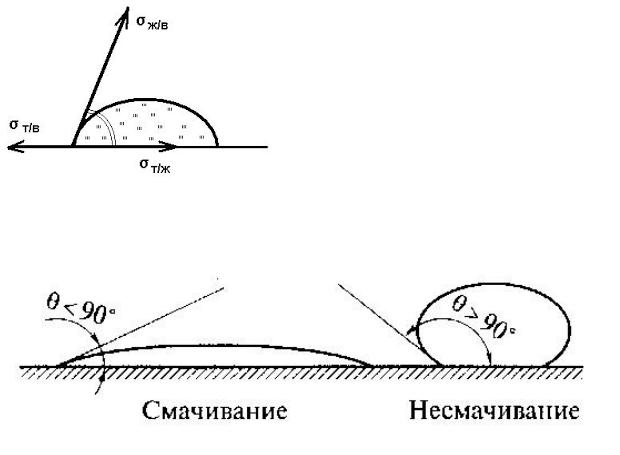
Чем больше работа адгезии, т.е. межфазное взаимодействие, тем меньше межфазное натяжение. При 2,3 0 происходит взаимное рас-
творение фаз 2,3.
Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или жидким телом при наличии одновременного контакта трех несмачивающихся фаз, одна из которых обычно газ (воздух) (рис. 15). Степень смачивания количественно характеризуется краевым углом смачивания .
Если капля жидкости не растекается, то в состоянии равновесия справедливо:
|
|
|
|
|
|
cos или cos |
3,1 2,3 |
– закон Юнга. |
|
3,1 |
2,3 |
2,1 |
2,1 |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Чем меньше , тем лучше смачивается поверхность (рис. 16):
Смачиваемость водой некоторых тел характеризуется следующими: кварц, стекло – 0º; малахит – 17º; графит – 55º; тальк – 69º; парафин – 106º; фторопласт – 108º (хуже всех).
Рис.15 Угол смачивания очень чувствителен к загрязнениям, поэтому
его часто используют для определения чистоты поверхности.
Рис.16
Уравнение Дюпре самостоятельно почти не используется из-за трудности определения 3,1 и 2,3 , но в сочетании с законом Юнга
можно получить практически важное соотношение.
W A 2,1 3,1 2,3 ; 3,1 2,3 2,1 cos
27

W |
|
|
|
|
|
cos |
|
(1 cos) или |
W A |
1 cos |
A |
2,1 |
2,1 |
2,1 |
|
||||||
|
|
|
|
2,1 |
|
|||||
|
|
|
|
|
|
|
|
|
||
W A 1 cos – уравнение Дюпре – Юнга, позволяющее рассмат-
2,1
ривать работу адгезии.
W A |
|
1 cos |
, где W |
|
2 |
|
. |
|
|
K |
2,1 |
||||
WK |
2 |
|
|
|
|||
|
|
|
|
|
|||
Здесь четко просматривается различие между адгезией и смачиванием. Последнее имеет место только при наличии трех сопряженных фаз.
При 0 , W A WK ; при 90 , W A 12 WK смачивающей жид-
кости.
Из уравнения Дюпре – Юнга следует, что для увеличения смачивания надо увеличить W A или уменьшить поверхностное натяжение
смачивающей жидкости (введением ПАВ, повышением T ), что используется например при стирке тканей.
Рассмотрим явление растекания жидкости (2) по поверхности
(3). При растекании уменьшается поверхность на границе 1-3 и увеличивается на границах 2-1 и 2-3. Изменение энергии Гиббса при этом:
|
|
dG 2,3dS 2,1dS 3,1dS или |
|
|
||
|
|
dG ( 2,3 |
2,1 3,1)dS |
|
|
|
Для |
самопроизвольного |
процесса |
dG 0 |
и |
dS 0 , |
|
2,3 2,1 3,1 0 |
или 2,3 2,1 3,1, то есть уменьшение межфазно- |
|||||
го натяжения 2,3 |
(увеличение работы адгезии) |
и 2,1 |
способствует |
|||
растеканию жидкости на поверхности смачиваемого тела. Из уравнения Дюпре 3,1 2,3 W A 2,1 следовательно условие растекания
W A 2,1 2,1 или W A 2 2,1 ; W A WK .
Т.о., растекание происходит в том случае, если работа адгезии превышает работу когезии растекающейся жидкости. Жидкость растекается, если ее межмолекулярные связи разрушаются в результате адгезии.
Коэффициент растекания Гаркинса:
или f W A WK .
28

Жидкость растекается по поверхности, если f 0 и не растекается, если f 0 .
Например, на поверхности воды при 20ºС для олеиновой кисло-
ты f 24,6 |
мДж |
, для бензола |
f 8,8 |
мДж |
, для сероуглерода |
f 8,7 |
мДж |
|
м 2 |
м 2 |
м 2 |
||||||
|
|
|
|
|
,для метилиодида f 26,5 мДж .
м2
Явление адгезии, смачивания и растекания всегда сопровождаются выделением теплоты, которая называется теплотой смачивания, хотя правильнее ее было бы назвать теплотой адгезии.
5.2. Капилярные явления
Сначала рассмотрим влияние дисперсности на состояние жидкостей. Вследствие избыточной поверхностной энергии жидкости, благодаря своей подвижности, приобретают наиболее экономическую сферическую форму в условиях невесомости. В морях и океанах вода имеет плоскую поверхность поскольку на нее действует сила тяжести. С уменьшением количества жидкости роль силы тяжести снижается, увеличивается удельная поверхность. С ростом поверхностной энергии появляется кривизна поверхности жидкости, например, капельки тумана имеют сферическую форму. С появлением кривизны поверхности в фазе возникает дополнительное давление P , направленное к
центру кривизны, и определяемое по уравнению Лапласа: P |
dS уд |
, |
|||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
где |
dS уд |
– кривизна поверхности. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для сферы: S |
|
4 r 2 , dS |
|
|
8 rdr ; |
|
V |
4 |
r 3 , |
dV 4 r 2dr , тогда |
||||||||||
|
уд |
уд |
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кривизна поверхности будет равна: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
dS уд |
|
|
8 rdr |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
dV |
|
4 r |
dr |
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
В этом случае |
P |
2 |
или |
P 4 D , то есть чем выше дисперс- |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ность, тем больше внутреннее дополнительное давление, появляющееся в частице жидкости. Фактически происходит самопроизвольное понижение свободной поверхностной энергии dS уд за счет со-
29
вершения работы по уменьшению объема частиц жидкой фазы, т.е. переход этой энергии в энергию механическую: dS уд PdV .
Все вышеизложенное позволяет объяснить причину возникновения капиллярных явлений.
Капилярными явлениями называются процессы самопроизвольного движения жидкостей внутри узких протяженных сосудов (капилляров). Расстояние между стенками сосудов должно быть соизмеримо с радиусом кривизны поверхности жидкости (в ведре с водой мениска нет, а в бюретке уже есть). Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярах определяется величи-
ной краевого угла смачивания . |
|
|
|
|
|
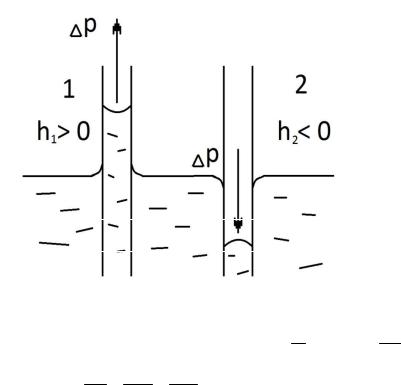
Рассмотрим модель двух капилляров (рис.17). |
|
||
|
|
|
Стенки капилляра 1 |
|
|
|
гидрофильны, а капиляра 2 |
||
|
|
– гидрофобны (1 – стекло, |
||
|
|
2 – тефлон). С появлением |
||
|
|
кривизны поверхности ра- |
||
|
|
диуса r в жидкости возни- |
||
|
|
кает |
дополнительное |
дав- |
|
|
ление P , направленное к |
||
|
|
центру кривизны, благода- |
||
|
|
ря чему в 1 случае жид- |
||
|
Рис.17 |
|||
|
кость |
растягивается, |
||
|
|
|||
|
|
а во 2 – снижается. |
|
|
|
|
|
Сжимающая |
(или |
|
|
растягивающая) |
сила |
|
P FS или P mgS . P mgS mghSh mghV gh , P gh( 0 ) ,
где и 0 – соответственно плотности жидкости и газа (возду-
ха);
g– ускорение свободного падения;
h– высота опускания или поднятия капиляра.
Согласно уравнению Лапласа |
P |
2 |
, тогда в состоянии равно- |
|
r |
||||
|
|
|
||
весия: |
|
|
|
30
|
2 |
gh( |
|
) |
или h |
2 |
– высота капиллярного подня- |
|
0 |
rg( 0 ) |
|||||
|
r |
|
|
|
|||
|
|
|
|
|
|||
тия (опускания)
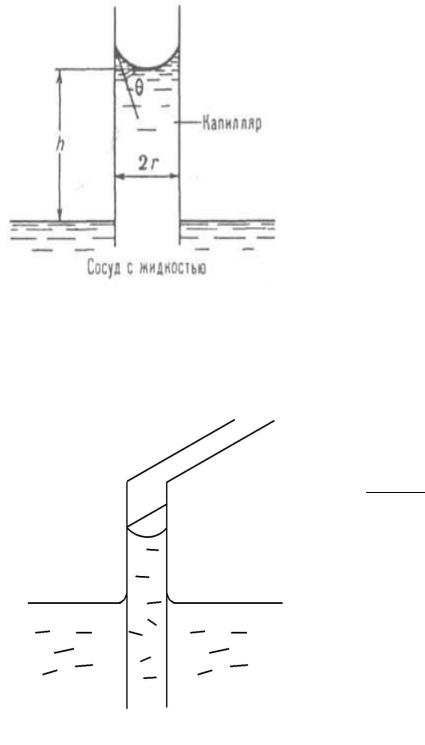
Радиус кривизны поверхности ( r ) трудноопределим, поэтому его лучше связать с радиусом капилляра ( r0 ) который можно легко измерить.
Из рис. 18 видно, что r0 r cos , то- |
||||
гда h |
2 cos |
|
– формула Журе- |
|
r g( |
|
) |
||
0 |
0 |
|
|
|
на. |
|
|
|
|
Капилярным втягиванием жид- |
||||
костей объясняются процессы про- |
||||
питки бумаги, картона, тканей, ДСП |
||||
и др. Подъем |
воды из почвы по |
|||
Рис.18 |
стволам растений происходит благо- |
|
даря волокнистому (капиллярному) |
||
|
строению древисины. Процессы кровообращения в кровеносных сосудах тоже являют собой пример капиллярных явлений.
Для двух пластин, погруженных в жидкость и имеющих между собой зазор d (рис 19), формула Журена имеет вид:
h 2 cos . dg
Если же пластинки прижать друг к другу так, чтобы между ними оставалась прослойка смачивающей их жидкости, то они будут испытывать сжимающее давление. Сила притяжения между пластинами, смоченными жидкостью определяется уравнением:
Рис.19 |
2 cos |
, |
|
F |
|||
d |
|||
|
|
где S – поверхность соприкосновения пластин.
Следует подчеркнуть, что капиллярные явления проявляются на границе трех фаз: тв – ж – газ. Капилярными явлениями объясняется
31

комкование порошков при сушке; формуемость влажного песка; влажность соли и сахара.
Капилярные явления имеют место на границе трех фаз. Они широко используются в порометрии (измерение объема пор пористых тел).
Пористые тела (к ним относятся и активированные угли) делятся на три группы: макропористые с радиусом пор свыше 100...200 нм
и S |
|
|
0,5...2 |
м |
2 |
; переходнопористые с радиусом пор от 2 до 100 нм и |
||||||
уд |
|
|
|
|
||||||||
г |
||||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
м2 |
|
|
|||||
S |
уд |
10...500 |
|
|
|
|
; микропористые с радиусом пор от 0,5 до 2 нм и |
|||||
|
г |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
S |
|
500...1000 |
|
м |
2 |
. |
||||||
уд |
|
|
|
|
||||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
г |
||||
Одной из основных характеристик пористой структуры тела является пористость, то есть отношение объема пор к общему объему
тела: П VП – доля пустот в структуре тела.
Vобщ
Отличают поры и капилляры открытые, тупиковые и закрытые. Общая пористость тела: П ПО ПТ ПЗ , где ПО,Т , З – объем соответ-
ствующих пор в единице объема пористого тела.
ЛЕКЦИЯ 6
6.1. Электроповерхностные явления
Стремление гетерогенной системы к уменьшению поверхностной энергии взывает самопроизвольный процесс определенного ориентирования полярных молекул, ионов и электронов в поверхностном слое, вследствие чего соприкасающиеся фазы приобретают заряды противоположного знака, но равной величины. В результате на границе раздела фаз возникает двойной электрический слой (ДЭС), являющийся аналогом электрического конденсатора, но особенностями которого является то, что обкладки такого конденсатора принадлежат разным фазам, находящимся не в одинаковых агрегатных состояниях.
Различают три возможных варианта механизма образования
ДЭС.
1. ДЭС образуется в результате перехода ионов или электронов из одной фазы в другую (поверхностная ионизация, термоэлектронная эмиссия). Например, с поверхности металла в газовую фазу переходят
32
