2.2. Обработка результатов однократных измерений

Оценку погрешности результата измерения выполняют при разработке методик выполнения измерений (МВИ). Источниками погрешностей являются модель объекта измерений, метод измерения, средства измерений, оператор, влияющие факторы условий измерений, алгоритм обработки результатов наблюдений. Как правило, погрешность результата измерения оценивается при доверительной вероятности P = 0,95.

При выборе значения P необходимо учитывать степень важности (ответственности) результата измерений. Например, если ошибка в измерении может привести к гибели людей или к тяжелым экологическим последствиям, значение P должно быть увеличено.

Измерения с однократными наблюдениями

За результат измерения в этом случае принимается результат однократного наблюдения x (с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.

Доверительные границы НСП результата измерения Θ(P) вычисляются по формуле:

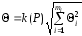(2.7)

где k(P) – коэффициент, определяемый принятой P и числом m_i составляющих НСП; Θ(P) – найденные нестатическими методами границы i-й составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале).

При P = 0,95 и 1,1 соответственно при любом числе слагаемых m_i. При P = 0,99 значения k(P) следующие:

mi	5 и более	4	3	2
k(P)	1,45	1,40	1,30	1,20

Если составляющие НСП распределены равномерно и заданы доверительными границами Θ(P), то доверительную границу НСП результата измерения вычисляют по формуле:

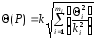, (2.8)

где k и k_i – те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности P и P_i соответственно; m_i – число составляющих НСП.

Среднее квадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов:

1. Если технической документации на СИ или МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т. д.), то СКО вычисляют по формуле:

S(x) =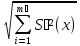, (2.9)

где 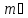– число составляющих случайной погрешности;S_i – значения СКО этих составляющих.

Доверительную границу случайной погрешности результата измерения ε(P) в этом случае вычисляют по формуле:

ε(P) = z_P/2S(x), (2.10)

где z_P/2 – значение нормированной функции Лапласа в точке P/2 доверительной вероятности P:

P	0,90	0,95	0,96	0,97	0,98	0,99
zP/2	1,65	1,96	2,06	2,17	2,33	2,58

Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами ε_i(P) при одной и той же доверительной вероятности P, то доверительную границу случайной погрешности результата измерения с однократными наблюдением при доверительной вероятности вычисляют по формуле:

ε(P) =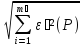. (2.11)

Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений n_i < 30, то:

ε(P) =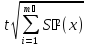, (2.12)

где t – коэффициент Стьюдента, соответствующий наименьшему числу наблюдений n_min из всех n_i, можно найти в любом справочнике по теории вероятностей; S(x) – оценка СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (2.18).

Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (2.12) m₂=1.

Если случайные составляющие погрешности результата наблюдений представлены доверительными границами ε(P_i), соответствующими разными вероятностями P_i, то сначала определяют СКО результата измерения с однократными наблюдением по формуле:

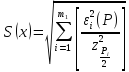, (2.13)

где 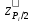– значение функции Лапласа.

Затем вычисляют ε(P) по формуле (2.12).

Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ:

если

Θ(P)/S(x) < 0,8, (2.14)

то НСП Θ(P) пренебрегают и окончательно принимают ε(P) за погрешность результата измерения ∆(P) при доверительной вероятности P;

если

Θ(P)/S(x) > 0,8, (2.15)

то пренебрегают случайной погрешностью и принимают ∆(P)=Θ(P);

если 0,8 ≤ Θ(P)/S(x) ≤ 8, то доверительную границу погрешности результата измерений вычисляют по формуле:

∆(P)=K_∑(γ)[ Θ(P)+ ε(P)]. (2.16)