
Лекции эконометрика 1-8 / Лекция 5
.pdf
Эконометрика 1 осень 2015
Лекция 5
30.09.2015

Гомоскедастичность ошибки
Случайная ошибка называется гомоскедастичной, если условная дисперсия относительно постоянна
для = 1, 2, … (т.е. var |
|
|
= |
= , = 1, … , ). В |
|
|
|
|
частности, условная дисперсия относительно не зависит от .
В противном случае ошибка называется гетероскедастичной.
2

Графическая иллюстрация
3

Следствия гомоскедастичности
МНК оценки коэффициентов – несмещенные, состоятельные и асимптотически нормальные как для в случае гомоскедастичности, так и в случае гетероскедастичности ошибок
НО! Они эффективны только в случае гомоскедастичности ошибок
4

Гомоскедастичность: оценка дисперсии оценок коэффициентов
Для случая гомоскедастичных ошибок формулы оценок
дисперсии имеют вид:
2 =
1
и
2 =
0
где 2 |
= |
1 |
|
2 |
= |
|
|
|
|
||||||
|
|
−2 |
=1 |
|
|
−2 |
|
|
|
|
|
|
|||
2
− 2 , =1
1 |
|
|
2 |
|
2 |
|
|
|
=1 |
|
|
|
|||
|
|
, |
|||||
|
|
− 2 |
|||||
=1 |
|
|
|
|
|
|
|
5

Как бороться с гетероскедастичностью ошибок?
-Моделировать (ВМНК)
-Устойчивые к гетероскедастичности стандартные ошибки Эйкера-Хьюбера-Уайта (состоятельные при выполнении трех предположений МНК):
|
|
|
1 |
|
|
1 |
|
|
− |
2 |
2 |
|||||||
2 |
|
= |
× −2 |
, |
||||||||||||||
|
=1 |
|
|
|
|
|
|
2 |
||||||||||
1 |
|
|
|
1 |
|
|
− 2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
||||
|
2 |
|
|
− 2 |
|
|
|
|
|
|||||||||
|
= |
× |
=1 |
|
|
|
|
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
0 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
||
|
где = 1 − |
1 |
|
2 |
|
6 |
|
|
=1 |
|
|
|
|
|
|
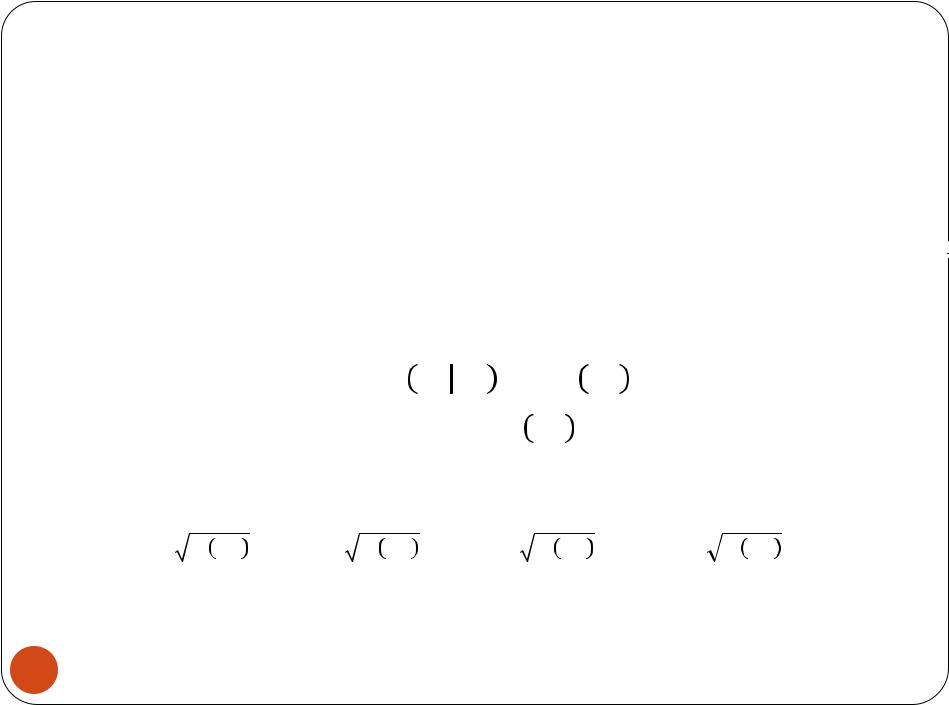
Взвешенный метод наименьших квадратов (ВМНК)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
0 |
+ |
1 |
+ |
|
(1) |
|
|
|
|
|
|
Пусть
var = ,
где – некоторая константа, - известная функция. Рассмотрим преобразованные переменные:
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
; = |
|
|
; = |
|
|
; и |
|
= |
|
. |
(2) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
7

Взвешенный метод наименьших квадратов (ВМНК)
Тогда (1) примет вид
= |
|
+ |
1 |
|
+ |
. |
(3) |
|
0 0 |
|
1 |
|
|
|
И
1 - ВМНК-оценка коэффициента наклона в уравнении (1) и она BLUE
8
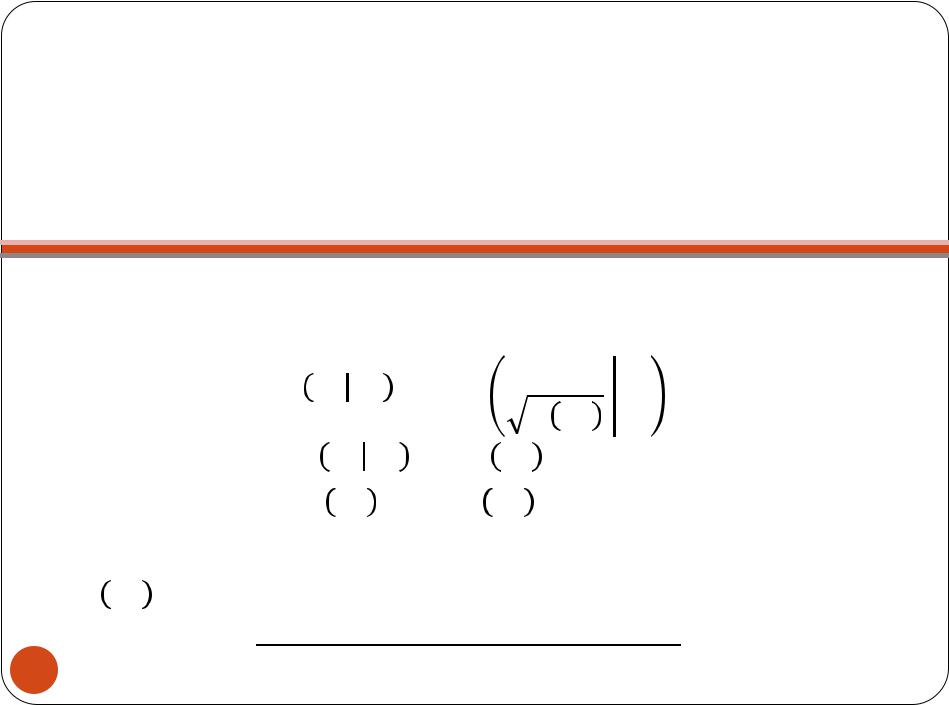
Взвешенный метод наименьших квадратов (ВМНК)
Заметим, что
var |
|
|
= var |
|
|
= |
|||||
|
|
|
|
||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
var |
|
|
|
|
|
|
|
|
||
= |
|
|
|
|
= |
|
|
|
= λ = const |
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
НО!
- в реальной жизни неизвестна → такая оценка называется недоступной ВМНКоценкой
9

Доступный ВМНК - алгоритм
1.Оцените регрессию (1) на при помощи МНК и вычислите остатки
, i=1,..., n.
2.Оцените предполагаемую модель функции условной дисперсии
var (оцениваем 2 на набор переменных, от которых она зависит).
3.Используйте оцененную функцию для расчета предсказанных значений функции условной дисперсии var .
4.Умножьте зависимую переменную и регрессоры (в том числе и свободный член) на величину, обратную квадратному корню из оцененной функции условной дисперсии (см. (2)).
5.Оцените коэффициенты взвешенной регрессии (3) при помощи МНК; полученные оценки являются ВМНК–оценками (1).
10
