
P4_11_2012
.pdf
2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
Пример 3. На лѐгкой пружине жѐсткостью k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
подвешен груз массой m . Показать, что верти- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
кальные собственные колебания такого пружин- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ного маятника гармонические, и найти их период. |
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
ненапряженная |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Направим ось x вниз (рис. 14), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пружина |
||
|
|
|
|
|
0 |
|
|
|
|
равновесияположение |
|||||||
F |
|
|
|
|
|
|
|||||||||||
начало координат поместим в точку, соответ- |
|
|
|
|
|
|
|||||||||||
ствующую равновесному положению груза. В |
|
|
|
|
|
|
x(t) |
текущая коор- |
|||||||||
этом положении пружина растянута по сравне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дината груза |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
нию с ненапряжѐнным состоянием на величину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x0 , причѐм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
mg |
|
|
|
|
|
|
|
|
|
x |
||||
kx0 mg. |
(21) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1-й способ. Используется второй закон Нью- |
|
|
|
|
|
|
Рис. 14 |
||||||||||
тона. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если текущая координата x x(t) , то проекция на ось x силы F , действую-
щей на груз со стороны пружины, |
|
Fx k(x0 x). |
(22) |
Равенство (22) справедливо для любого значения координаты x колеблющегося груза, что, вообще говоря, нужно проверить, т. к. мы хотим получить дифференциальное уравнение колебаний, справедливое не только для одного значения x , а для всех значений.
Запишем уравнение движения груза (уравнение второго закона Ньютона) в проекциях на ось x , учитывая, что проекция на ось x ускорения груза есть вто-
рая производная x '' от координаты по времени: |
|
mx '' Fx mg. |
(23) |
С учѐтом (22) и (21) уравнение (23) принимает вид: |
|
x '' |
k |
x 0. |
(24) |
|
m |
||||
|
|
|
Видно, что это дифференциальное уравнение гармонических колебаний, пери-
од которых |
|
|
|
|
|
|
|
|
|
|
|
T 2 |
m |
. |
(25) |
||
|
|||||
|
|
k |
|
||
2-й способ решения. Используется закон сохранения энергии.
За нулевой уровень потенциальной энергии груза в поле тяжести удобно взять положение равновесия. Полная механическая энергия колебаний системы пред-
ставляет собой сумму кинетической энергии груза 12 m(x ')2 , потенциальной энергии груза в поле тяжести mg( x) mgx и потенциальной энергии деформа-
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
21

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
ции пружины 12 k(x0 x)2 . Здесь x ' проекция скорости груза на ось x , еѐ
квадрат равен, естественно, квадрату модуля скорости.
Полная механическая энергия при колебаниях должна сохраняться:
m(x ')2 |
k(x x)2 |
|
|
||
|
|
0 |
mgx const. |
(26) |
|
2 |
2 |
||||
|
|
|
|||
Дифференцируем (26) по времени:
mx ' x '' k(x0 x)x ' mgx ' 0.
С учѐтом (21) после простых преобразований получаем x '' mk x 0 , что
совпадает с (24). Итак, колебания гармонические с периодом, даваемым (25).
3-й способ. Сведение задачи к известной другой.
Заметим, что сила тяжести mg есть постоянно действующая на груз сила,
аналогичная силе F0 в примере 2. Поэтому сразу можно сказать, что колебания подвешенного на пружине груза будут гармоническими с периодом
|
|
|
|
T 2 |
m |
. |
(27) |
|
|||
|
k |
|
|
Причѐм новое положение равновесия висящего груза сместится на величину x0 вниз ( kx0 mg ) по отношению к положению равновесия при отсутствии
поля тяжести. Около нового положения равновесия и колеблется подвешенный yгруз.
Теперь становится ясным, почему говорят, что период колебаний пружинного маятника определяется формулой (27), и не указывают при этом, скользит ли груз по столу или подвешен на пружине. Это полезно знать.
Пример 4. Показать, что в однородном поле тяжести малые собственные колебания в вертикальной плоскости математического маятника длиной l являются гармоническими и найти их период.
|
|||||||
|
Решение. Пусть у |
маятника длина нити l и масса шарика m . За колеблющу- |
|||||
|
|
|
|
|
|
|
юся физическую величину удобно взять угол от- |
|
|
|
|
|
|
|
клонения нити от вертикали (рис. 15). Будем считать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положительным, если маятник отклонѐн вправо от |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
положения равновесия, и отрицательным, если он от- |
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
клонѐн влево. |
||
|
|
|
|||||
|
|
|
|||||
|
|
|
m. |
|
|
|
Выразим кинетическую и потенциальную энергии |
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
шарика массой m в произвольный момент времени t |
|
П= 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
через угол (t) и производную угла по времени |
|
|
Рис. 15 |
' '(t). Угловая скорость шарика ', его линейная |
||||
|
|
|
|
|
|
|
скорость v 'l и кинетическая энергия |
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
22

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
K 12 mv2 12 ml2 ( ')2 .
Если за нулевой уровень потенциальной энергии ( П 0 ) взять уровень, соответствующий нахождению шарика в положении равновесия маятника, то потенциальная энергия шарика в момент отклонения нити на угол окажется
П mg(l l cos ) . Поскольку 1 cos 2sin2 2 , то П 2mgl sin2 2 . Для малых углов можно считать, что значения их синусов приблизительно равны самим углам (в радианах). Поэтому sin 2 2 , и можно принять, что
|
2 |
|
1 |
|
2 |
|
|
П 2mgl |
|
|
|
|
mgl |
|
. |
|
|
|
|||||
|
2 |
|
|
2 |
|
|
|
Полная энергия системы, равная K П при колебаниях сохраняется. Следовательно, 12 ml2 ( ')2 12 mgl 2 const .
Продифференцируем последнее равенство по времени:
12 ml2 2 ' '' 12 mgl2 ' 0.
После упрощения имеем: '' gl 0.
Нами получено дифференциальное уравнение гармонических колебаний вели-
|
|
|
чины с циклической частотой |
g |
. |
|
||
|
l |
|
Итак, малые колебания математического маятника являются гармоническими с
периодом T |
2 |
2 |
l |
. |
|
|
|||
|
|
g |
||
Пример 5. Дан колебательный контур без затухания (сопротивление равно нулю) с постоянными ѐмкостью C и индуктивностью L . Показать, что свободные
электрические колебания в контуре гармонические и |
|
|
|
|
|
|
|
|
найти их период. |
|
|
|
|
|
K |
|
|
Решение. Если зарядить конденсатор и затем за- |
1 |
|
|
C |
|
|
||
|
|
|
|
|
|
|||
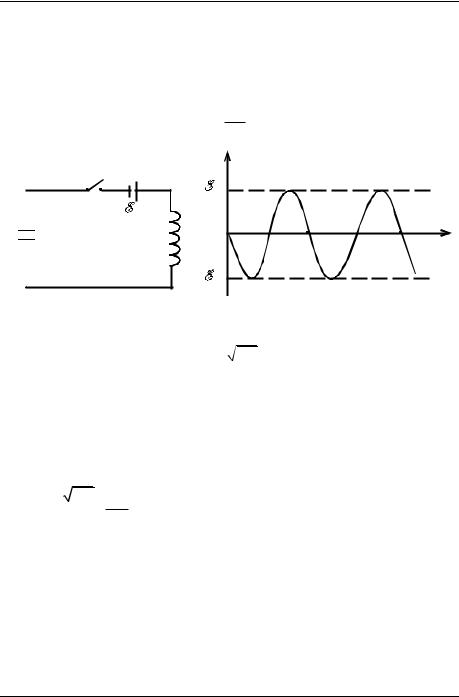
мкнуть ключ, то в схеме на рис. 16 возникнут колеба- |
|
|
|
|
L |
|||
2 |
|
|
q |
|
|
|||
ния заряда на конденсаторе, колебания тока в цепи, |
|
|
|
|
|
|
||
|
|
|
|
обход |
|
|||
колебания ЭДС самоиндукции в катушке и т. д. За |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
колеблющуюся величину удобно взять заряд на одной |
|
|
|
|
|
|
|
|
из обкладок конденсатора. |
|
|
|
|
Рис. 16 |
|||
1-й способ решения. Используем закон Ома. |
|
|
|
|
|
|
|
|
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
23

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
Выберем положительное направление обхода контура, например по часовой
стрелке, как показано на рис. 16. Это означает, что ток I положителен, если его направление совпадает с положительным направлением обхода, и отрицателен, если не совпадает. Аналогичное можно сказать и про знак ЭДС самоиндукции E , при расчѐте которой по формуле E LI ' автоматически будет получаться знак у ЭДС, согласованный с направлением обхода.
Обозначим через q заряд той обкладки конденсатора, для которой q' I (для другой обкладки q ' I , что не очень удобно). Это легко сделать, если учесть,
что q' q |
при t 0 . Для схемы на рис. 16 q следует взять на нижней об- |
||||||
t |
|
|
|
|
|
|
|
кладке. |
|
|
|
|
|
|
|
По закону Ома для участка 1 L 2 |
|
|
|
|
|
|
|
|
( 1 2 ) E IR. |
|
|
|
(28) |
||
Поскольку сопротивление в контуре R 0, |
|
|
|
|
q |
, |
|
2 |
|
||||||
|
|
1 |
|
|
C |
||
|
|
|
|
|
|
||
E LI ' L(q ')' Lq '' , то равенство (28) после деления на L принимает вид:
q '' |
1 |
q 0. |
(29) |
|
LC |
||||
|
|
|
Итак, получено дифференциальное уравнение гармонических колебаний вели-
|
|
1 |
|
|
|
|
|
чины q с циклической частотой ω |
|
|
и периодом T 2 LC. |
||||
|
|
|
|||||
|
|
|
|||||
LC |
|||||||
|
|
|
|
|
|
||
Полезно заметить, что при изменении заряда по гармоническому закону q q0 cos( t 0 ) ток
I q ' q0 sin( t 0 ) q0 cos( t 0 2 ),
ЭДС самоиндукции E LI ' Lq0 2 cos( t 0 ) и напряжение на конденсаторе U Cq qC0 cos( t 0 ) . Итак, заряд на конденсаторе, ток в катушке, ЭДС
самоиндукции в катушке и напряжение на конденсаторе совершают гармонические колебания с периодом T 2 
 LC , причѐм q,E , U колеблются в фазе, а
LC , причѐм q,E , U колеблются в фазе, а
колебания тока опережают колебания заряда по фазе на 2 .
2-й способ решения. Используется закон сохранения энергии.
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
24

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
Выберем положительное направление обхода контура и обозначим через q заряд той обкладки конденсатора, для которой q ' I . По закону сохранения
энергии |
|
|
|
|
|
|
|
|
|
|
|
|
|
LI 2 |
|
|
q2 |
const. |
(30) |
||||
|
2 |
|
2C |
||||||||
|
|
|
|
|
|
|
|||||
Продифференцируем (30) по времени: LII ' |
1 |
qq ' 0. Учитывая, что I q ' , |
|||||||||
C |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
а I ' (q ')' q '', получим |
q '' |
|
1 |
q 0 . Последнее уравнение совпало, что и |
|||||||
|
|
||||||||||
|
|
|
LC |
|
|
|
|||||
следовало ожидать, с уравнением (29), и дальнейшие рассуждения те же, что и в первом способе решения.
Пример 6. Батарею с постоянной ЭДС E0 подключили к катушке с индуктив-
ностью L и конденсатору с ѐмкостью C через ключ K . В начальный момент времени ключ K разомкнут и конденсатор заряжен до напряжения 3E0 (рис. 17).
Показать, что колебания тока в таком контуре гармонические и найти их период. Построить график зависимости тока от времени. Омическими сопротивлениями в схеме пренебречь.
Замечание. Если решение этого примера окажется непонятным, поскольку требуется значительная математическая культура, то рекомендуется прочитать и осмыслить только вывод в конце решения.
Решение. Выберем положительное направление обхода контура по часовой стрелке. Если через q обозначить заряд нижней обкладки конденсатора, то ток в
контуре I q' и ЭДС индукции в катушке E LI ' Lq '' . Заметим, что в состоянии равновесия колебательной системы (при отсутствии колебаний в контуре с замкнутым ключом) заряд нижней обкладки конденсатора равен CE0 . Ис-
пользуя закон Ома, получим: |
|
|
|
|
|
|
|
|
E |
|
E |
q |
0. |
|
|||
0 |
C |
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
После подстановки в последнее равенство выражения для E и простых пре- |
||||||||
образований имеем: |
|
|
|
|
|
|
|
|
q '' |
1 |
q |
|
E0 |
. |
(31) |
||
|
|
|
||||||
LC |
|
L |
||||||
|
|
|
|
|
|
|
||
Дифференциальное уравнение (31) отличается от уравнения (29) только тем, что в его правой части вместо нуля стоит постоянная величина E0  L. Уравнение
L. Уравнение
(31) можно привести к дифференциальному уравнению гармонических колебаний, аналогичному (17). Для этого запишем (31) в виде:
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
25
2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
q '' |
1 |
q CE0 0 |
(32) |
|
LC |
||||
|
|
|
и перейдѐм к новой переменной Q такой, что Q q CE0 . Ясно, что Q' q' и Q '' q '' , Поэтому (32) принимает вид:
_ 
+ 
|
|
Q '' |
1 |
Q 0. |
|
|
|
|
|
|
LC |
|
|
|
|
|
|
I |
|
|
+ |
2C 0 |
|
|
|
||
|
|
|
|
|
||
K |
|
|
|
|
|
|
|
0 |
|
|
|
T |
2T |
C |
|
|
0 |
|||
q |
|
L |
|
t |
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2C |
0 |
|
|
|
Рис. 17 |
|
|
|
|
Рис. 18 |
|
Получили дифференциальное уравнение гармонических колебаний для величины Q с циклической частотой 1/ 
 LC . Итак, Q Q0 cos( t ), где Q0 и некоторые постоянные. Отсюда следует, что ток изменяется по закону I Q0 sin( t ) . Значения Q0 и найдѐм, воспользовавшись тем, что при t 0 ток I 0 , а заряд конденсатора q 3CE0 , т. е. Q q CE0 2CE0 . Тогда получим Q0 2CE0 , 0 , и окончательно закон изменения тока имеет вид:
LC . Итак, Q Q0 cos( t ), где Q0 и некоторые постоянные. Отсюда следует, что ток изменяется по закону I Q0 sin( t ) . Значения Q0 и найдѐм, воспользовавшись тем, что при t 0 ток I 0 , а заряд конденсатора q 3CE0 , т. е. Q q CE0 2CE0 . Тогда получим Q0 2CE0 , 0 , и окончательно закон изменения тока имеет вид:
I 2CE0 sin t,
где 1/ 
 LC . Таким образом, колебания тока в контуре гармонические с периодом T 2
LC . Таким образом, колебания тока в контуре гармонические с периодом T 2 
 LC и амплитудой 2CE0 . График зависимости тока от време-
LC и амплитудой 2CE0 . График зависимости тока от време-
ни дан на рис. 18.
Вывод. При наличии в цепи колебательного контура батареи с постоянной ЭДС период колебаний тока в контуре остаѐтся таким же, как и в контуре без батареи. Кроме того, можно дополнительно показать, что колебания заряда конденсатора идут около нового равновесного значения заряда, равного CE0 , а коле-
бания напряжения на конденсаторе происходят тоже около нового равновесного значения напряжения, равного ЭДС батареи. Причѐм период колебаний заряда и напряжения будет таким же, как и при отсутствии батареи.
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
26

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
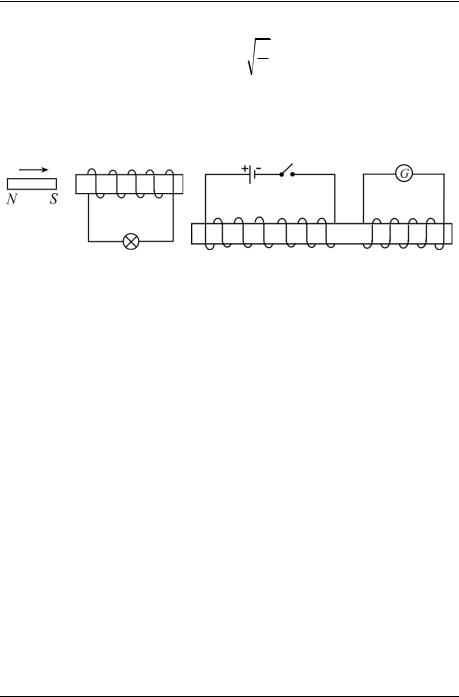
Пример 7. Последовательно с катушкой индуктивности L и конденсатором |
|||||||||||||||||
C через ключ K подключили батарею с по- |
|
|
|
|
+ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стоянной ЭДС E0 (рис. 19). В начальный мо- |
|
|
|
0 |
K |
|
|||||||||||
мент времени конденсатор не заряжен. Опре- |
|
|
C |
|
L |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||
делить максимальную величину тока в цепи |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
после замыкания ключа K. Омическим сопро- |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
тивлением в цепи пренебречь (МФТИ, 1982). |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
Решение. Можно было бы доказать, что ток |
|
|
|
|
Рис. 19 |
||||||||||||
в цепи изменяется по гармоническому закону |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
I =E0C sin t с циклической частотой |
|
1 |
|
. А далее заключить, что мак- |
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
LC |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
симальное значение тока I |
|
CE |
E |
|
C |
|
. Решая задачу, сформулированную |
||||||||||
0 |
0 |
|
|||||||||||||||
|
0 |
|
L |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в этом примере, таким способом, мы получим ответ на большее количество вопросов, чем спрашивается, и, в частности, докажем, что после замыкания ключа колебания тока гармонические и фактически найдѐм их период, что совершенно не требуется в задаче! Для ответа на некоторые вопросы в задачах с электрическими схемами иногда достаточно воспользоваться фундаментальными законами сохранения энергии и заряда, законом Ома, тем, что при максимальном значении изменяющегося тока его производная по времени равна нулю (вспомним исследование функций) и ЭДС самоиндукции тоже, соответственно, равна нулю, и другими соображениями.
Вернѐмся к нашей задаче. Пусть в момент, когда ток максимален и равен I0 , заряд на нижней обкладке конденсатора q . Такой же суммарный заряд пройдѐт с момента замыкания ключа и через источникE0 , и источник совершит работу qE0 .
По закону сохранения энергии работа источника пойдѐт на изменение энергии магнитного поля катушки индуктивности и электрического поля в конденсаторе:
|
|
|
|
LI02 |
|
|
|
q2 |
|
qE |
. |
(33) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
2C |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В любой момент для контура, используя закон Ома, можно записать |
|
|||||||||||||||
E |
|
E |
|
|
|
|
|
q |
IR. |
|
(34) |
|||||
0 |
инд |
C |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 и при максимальном значении тока |
||||||
Поскольку сопротивление контура R |
||||||||||||||||
I ЭДС индукции E инд 0 , то (34) принимает вид: |
|
|||||||||||||||
|
|
E |
|
|
|
q |
|
0. |
|
|
(35) |
|||||
|
|
0 |
|
С |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
27
2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
Исключая из (33) и (35) q, находим, что максимальное значение тока
I0 E0 
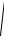 CL .
CL .
Контрольные вопросы
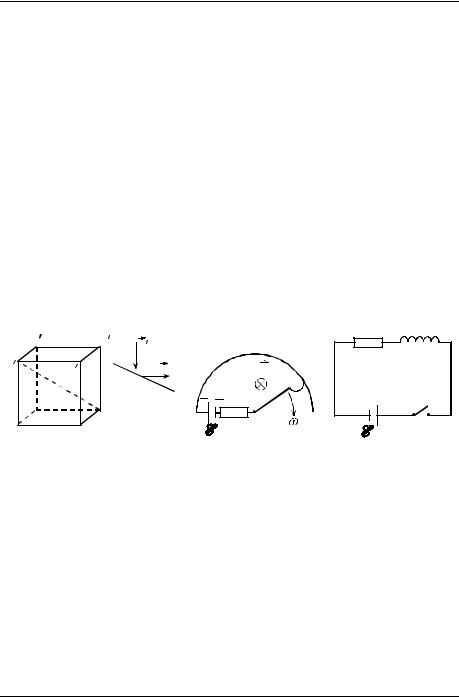
1. К катушке приближается постоянный магнит (рис. 20). В каком направлении течѐт ток через лампочку? Куда направлена сила, действующая на катушку со стороны магнита?
Рис. 20 |
Рис. 21 |
2.В кольцо вдвигается магнит. Какое электромагнитное явление наблюдается
вкольце из:
а) проводника; б) диэлектрика?
3.Две катушки намотаны на общий железный сердечник (рис. 21). В каком направлении потечѐт ток через гальванометр G после замыкания ключа?
4.Не выполняя тригонометрических преобразований, найти амплитуду A и циклическую частоту следующих гармонических колебаний:
1) |
|
|
, где t в секундах, |
x в сантиметрах. |
x 7 cos |
4t |
|||
|
8 |
|
|
|
2) |
I 12sin 20t 0,3 , где I в миллиамперах, t в секундах. |
|||
5. Груз колеблется вдоль оси x по закону x 8sin 4t 0,3 , где t в се-
кундах, x в сантиметрах. Найти амплитудные значения скорости и ускорения груза.
6. Шарик, висящий на пружине, неподвижен. Шарику толчком сообщили скорость v0 0, 4 м/с , направленную вертикально вниз, и одновременно начали отсчѐт времени. Найти амплитуду колебаний и записать закон изменения координаты x шарика. Ось x направлена вертикально вверх. Масса шарика m 0,1кг, жѐсткость пружины k 1,6Н/м.
7. Ускорение свободного падения на поверхности Марса 3,7 м/с2 . Как и во
сколько раз изменятся периоды колебаний математического и пружинного маятников на Марсе по сравнению с Землѐй?
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
28
2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
8. В колебательном контуре без затухания при свободных колебаниях максимальный ток в катушке индуктивности I0 66 мA , а максимальное напряжение
на конденсаторе U0 11 B . Ёмкость конденсатора C 0,36 мкФ . Найти индуктивность контура.
9.При каких условиях свободные колебания в колебательном контуре можно считать собственными?
10.При каких скоростях поезда можно ожидать особенно сильное раскачива-
ние шарика, подвешенного в вагоне на нити длиной l 80 см ? Расстояние между стыками рельсов L 20 м .
Задачи
1. Проводящий стержень MN длиной l расположен параллельно диагонали BD куба (рис. 22). Стержень движется поступательно с постоянной скоростью v вдоль ребра AB в постоянном однородном магнитном поле с индукцией B , направленной вдоль ребра B B . Найти ЭДС индукции в стержне.
|
|
|
|
|
R |
|
L |
|
A |
B |
B |
|
|
|
|
|
|
M |
|
|
|
|
|
D |
|
v |
|
|
|
|
|
C |
|
B |
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
N |
_ |
|
|
|
A |
B |
|
|
+ |
K |
|
|
|
|
|
||||
|
|
|
|
|
|||
D |
|
C |
|
O |
,r |
|
|
|
|
|
|
|
|||
|
Рис. 22 |
|
Рис. 23 |
Рис. 24 |
|||
2. Проводящий стержень вращается с угловой скоростью 300 с 1 вокруг
оси O в плоскости, перпендикулярной к силовым линиям магнитного поля с индукцией B 1 Тл (рис. 23). Одним концом стержень скользит по проводнику в
виде дуги окружности радиусом r 10 см . Между проводником и осью O включены батарея с ЭДС 4,5 B и резистор. Сопротивление резистора и внут-
реннее сопротивление батареи в сумме составляют R 15 Ом . Какой ток течѐт через резистор? Сопротивлениями стержня и проводника пренебречь.
3. В цепи (рис.24) R 37 Ом, r 3 Ом , 9 В, L 0, 03 Гн . С какой скоростью будет возрастать ток после замыкания ключа К в момент, когда ток достигнет значения I0 0, 075 A ?
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович
29

2012-2013 уч. год, №4, 11 кл. Физика. Электромагнитная индукция. Колебания
4. Катушка из n витков, площадь каждого из кото-
рых равна S , расположена в однородном магнитном |
B |
|
|
|
|
поле с индукцией B , которая направлена перпендику- |
|
|
лярно плоскости каждого витка катушки (рис. 25). Вне |
|
|
поля расположена вторая катушка. Обе катушки соеди- |
L1 |
L2 |
нены проводами. Пренебрегая омическим сопротивле- |
нием катушек и проводов, определить величину тока, возникающего в катушках после выключения поля. Ин-
дуктивности катушек L1 и L2 . (МФТИ, 1982)
5*. Конструкция (рис. 26) из жѐстко соединенных
лѐгкого стержня и небольшого шарика массой m может совершать колебания под действием двух пружин с жѐсткостями k1 и k2 , двигаясь при вращении без
трения вокруг вертикальной оси O по гладкой горизонтальной поверхности стола. Пружины лѐгкие, их оси горизонтальны, а точки их прикрепления к стержню делят его на три равные части. В положении равновесия оси пружин перпендику-
лярны стержню, и пружина с жесткостью k1 растянута на величину L1 .
1)Найти деформацию второй пружины в положении равновесия.
2)Найти период малых колебаний конструкции. (МФТИ, 1996)
|
|
|
|
|
|
k2 |
|
O |
|
m |
|||||
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 26 |
|
|
Рис. 27 |
|
6.На пружине жесткостью k висят два груза, связанные нитью (рис. 27). После пережигания нити верхний груз стал колебаться с
амплитудой A . Найти массу нижнего груза. (МФТИ, 1996)
7.Колебательный контур, состоящий из катушки ин-
дуктивности и конденсатора, через ключ K подключѐн к |
|
|
батарее с постоянной ЭДС и внутренним сопротивлением |
|
|
r (рис. 28). Первоначально ключ K замкнут. После уста- |
|
|
новления стационарного режима ключ размыкают, и в |
Рис. 28 |
|
контуре возникают колебания с периодом T . При этом |
||
|
||
|
|
|
2012, ЗФТШ МФТИ, Чивилѐв Виктор Иванович |
|
30
