3 Методика решения задачи

3.1 Общая структура модели

Поставленная задача должна решить следующие проблемы:

• Повысить надежность существующей кредитной политики банка и снизить кредитный риск.

• Сократить время на принятия решения банком

• Автоматизировать процесс принятия решения по клиенту

• Сравнить методы интеллектуального анализа данных

Анализ будет состоять из двух частей. Первая часть заключается в анализе базы данных клиентов банка, у которых имеется кредит. Скоринговая модель будет относится к типу поведенческого скоринга. Ключевым показателем является показатель списания клиента за первый год владения кредитным продуктом. Показатель в базе данных «Ever W/O @12 MOB» является показателем булевого типа. Результатом первого этапа будет набор параметром, полученный на обучающей выборке клиентов, которым банк выдал кредит в 2012 году. Второй этап это применение алгоритма к тестовой выборке за 2013 год. Третий этап заключается в применении полученных знаний и использования их для предложенного метода автоматизации принятия решения.

3.2 Основные этапы анализа данных

Можно выделить следующие основные этапы анализа данных:

• Подготовка данных для анализа.

Проведена нормализация данных: приведение параметров к булевому типу, числовому и текстовому, характеризующих данную область данных о клиенте. После выбора параметров, данные представляют собой прямоугольную таблицу, где каждая запись представляет клиента с набором характеристик, свойств и показателей.

• Из массива данных удалены данные, которые являются неинформативными, либо дублируют ключевой показатель.

Кроме того, сокращение количества полей позволяет сократить время обработки данных. Это позволяет избавиться от избыточности данных. База данных очищена от ошибок, дефектов и полей без значений.

• Применение методов поиска ассоциативных правил: алгоритм apriori, DHP, предикативный анализ.

• Верификация и проверка получившихся результатов.

• Использование полученной информации и применение ее в работе банка.

4 Формулировка задачи

4.1 Математическая формулировка

Модель алгоритма априори, его математическая составляющая описана в источниках [1-2]. Краткое обоснование используемых терминов и понятий дано ниже.

Правило X->Y имеет поддержку s (support), если s клиентов из D, содержат пересечение множеств X и Y. Достоверность правила показывает какова вероятность того, что из X следует Y. Правило X->Y справедливо с достоверностью c (confidence), если c транзакций из D, содержащих X, также содержат Y, conf(X-> Y) = supp(X->Y)/supp(X ).

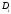
Рассмотрим принятую формальную постановку задачи поиска ассоциативных связей, введем базовые термины и опишем формализмы, используемые в существующей литературе по этой проблематике. 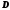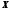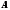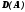Пусть –база данных клиентов банка, – произвольный клиент,–множество всех свойств и характеристик клиентов, которые используются для обозначения объектов в базе данных клиентов множества,–подмножество свойств и признаков из множестваX, и – подмножество множества данных клиентов из множества, каждая из которых содержит множество признаков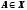в качестве подмножества. Для характеристики статистических свойств подмножестваA в базе данных обычно используют отношение мощности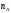множествак мощностивсего множества клиентов. Эту величину принято называть поддержкой (support) подмножества во множестве клиентов:

.

(1)

Порогом уверенности 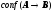=и порогом поддержки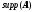=(,– ассоциативное правило) существуют, если справедливы следующие неравенства

, ,

(2)

где 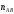– количество клиентов во множестве, которые содержат объединение множества символов подмножестви. Модель ассоциативного правила вида (2), принято называть моделью типа поддержка–уверенность. Подмножество элементовпринято называть посылкой правила, а подмножество– его следствием. Иногда эти подмножества называют паттернами (patterns). В задачах ассоциативной классификации заключение правила может содержать только однолитерный паттерн, например, метку одного из классов. Однолитерным может быть также и паттерн _. Те же обозначения и термины используются и при поиске ассоциативно или причинно связанных атрибутов. Задача поиска ассоциативных правил является здесь центральной задачей.

Кроме того, стоит отметить свойство антимонотонности. Поддержка любого набора элементов не может превышать минимальной поддержки любого из его подмножеств.  Данное свойство служит для снижения размерности пространства поиска. Не имей мы в наличии такого свойства, нахождение многоэлементных наборов было бы практически невыполнимой задачей в связи с экспоненциальным ростом вычислений.
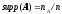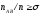
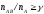