
- •Курс лекций по дисциплине: «Теория автоматического управления»
- •Динамическая система станка и ее основные элементы
- •Основные понятия и определения
- •Режимы работы системы
- •Обобщенная функциональная схема системы автоматического управления
- •Принципы управления
- •Классификация сау
- •Классификация саУпо свойствам в установившемся режиме.
- •Классификация сау по характеру внутренних динамических процессов
- •Классификация по виду внешних воздействий
- •Математическое описание линейных систем.
- •Статика систем управления
- •Динамика систем управления
- •Способы линеаризации систем автоматического управления
- •Операторный метод в тау
- •Основные свойства операторных преобразований, на примере оператора Лапласа.
- •Уравнение динамики в операторной форме
- •Уравнение динамики в стандартной форме
- •Типовые воздействия в тау
- •Частотные характеристики
- •Амплитудно-фазовая частотная характеристика
- •Логарифмические частотные характеристики.
- •Виды соединения систем. Правила преобразования структурных схем
- •Типовые динамические звенья.
- •Позиционные звенья
- •Механический колебательный контур
- •Интегрирующие звенья
- •Дифференцирующие звенья
- •Процесс резания как динамическое звено сау
- •Технические средства тау
- •Устойчивость линейных систем автоматического управления
- •Критерии устойчивости
- •Критерии Гурвица
- •Критерий Рауса
- •Частотные критерии устойчивости
- •Критерий Михайлова
- •Критерии Найквиста
- •Запасы устойчивости
- •Определение запасов устойчивости при лчх
- •Суждение об устойчивости систем по их структурной схеме
- •Управляемость и наблюдаемость систем автоматического управления.
- •Качества процесса управления Качество. Прямые и косвенные оценки качества
- •Прямые оценки качества переходного процесса
- •Косвенные оценки качества
- •Синтез систем ау
- •Применение обратных связей для улучшения динамических свойств системы
- •Применение лчх для синтеза сау
- •Применение лчх для синтеза.
- •Синтез систем с использованием лачх при последовательной коррекции
- •Синтез систем с помощью лачх при параллельной коррекции
- •Линейные импульсные системы Типы и основные элементы импульсных систем
- •Дискретное преобразование Лапласа.
- •Общая схема цифровых систем
- •Чпу станками. Системы чпу
- •Интерполяторы и их функции
- •Классификация систем чпу
- •Адаптивное управление технологическими процессами
- •Выбор источника информации по протеканию процесса
- •Управление точностью, за счет изменения размера статической настройки
- •Управление динамической настройкой станка
- •Управление износом инструмента
- •Нелинейные системы
- •Типовые однозначные нелинейности
- •Типовые неоднозначные
- •Фазовые методы исследования нелинейных систем
- •Виды особых точек
- •Автоколебательный режим
Применение обратных связей для улучшения динамических свойств системы
Для коррекции систем используют: жесткие и гибкие обратные связи.
Жесткие корректирующие обратные связи КОС обычно представлены позиционными элементами, как правило, безынерционного типа. Такие связи передают сигнал в любом режиме работы системы.
Гибкие корректирующие обратные связи обычно представлены дифференциальными звеньями КОСS (передняя функция). Такие связи передают сигнал только в переходном режиме.
Пример 1: охват безынерционного звена отрицательно жесткой обратной связью.
До охвата:

После:

![]() –сигнал ошибки
рассогласования
–сигнал ошибки
рассогласования
![]()
![]()
![]()
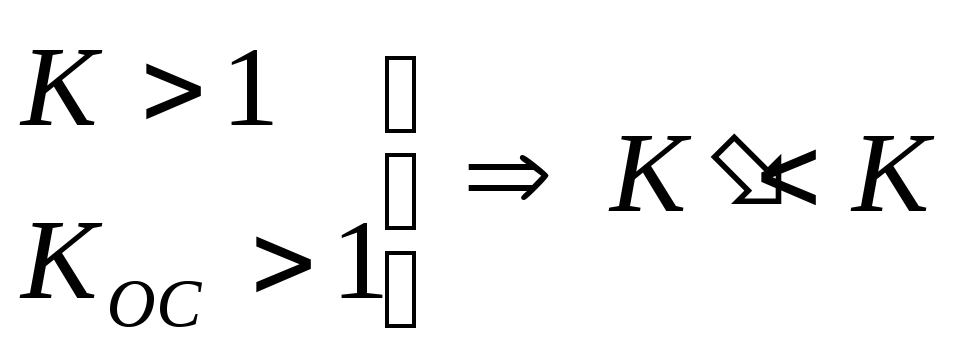
![]()
Сигнал на входе
повышается на 10%
![]() повышается на 10%
повышается на 10%
Пусть
![]()
Сигнал на входе
повышается на 10%
![]() сигнал на выходе стабилизируется.
сигнал на выходе стабилизируется.
Такая коррекция используется для стабилизации работы усилителей при колебании входного сигнала.
Пример 2: охват инерционного звена отрицательно жесткой обратной связи.

![]()
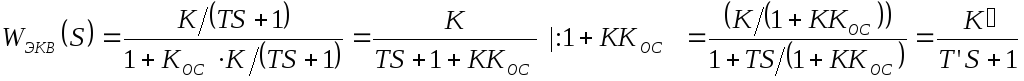
Звено не изменилось
![]() (т.к. К > 1)
(т.к. К > 1)
![]()
![]()
![]()
Данная коррекция является способом борьбы с инерционностью системы (превращает безынерционное звено в инерционное).
Пример 3: охват интегрирующего звена отрицательно жесткой обратной связью.

![]()
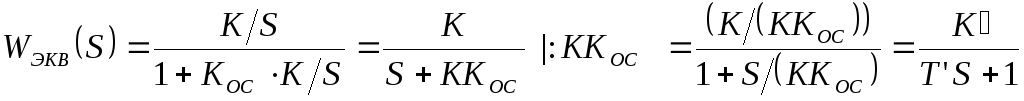
![]() –постоянная
времени = 1/ККОС
–постоянная
времени = 1/ККОС
Пример 4: охват безынерционного звена отрицательно гибкой обратной связью.

Представили:
![]() растет (из-за уменьшения нагрузки)
растет (из-за уменьшения нагрузки)![]() рост
сигнала обратной связи:z
растет; (
рост
сигнала обратной связи:z
растет; (![]() )
понижается
)
понижается![]()
![]() уменьшается.
уменьшается.![]() уменьшается
уменьшается![]()
![]() растет.
растет.
Такая коррекция используется для стабилизации выходного сигнала системы при колебании нагрузки.
Применение лчх для синтеза сау
Использование ЛЧХ для синтеза систем основано на наличии взаимосвязей между видом ЛЧХ и качественными показателями системы. Для вып-ия синтеза с помощью ЛЧХ первоначально строится ЛЧХ желаемой (скорректированной) системы. При построении такой характеристики принимается во внимание требования: точности системы, быстродействие, запасом устойчивости и колебательные свойства.
Желаемая ЛЧХ имеет 3 частотных области:
область низких частот,
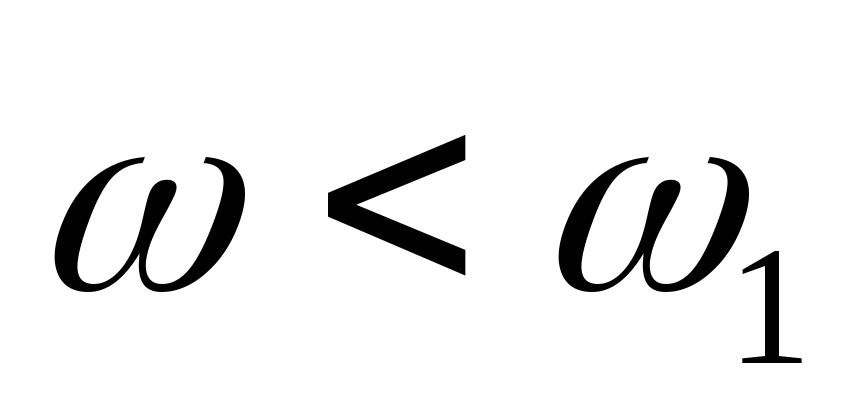
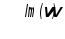 Данная
область обеспечивает требуемую точность
регулирования (К).
Данная
область обеспечивает требуемую точность
регулирования (К).
Область частот в интервале от наименьшей до наибольшей сопрягающей – средние частоты (СЧ). Вид ЛЧХ в этой области определяет быстродействие системы, её колебательные свойства и запасы устойчивости.
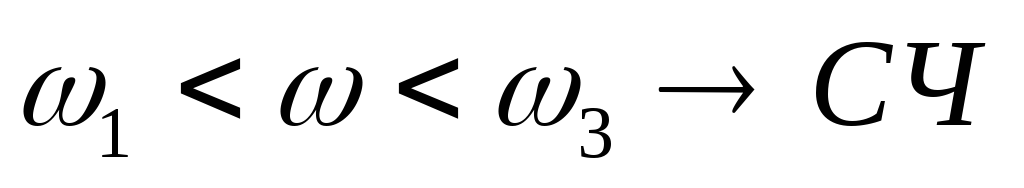
Частота среза
должна:
![]() ,
при этом она должна лежать на участке
ЛЧХ с наклоном -20Дб/дек. Желаемые
,
при этом она должна лежать на участке
ЛЧХ с наклоном -20Дб/дек. Желаемые![]() определяется с учетом требуемого времени
регулирования и допустимого
перерегулирования:
определяется с учетом требуемого времени
регулирования и допустимого
перерегулирования:
![]()
![]() –перерегулирование
–перерегулирование
![]()
1)
 границы
соответствующих частот области
границы
соответствующих частот области
2)
![]()
![]()
3) с учетом желаемых
запасов устойчивости;
![]()
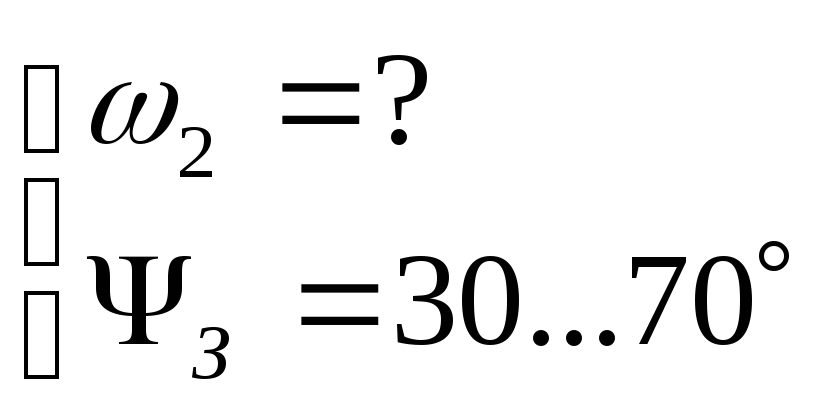
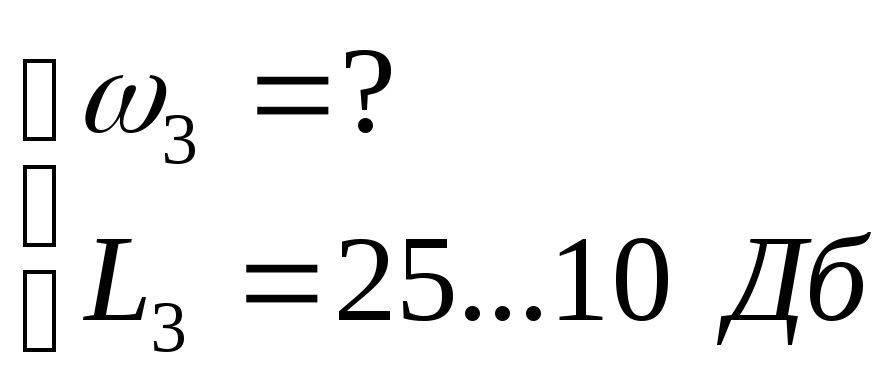
ВЧ – высокие частоты.
Вид ЛЧХ в этой области практически не влияет на свойства системы и поэтому ЛЧХ желаемой системы обычно соответствует ЛЧХ искомой системы.
Мое
Применение лчх для синтеза.
При разработке структуры АС прежде всего выбирают автоматический регулятор, его закон регулирования с учетом статических и динамических свойств регулирования. Если по закону регулирования наиболее подходящий регулятор не обеспечивает требуемого качества регулирования, то выбирают дополнительные функциональные устройства для коррекции динамических свойств системы или расчленяют на несколько контуров регулирования с использованием нескольких регуляторов и корректирующих устройств.
Корректирующие устройства могут подключаться последовательно, параллельно, тем самым, изменяя ее структуру. При необходимости в систему могут вводиться одновременно как параллельные, та и последовательные корректирующие устройства.
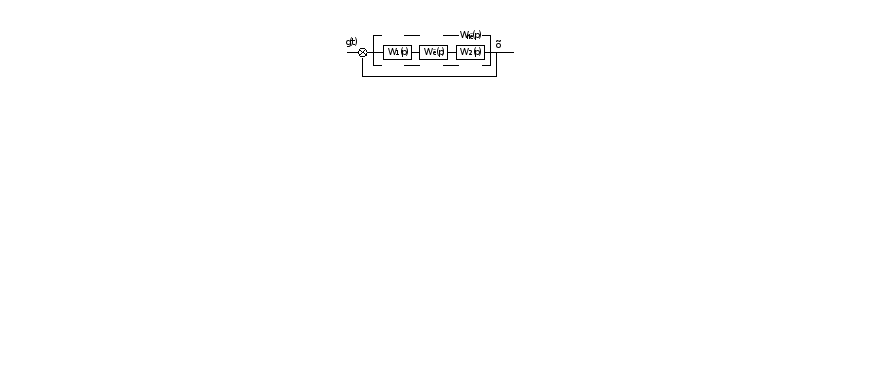
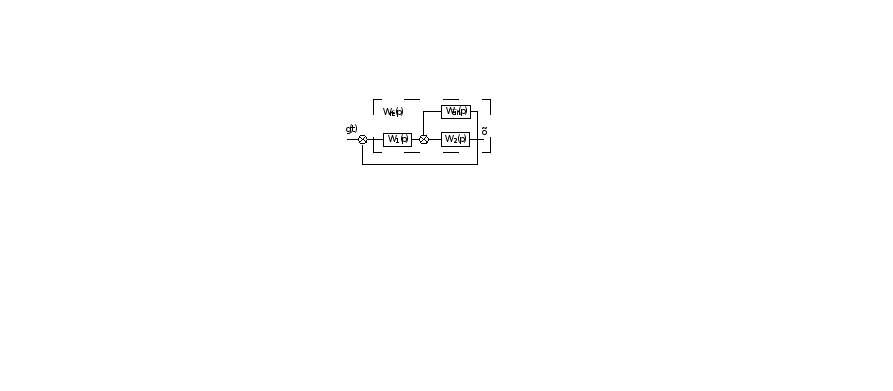
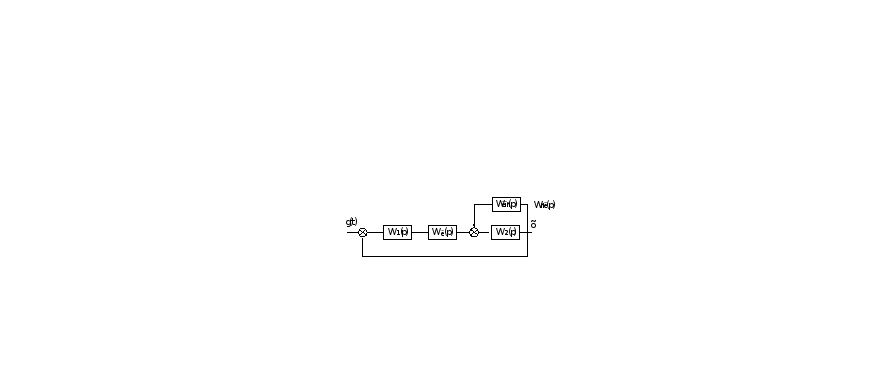
Передаточная функция системы с последовательным корректирующим элементом:
![]() (7.1)
(7.1)
где
![]() - передаточная функция разомкнутой
нескорректированной системы;
- передаточная функция разомкнутой
нескорректированной системы;
Wk – передаточная функция корректирующего устройства.
При требуемых динамических свойствах скорректированной системы, находим передаточную функцию последовательно корректирующего устройства.
![]()
Передаточная функция с параллельным корректирующим устройством имеет вид:
![]() (7.3)
(7.3)
Тогда передаточная функция корректирующего устройства:
![]()
При комбинированной коррекции необходимо сначала найти передаточную функцию корректирующего устройства обратной связи, исходя из требуемых динамических свойств системы, охваченной этим корректирующим устройством.
![]()
где Wck – желаемая передаточная функция части разомкнутой скорректированной системы с корректирующей обратной связью.
С учетом данных выражений находим требуемую передаточную функцию последовательного корректирующего устройства.
![]()
В качестве корректирующих устройств широкое применение находят типовые и комбинированные звенья.
Синтез требуемых корректирующих устройств наиболее удобно осуществлять с использованием ЛАЧХ.
В соответствии с (7.1) и рис.1 для последовательного соединения орректирующих элементов:
![]()
Логарифмируя данное выражение, находим желаемые ЛАЧХ последовательно корректирующего устройства.
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
С учетом данных выражений при последовательном включении корректирующего устройства синтез системы производят в следующем порядке:
1). строят логарифмические частотные характеристики исходной разомкнутой системы;
2). строят желаемые логарифмические частотные характеристики скорректированной системы;
3). с учетом выражений (7.8), (7.9) графически находят требуемые логарифмические частотные характеристики корректирующего устройства, по которым подбирают наиболее простое по техническому исполнению корректирующее устройство;
4). если частотные характеристики выбранного корректирующего устройства несколько отличаются от требуемых (расчетных), то необходимо построить ЛАЧХ скорректированной системы с учетом фактических логарифмических частотных характеристик корректирующего устройства и проверить на качество регулирования.
Для параллельного включения из выражения (7.3, рис. 2):
![]()
В интервале частот
![]() данное выражение приближенно можно
представить в виде:
данное выражение приближенно можно
представить в виде:
![]()
Отсюда следует, что в этом интервале частот параллельное корректирующее устройство практически не влияет на динамические свойства исходной системы.
В интервале частот
![]() можно написать
можно написать
![]() (7.13)
(7.13)
Отсюда следует, что в этом интервале частот влияние звеньев, охваченных корректирующим устройством в виде обратной связи, на динамические свойства системы практически исключаются.
Таким образом, корректирующую обратную связь следует в такие звенья системы, которые существенно ухудшают ее динамические свойства.
Логарифмируя выражение (7.13) находим
![]() (7.14)
(7.14)
![]() (7.15)
(7.15)
В выражениях (7.14, 7.15) известны ЛАЧХ исходной и скорректированной системы. Находя их разность графически, определяем суммарные ЛАЧХ корректирующего устройства и звеньев с корректирующим устройством.
Построив ЛАЧХ звеньев исходной системы с корректирующим устройством, графически находим требуемые ЛАЧХ корректирующего устройства.
По полученным частотным характеристикам корректирующего устройства подбирают наиболее простое в техническом отношении его исполнение. Если частотные характеристики выбранного корректирующего устройства несколько отличаются от расчетных, то необходимо построит ЛАЧХ скорректированной системы и проверить обеспечивается ли в системе требуемое качество регулирования. Если требуемое качество не обеспечивается, то можно дополнительно включить последовательно корректирующее устройство.
Прежде чем применить комбинированную корректирующую систему, целесообразно проверить возможность синтеза системы требуемого качества только с помощью последовательного корректирующего устройства вместо параллельного и наоборот.
Предположим, необходимо выполнить синтез САУ, ЛАЧХ представлена на рисунке.
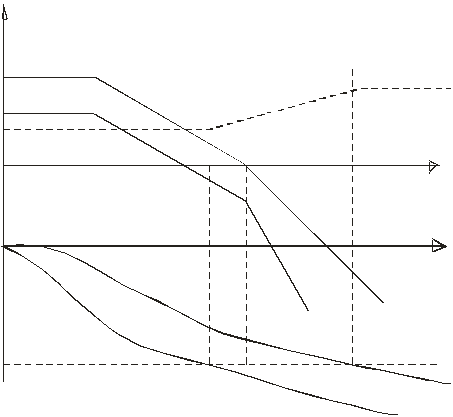
Допустим, что объект регулирования обладает такими динамическими свойствами, которые не дают возможность обеспечить требуемое качество регулирования. Исходя из требований к качеству регулирования, желаемая Lck(w) скорректированной системы имеет следующий вид.
В соответствии с
выражением
![]() вычитая из желаемойLck(w)
характеристику исходной системы L(w),
получаем ЛАЧХ корректирующего устройства
Lk(w).
вычитая из желаемойLck(w)
характеристику исходной системы L(w),
получаем ЛАЧХ корректирующего устройства
Lk(w).
Из анализа ЛАЧХ Lk(w) видно, что в качестве последовательного корректирующего устройства можно применить интегродифференцирующее звено.
