Моделирование типовых нелинейностей эп

К типовым нелинейностям электропривода относятся: «зона ограничения», «зона нечувствительности», «сухое трение», «модуль», делитель. Типовые нелинейности ЭП размещены в библиотеке нелинейных элементов Function Library, а их реализация в SV приведена в таблице 3.2.

Таблица 3.2 – Моделирование типовых нелинейностей

Нелинейность	Характеристика	Блок SV	Параметры блока
Зона ограничения			Input Max (V) = UВХ MAX Output Max (V) = UВЫХ MAX
		Limit
Зона нечувствительности			Dead Band (V) = U
		Dead Band
«Сухое трение»			Input Max (V) = 0 Output Max (V) =  MC
		Limit
Модуль			Zero Point = 0
		Rectify
Делитель	нет		Gain = 1
		Divide

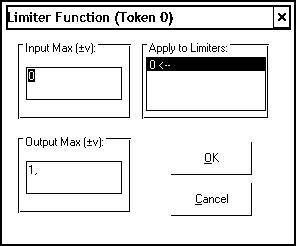
Блок Limit (ограничитель) имеет два параметра: Input Max – минимальное значение входного сигнала, при котором происходит ограничение и Output Max – максимальное значение выходного сигнала. Окно настройки ограничителя представлено на рисунке 3.6. Данный блок применяется для моделирования реактивной нагрузки и усилителей с ограничением.

Рисунок 3.6 – Окно настройки блока Limit

Блок Dead Band «зона нечувствительности» имеет один параметр – Dead Band – ширина зоны нечувствительности. Коэффициент наклона ветвей на линейном участке равен единице. Окно настройки блока Dead Band представлено на рисунке 3.7. Он применяется для моделирования люфта или зоны нечувствительности оборудования.

Рисунок 3.7 – Окно настройки блока Dead Band

Блок выделения модуля Rectify настраивается при помощи параметра Zero Point – смещение нуля по оси абсцисс.

Блок деления модуля Divide настраивается при помощи параметра Gain – коэффициент усиления. При включении блока в структурную схему необходимо задать вход делителя (Numerator) и делимого (Denominator).Окно настройки входов блока деления представлено на рисунке 3.8.

Рисунок 3.8 – Назначение входов блока Divide

Моделирование задающих воздействий

К типовым задающим воздействиям электропривода и автоматики относятся ступенчатое и линейно-нарастающее воздействия. Задающие или внешние воздействия сгруппированы в библиотеку внешних воздействий Source Library.

Задающее ступенчатое воздействие моделируется блоком Step Function. Настройка ступенчатой функции определяется тремя параметрами:

• Amplitude (V) – амплитуда выходного сигнала;

• Start time (s) – момент переключения от одного уровня к другому;

• Offset (V) – значение сигнала в начальный момент времени.

Окно настройки блока Step Function представлено на рисунке 3.9, а форма данного задающего сигнала представлена на рисунке 3.10.

Рисунок 3.9 – Внешний вид и окно настройки блока Step Function
Рисунок 3.10 – Выходной сигнал блока Step Function

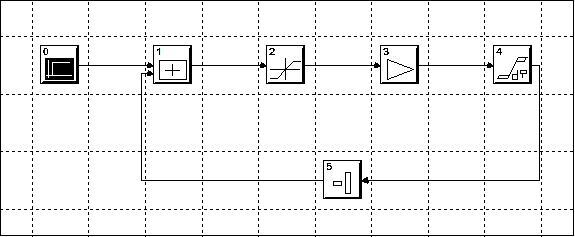
Модель линейно нарастающего задающего воздействия – задатчика интенсивности представлена на рисунке 3.11,а. В состав его модели входят блоки Step Function,Limit, Gain, Integrator и Negate. Блоки Gain и Integrator реализуют интегратор с регулируемой постоянной времени, которую задаёт блок Gain. Максимальное значение выходного сигнала определяет блок Limit. Блок Step Function формирует входной скачек задания.

а) модель задатчика интенсивности в System View

б) форма выходного сигнала задатчика интенсивности

Рисунок 3.11. Линейно нарастающее задающее воздействие

В таблице 3.3 представлены значения параметров указанных блоков для случая: время нарастания 2 секунды, установившееся значение 10В.

Таблица 3.3 – Значения параметров блоков

Наименование блока	Значения параметра блока
Step Function	Offset (V) = 0 В Amplitude (V) = 10 В Start Time (s) = 0 с
Limit	Input Max (V) = 0 В Output Max (V) = 10 В
Gain	Gain = 1/2
Integrator	Initial Condition (V) = 0 В

Моделирование нагрузок электропривода

К главным возмущениям систем электропривода относятся нагрузки, которые делятся на два вида: не зависящие и зависящие от величины скорости электропривода. К первому виду нагрузок относятся нагрузки активного и реактивного характера, а ко второму нагрузка типа «вязкое терние» и нагрузка вентиляторного характера.

Нагрузка активного характера обусловлена силой тяжести, которая действует на все тела и направлена вертикально вниз. Моделирование такой нагрузки выполняется с помощью блока Step Function. Механическая характеристика активной нагрузки представлена на рисунке 3.12,а, а параметры блока Step Function в таблице 3.4.

Нагрузка реактивного характера «сухое трение» обусловлена силой трения, которая всегда действует противоположно направлению движения. Моделирование такой нагрузки выполняется с помощью блока Limit и Dead Band. Скорость двигателя подаётся на вход блока Dead Band, а с него на блок Limit. Тогда при выборе параметров, как указано в таблице 3.4, знак момента сопротивления на выходе блока будет зависеть от скорости. Механическая характеристика реактивной нагрузки представлена на рисунке 3.12,б, а параметры блоков Limit и Dead Band в таблице 3.4.

а) активная	б) реактивная
Рисунок 3.12 – Нагрузки электропривода независящие от скорости движения

Нагрузка вентиляторного характера имеет место на валу двигателей турбомеханизмов: вентиляторов, дымососов, центробежных насосов. Механическая характеристика вентиляторной нагрузки представлена на рисунке 3.13. Момент сопротивления вентиляторного характера описывается следующей эмпирической зависимостью:

, (3.1)

где M₀ – момент сопротивления, обусловленный силами трения;

M_Н – момент сопротивления на валу двигателя;

_Н – номинальная скорость двигателя.

Рисунок 3.13 – Механическая характеристика вентиляторной нагрузки

Для моделирования вентиляторной нагрузки применяется блок Polynomialиз библиотеки нелинейных элементов, который реализует алгебраический полином пятого порядка:

. (3.2)

Внешний вид блока Polynomial и окно настройки параметров представлено на рисунке 3.14. а параметры блока Polynomial в таблице 3.4.

Рисунок 3.14 – Окно настройки полинома и внешний вид блока Polynomial

Таблица 3.4 – Значения параметров блоков для моделирования нагрузок

Наименование блока	Значения параметра блока
1	2
Step Function	Offset (V) = 0 В Amplitude (V) = 10 В Start Time (s) = 0 с
Limit	Input Max (V) = 0 В Output Max (V) = 10 В
Dead Band	Dead Band (V) = (0,5 – 3)% от рабочей скорости
Polynomial	x^5 Coeff, x^4 Coeff, x^3 Coeff, x^1 Coeff = 0; .

Моделирование регуляторов электропривода и систем управления

Замкнутой системой регулирования называется такая система, которая обеспечивает изменение регулируемой величины по требуемому закону. В такой системе используются канал задающей информации и канал обратной связи, по которому в систему управления поступает информация о текущем состоянии регулируемой величины.

Регулятор – это устройство, вырабатывающее на основании сигнала ошибки сигнал управления такой величины и знака, чтобы минимизировать ошибку регулирования. Все регуляторы можно условно подразделить на непрерывные, релейные (позиционные) и цифровые.

К непрерывным регуляторам, применяемым в системах автоматизации и управления электроприводами, относятся: пропорциональный (П – регулятор), интегральный (И – регулятор), пропорционально-интегральный (ПИ – регулятор) и пропорционально-интегрально-дифференциальный (ПИД – регулятор) регуляторы. Однако, вследствие более постой технической реализации наибольшее применение получили первые три типа регуляторов.

1. П – регулятор (пропорциональный)

Передаточная функция регулятора имеет вид:

, (3.3)

где k – коэффициент усиления регулятора.

2. И – регулятор (интегральный)

Передаточная функция регулятора имеет вид:

, (3.4)

где T_И – интегральная постоянная времени регулятора;

–интегральный коэффициент передачи регулятора.

3. ПИ – регулятор (пропорционально-интегральный)

Передаточная функция регулятора имеет вид:

, (3.5)

где k – коэффициент передачи регулятора;

T – постоянная времени регулятора;

T_И – интегральная постоянная времени регулятора.

Передаточные функции (3.3) – (3.5) представляют собой математическое описание регуляторов без учета насыщения, моделирование которых было рассмотрено в предыдущем разделе.

Выходной сигнал реального регулятора всегда ограничен уровнем питающего напряжения, разрядностью системы или допустимым уровнем выходного сигнала. На рисунке 3.15 представлена структурная схема модели ПИ – регулятора с насыщением, на основании которой легко получить П или И регулятор.

Рисунок 3.15 – Структурная схема модели ПИ – регулятора в System View

Модель (рис 3.15) имеет переменную структуру и её параметры различны при работе на линейном участке и в зоне ограничения. Параметры блоков, входящих в состав модели для различных типов регуляторов представлены в таблице 3.5.

Таблица 3.5 – Значения параметров блоков для моделирования регуляторов

Блок, номер	Назначение	Значение параметров блока
1	2	3
Gain (2)	Пропорциональный Коэффициент усиления	Gain = kП
Gain (4)	Интегральный коэффициент усиления	Gain = 1/TИ
Integrator (3)	Интегратор	Initial Condition (V) = 0 В
Switch (6, 12)	Ключ, изменяющий структуру модели	Thershold = 0,5
Negate (11)	Инвертор	нет
1	2	3
Limit (7)	Максимальное значение выходного сигнала	Input Max (V) = UВЫХ max Output Max (V) = UВЫХ max
Compare (15)	Компаратор (управляющий элемент)	True Output (V) = 1 В False Output (V) = 0 В Select Comparison “ = ”
Dead Band (8)	Зона нечувствительности (управляющий элемент)	Dead Band (V) = UВЫХ max
Full Rectify (9)	Блок выделения модуля (управляющий элемент)	Zero Point (V) = 0

Анализ результатов моделирования

Для просмотра и анализа результатов моделирования в System View имеются специальные блоки, объединенные в библиотеке элементов анализа Sink Library. Для вывода на экран или в окно анализа (рис. 3.16) какого-либо сигнала достаточно присоединить в требуемой точке модели один из элементов анализа. Блоки анализа и их характеристики сведены в таблицу 3.6.

Таблица 3.6 – Блоки анализа и их характеристики

Обозначение блока	Характеристика блока
	Analysis формирует вывод данных в окно анализа, не отображая их в рабочем окне
	System View обеспечивает вывод данных в окно анализа, а также их просмотр в рабочем окне
	External File организует запись данных во внешнем текстовом файле. Возможен просмотр графиков в окне анализа
	Data List формирует выходные данные в виде списка. Возможен просмотр графиков в окне анализа
	Real Time отображает просмотр данных в рабочем окне в реальном масштабе времени
	Final Value отображает в рабочем окне установившееся значение выходной величины

Рисунок 3.16 – Окно анализа

Выбор шага интегрирования

Важным вопросом при моделировании является правильный выбор шага интегрирования. Задание шага интегрирования, начального и конечного времени переходного процесса осуществляется в SV при помощи окна задания системного времени (рис 3.17).

Параметры окна задания системного времени

1. Start time – начальное время переходного процесса в секундах. Обычно при моделировании принимается равным нулю.

2. Stop time – конечное время переходного процесса в секундах. Определяется, исходя из динамических свойств моделируемой системы.

3. Sample rate – частота расчёта в герцах. Рекомендуется выбирать на порядок больше максимальной частоты в системе: .

4. Time spacing – шаг интегрирования в секундах: ; значение обратное частоте расчёта.

5. No. of Samples – число точек, в которых вычисляется переходной процесс.

6. No. of System Loops – организует повторный цикл моделирования. Если установлен ключ Reset system on Loop, то после каждого цикла сигналы на выходах блоков сбрасываются в нуль, иначе начальным значением последующего цикла моделирования становится конечное значение предыдущего цикла. Ключ Pause on Loop позволяет организовать паузу между циклами моделирования.

Рисунок 3.17 – Окно задания параметров системного времени