7. Закон ома для участка цепи, содержащего эдс

Закон Ома для участка цепи, содержащего ЭДС, позволяет найти ток этого участка по известной разности потенциалов на концах этого участка и имеющейся на этом участке ЭДС . Так из уравнения (1-13) имеем для схемы рис. 1-14, а

. (1-16)

Аналогично из уравнения (1-14) для схемы рис. 1-14, б следует

. (1-17)

Уравнения (1-16) и (1-17) выражают собой закон Ома для участка цепи, содержащего ЭДС, для разных случаев включения ЭДС .

8. Выражение потенциала люлой точки схемы через потенциалы соседних точек

Рассмотрим на примере схемы рис. 1-15.

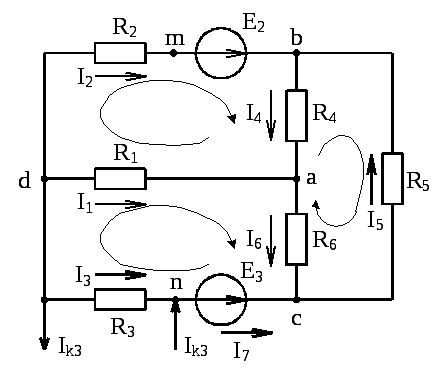
Рис. 1-15. Схема электрической цепи

Перед расчетом произвольно выбираются направления токов во всех ветвях и больше не меняются в процессе расчета.

Найдем разность потенциалов между точками d и n на пути ncabmd.

;

. (1-18)

При движении от точки n к точке c потенциал скачком возрастает на величину ЭДС . На участках ca и ab движемся против тока, т.е. в сторону возрастания потенциала, поэтому падения напряжения и входят в выражение (1-18) со знаком «плюс». Далее на участке bm скачок потенциала, поэтому падение напряжения входит в выражение (1-18) со знаком «плюс».

Разность потенциалов между точками d и n по кратчайшему пути будет:

U_dn = I₃R₃. (1-19)

Знак «плюс» соответствует возрастанию потенциала при движении от точки n к точке d по току.

Если при расчете по двум разным путям между одними и теми же точками получается одинаковая разность потенциалов, то можно считать, что токи рассчитаны верно. Это дополнительное средство проверки правильности расчета.

Найдем теперь разность потенциалов между точками b и m на пути mdncab:

U_bm = I₂R₂ – I₃R₃ + E₃ + I₆R₆ + I₄R₄; (1-20)

. (1-21)

9. Первый и второй законы кирхгофа. Составление уравнений для расчета токов в схемах при наличии в них источников эдс и тока

Первый закон Кирхгофа формируется следующим образом: алгебраическая сумма токов, сходящихся в узле равна нулю. Математически это записывается так:

. (1-22)

Здесь n – число узлов, для которых составляются уравнения по первому закону Кирхгофа.

Положительными считаются токи, подходящие к узлу, отрицательными – отходящие от узла.

В схеме рис. 1-15 пять узлов: a, b, c, d, n. Количество уравнений, которые нужно составить по первому закону Кирхгофа, равно числу узлов без единицы:

. (1-23)

Здесь У=5 число узлов.

Узлы, для которых составляются уравнения, выбираются произвольно.

Составим четыре уравнения по первому закону Кирхгофа для узлов a, b, c, d:

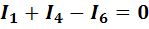1. ; (1-24)

b) ; (1-25)

c) ; (1-26)

d) - . (1-27)

Уравнение для последнего узла не составляется, так как оно может быть выведено из ранее составленных уравнений (1-24), (1-25), (1-26) и (1-27).

В схеме рис. 1-15 число ветвей В равно семи, оно всегда равно числу неизвестных токов.

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма падений напряжений вдоль любого замкнутого контура равно алгебраической сумме ЭДС того же контура.

. (1-28)

Здесь n – число контуров, для которых составляются уравнения по второму закону Кирхгофа.

Любой замкнутый путь в схеме называется электрическим контуром. Ветвь с источником тока не учитывается при подсчете числа контуров.

Так в схеме рис. 1-15 шесть контуров: admba, acnda, abca, cndabc, cadmbc и cndmbc.

Независимым контуром называется такой контур, в который входит хотя бы одна новая ветвь, не вошедшая в предыдущие контуры.

Независимых контуров на схеме рис. 1-15 всего три: admba, adnca, abca.

Контуры , и не являются независимыми контурами, так как входящие в них ветви уже использованы при составлении первых трех контуров.

Выберем также произвольно направления обхода независимых контуров, например, все по часовой стрелке.

Число уравнений , которые нужно составить по второму закону Кирхгофа равно числу ветвей минус , т.е. число уравнений, составленных по первому закону Кирхгофа

. (1-29)

Это всегда равно числу независимых контуров

. (1-30)

При составлении уравнений по второму закону Кирхгофа падение напряжения следует считать положительным, если направление тока в данной ветви совпадает с направлением обхода контура, и отрицательным – если ток не совпадает с направлением обхода.

Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:

admba ; (1-31)

abca ; (1-32)

acnda I₁R₁ + I₆R₆ – I₃R₃ = -E₃. (1-33)

ЭДС контура берутся со знаком «плюс», если их направления совпадают с направлением обхода контура, и «минус» - если не совпадают.

16