
МУ к выполнению КР
.pdf
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
ПО ЭКОНОМЕТРИКЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЯ 1
В задании 1 рассматривается парная линейная регрессия: y = a + b × x + ε .
Построение уравнения регрессии сводится к оценке его параметров. Для оценки параметров регрессий, линейных по параметрам, используется метод наименьших квадратов (МНК). Для линейного уравнения строится следующая система уравнений относительно параметров а и b:
или
где
a × n + b∑ x = ∑ y
∑ + ∑ 2 = ∑
a x b x yx
Его решение имеет вид:
b
= n∑ yx − (∑ y)(∑ x)
n∑ x 2 - (∑ x)2
b = yx - y × x ,
σ x2
a = y - b × x ,
y, x – средние значения результативного признака у и фактора х, σ2х –
дисперсия фактора х, п – объем выборки.
Тесноту связи между переменными в линейной регрессии оценивает линейный коэффициент парной корреляции:
σ x
ryx = b σ , (− 1 ≤ ryx ≤ 1).
y
Теснота линейной связи между переменными может быть оценена на основании шкалы Чеддока (см. табл. 1).
|
|
Таблица 1 |
|
Теснота связи |
Значение коэффициента корреляции при наличии: |
|
|
|
|
|
|
|
Прямой связи |
Обратной связи |
|
Слабая |
0,1–0,3 |
(–0,3)–(–0,1) |
|
Умеренная |
0,3–0,5 |
(–0,5)–(–0,3) |
|
Заметная |
0,5–0,7 |
(–0,7)–(–0,5) |
|
Высокая |
0,7–0,9 |
(–0,9)–(–0,7) |
|
Весьма высокая |
0,9–1 |
(–1)–(–0,9) |
|
|
|
1 |
|

Коэффициент детерминации R2 определяется как квадрат показателя корреляции (линейного коэффициента) и имеет смысл доли факторного среднего квадратического отклонения (СКО) в общем СКО:
R 2 = ∑ ((y x - y))2 ,
∑ y - y 2
здесь yx – значение результативного признака, рассчитанное по уравнению регрессии при подстановке в него заданных значений х.
R2 характеризует качество подгонки кривой под измеренные значения у и изменяется от 0 до 1. В пределе при R2=1 уравнение регрессии точно аппроксимирует заданные значения, то есть все точки на графике точно ложатся на регрессионную кривую, остаточное СКО равно нулю. Другое предельное значение, R2=0, означает, что уравнение регрессии ничего не дает по сравнению с тривиальным предсказанием y = y , и остаточное СКО равно общему; при этом факторное СКО равно нулю. Однако обычные значения R2 находятся между нулем и единицей. Для констатации хорошего качества подготовки кривой нужно, чтобы значение R2 было не меньше 0,8. Ошибка аппроксимации для каждого измеренного значения у определяется как относительная (выраженная в процентах) разность между значением у и значением yx , полученным по уравнению регрессии:
Ai = |
|
yi |
- yx |
|
×100 . |
|
|
||||
|
|
i |
|
||
|
yi |
||||
|
|
|
|
|
Осреднение этой величины по всем измеренным значениям у дает среднюю ошибку аппроксимации:
A = 1n ∑ Ai .
Таким образом, эта величина характеризует среднее отклонение расчетных значений от фактических. Она должна составлять не более 8-10%. Большее значение свидетельствует о плохом качестве аппроксимации.
По уравнению регрессии можно определить значение коэффициента эластичности. Для линейного уравнения этот коэффициент рассчитывается следующим образом:
=b × x
Эa + b × x .
Средний коэффициент эластичности получается при подстановке в формулу среднего значения фактора x.
Статистическая надежность уравнения регрессии в целом оценивается с помощью F-критерия Фишера:
2

Fфактич = Dфакт . Dостат
В числителе и в знаменателе этого выражения стоят значения СКО на одну степень свободы (то есть дисперсии на одну степень свободы). Факторная дисперсия имеет одну степень свободы и не отличается от значения факторной СКО:
Dфакт = ∑ (yx − y)2 .
1
Остаточная дисперсия имеет число степеней свободы, равное (n-2):
Dостат = |
∑ (y − y x )2 |
. |
|
|
n − 2 |
При анализе достоверности уравнения регрессии в целом фактическое |
|
значение F-критерия сравнивается |
с табличным, которое берется при |
некотором уровне значимости (например, 0,05) и двух степенях свободы – числителя, равной 1, и знаменателя, равной (n-2): Fтабл = F (α ;1; n − 2).(см. таблицу значений F-критерия Фишера).
Далее выдвигается нулевая гипотеза Но том, что остаточная дисперсия равна факторной, то есть Dфакт = Dостат . Это эквивалентно утверждению
статистической незначимости уравнения регрессии. Альтернативная гипотеза Н1 говорит о том, что факторная дисперсия превосходит остаточную, что и означает обоснованность предложенного уравнения и статистическую значимость связи между у и х.
Если Fфакт < Fтабл , Но не отвергается (то есть принимается), и уравнение
регрессии считается статистически незначимым. В противном случае, то есть Fфакт > Fтабл превышение факторной дисперсии над остаточной считается
неслучайным, и Но отвергается. При этом принимается H1, уравнение регрессии признается статистически значимым.
Прогнозное значение результативного признака y p получается при подстановке в уравнение регрессии прогнозного значения фактора xp .
Доверительный |
интервал прогноза |
значения |
y p для вероятности |
1 − α |
|
определяется по выражению: |
|
|
|
|
|
|
(y p - my p × tтабл ; y p + my p |
× tтабл ). |
|
||
Значение |
tтабл определяется по |
таблице |
t-распределения Стьюдента |
||
t(α; n − 2) при |
уровне значимости |
α |
и числе степеней свободы |
(n − 2) |
|
Стандартная ошибка прогноза определяется по формуле:
3

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(x p |
− |
|
|
|
|
)2 |
|
|
|
m y |
= σ ост |
1 + |
+ |
x |
, |
||||||||||||
n |
∑ (x − |
|
|
)2 |
|||||||||||||
p |
|
|
|
|
|
|
x |
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
σ ост. = |
|
|
|
∑(y − yˆ x )2 |
|
|
|
|||||||||
|
|
|
|
|
|
n − 2 |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение задач парной регрессии и корреляции с помощью ППП
MS Excel
Рассмотрим решение эконометрических задач с помощью встроенных функций MS Excel. Активизируем Мастер функций любым из способов:
–в главном меню выбрать Вставка / Функция;
–на панели инструментов Стандартная щелкнуть по кнопке fx
Вставка функции.
Для вычисления выборочных средних используем функцию
СРЗНАЧ(число 1:число N) из категории Статистические.
Выборочная ковариация между x и y находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.
Выборочные дисперсии определяются статистической функцией
ДИСПР(число 1:число N).
Выборочный коэффициент корреляции между x и y вычисляется с
помощью статистической функции КОРРЕЛ(массив X;массив Y).
Параметры линейной регрессии y = a + bx в Excel можно определить несколькими способами.
Cпособ 1. С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1.Выделить область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 – для получения только коэффициентов регрессии.
2.С помощью Мастера функций среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 1):
4
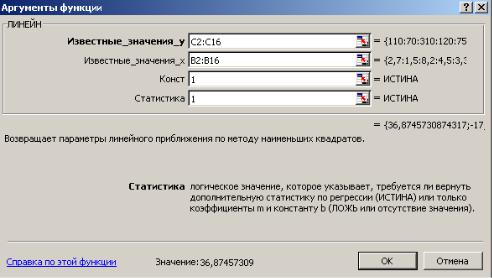
Рис. 1. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.
Дополнительная регрессионная |
статистика будет выведена в виде |
|
(табл. 2): |
|
|
|
|
Таблица 2 |
Значение коэффициента b |
|
Значение коэффициента a |
Среднеквадратическое |
|
Среднеквадратическое |
отклонение b |
|
отклонение a |
Коэффициент |
|
Среднеквадратическое |
детерминации R2 |
|
отклонение y |
F -статистика (Fфакт ) |
|
Число степеней свободы |
|
|
|
Регрессионная сумма квадратов |
|
Остаточная сумма квадратов |
Способ 2. С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа,
5
доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
1.Необходимо проверить доступ к Пакету анализа. Для этого в главном меню нужно выбрать Сервис / Настройки и напротив Пакета анализа установить флажок.
2.Выбрать в главном меню Сервис / Анализ данных / Регрессия и
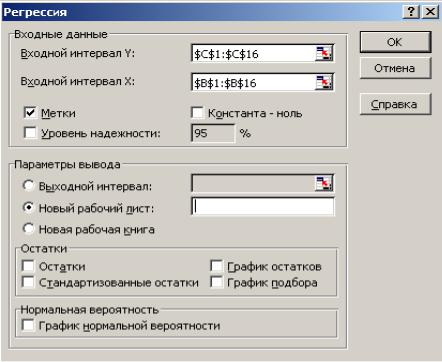
заполнить диалоговое окно (рис. 2):
Входной интервал Y – диапазон, содержащий данные результативного признака Y;
Входной интервал X – диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне. В результате получим итоги как на рис. 3.
Рис. 2. Диалоговое окно ввода параметров инструмента Регрессии
6

|
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Регрессионная статистика |
|
|
|
|
|
|
|
||
|
Множественный R |
0,9595 |
|
|
|
|
|
|
|
|
|
R-квадрат |
|
0,9206 |
|
|
|
|
|
|
|
|
Нормированный |
|
|
|
|
|
|
|
|
|
|
R-квадрат |
|
0,9145 |
|
|
|
|
|
|
|
|
Стандартная ошибка |
35,6056 |
|
|
|
|
|
|
|
|
|
Наблюдения |
|
15 |
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
||
|
Регрессия |
1 |
191102,5 |
191102 |
150,74 |
1,59E-08 |
|
|
|
|
|
Остаток |
13 |
16480,86 |
1267,76 |
|
|
|
|
|
|
|
Итого |
14 |
207583,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стан- |
|
|
|
|
|
|
|
|
|
Коэффи- |
дартная |
t-ста- |
P-Значе- |
Нижние |
Верхние |
Нижние |
Верхние |
|
|
|
циенты |
ошибка |
тистика |
ние |
95% |
95% |
95,0% |
95,0% |
|
|
Y- |
|
|
|
|
|
|
|
|
|
|
пересечение |
-17,781 |
19,3787 |
-0,9175 |
0,3756 |
-59,6461 |
24,084 |
-59,6461 |
24,084 |
|
|
x |
36,875 |
3,0034 |
12,2776 |
1,6E-08 |
30,3861 |
43,363 |
30,3861 |
43,363 |
|
Рис. 3. Результаты применения инструмента Регрессия
В Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1.Необходимо выделить область построения диаграммы и в главном меню выбрать Диаграмма / Добавить линию тренда.
2.В появившемся диалоговом окне (рис. 4) выбрать вид линии тренда и задать соответствующие параметры.
Рис. 4. Диалоговое окно типов линии тренда Для полиноминального тренда необходимо задать степень
7
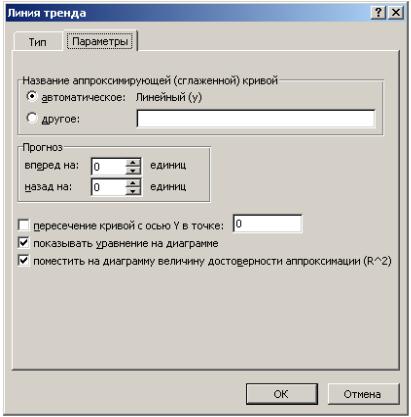
аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии. В качестве дополнительной информации можно показать уравнение на
диаграмме и поместить на диаграмму величину R2 , установив соответствующие флажки на закладке Параметры (рис. 5).
В результате получим линейный тренд (рис. 6).
Рис. 5. Диалоговое окно параметров линии тренда
8
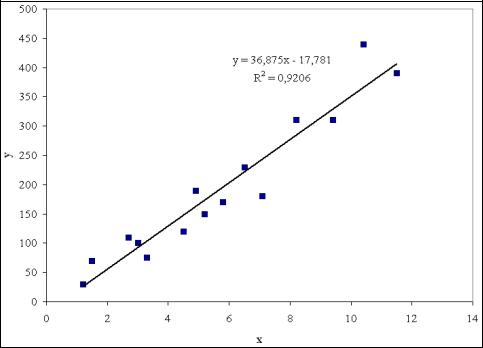
Рис. 6. Линейный тренд
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ 1
По семи территориям Уральского района за 200Х г. известны значения двух признаков:
Район |
Расходы |
на |
покупку |
Среднедневная заработная |
|
продовольственных |
плата одного работающего, |
||
|
товаров в общих расходах, |
руб., (х) |
||
|
% (у) |
|
|
|
Удмуртская |
|
68,8 |
|
45,1 |
республика |
|
|
|
|
Свердловская обл. |
|
61,2 |
|
59,0 |
Башкортостан |
|
59,9 |
|
57,2 |
Челябинская обл. |
|
56,7 |
|
61,8 |
Пермская обл. |
|
55,0 |
|
58,8 |
Курганская обл. |
|
54,3 |
|
47,2 |
Оренбургская обл. |
|
49,3 |
|
55,2 |
1.Рассчитать параметры парной линейной регрессии.
2.Оценить тесноту связи с помощью показателей корреляции и детерминации.
3.Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
9
4.Оценить с помощью средней ошибки аппроксимации качество уравнений.
5.Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
6.Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α =0,05.
Решение.
Для расчета параметров а и b линейной регрессии у = а + bх решаем систему нормальных уравнений относительно а и b:
an + b∑ x = ∑ y,
a∑ x + b∑ x 2 = ∑ yx
По исходным данным рассчитываем значение всех сумм (см. табл. 3).
Таблица 3
N |
y |
x |
ух |
x2 |
y2 |
y x |
y − y x |
Ai |
п/п |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
68,8 |
45,1 |
3102,88 |
2034,01 |
4733,44 |
61,3 |
7,5 |
10,9 |
2 |
61,2 |
59,0 |
3610,80 |
3481,00 |
3745,44 |
56,5 |
4,7 |
7,7 |
3 |
59,9 |
57,2 |
3426,28 |
3271,84 |
3588,01 |
57,1 |
2.8 |
4,7 |
4 |
56,7 |
61,8 |
3504,06 |
3819,24 |
3214,89 |
55,5 |
1,2 |
2,1 |
5 |
55,0 |
58,8 |
3234,00 |
3457,44 |
3025,00 |
56,5 |
-1,5 |
2,7 |
6 |
54,3 |
47,2 |
2562,96 |
2227,84 |
2948,49 |
60,5 |
-6,2 |
11,4 |
7 |
49,3 |
55,2 |
2121,36 |
3047,04 |
2430,49 |
57,8 |
-8,5 |
17,2 |
∑ |
405,2 |
384,3 |
22162,34 |
21338,41 |
23685,76 |
405,2 |
0,0 |
56,7 |
Определяем значение параметра b:
b = |
n∑ yx − (∑ y)(∑ x) |
= |
7 × 22162,34 - 384,3 × 405,2 |
= -0,35 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
7 × 21338,41 - 384,32 |
||||||
|
|
|
|
|
|
|
n∑ x2 − (∑ x)2 |
|
|||||||
Среднее значение переменных: |
|
||||||||||||||
|
|
|
= |
1 |
|
∑ y = |
405.2 |
= 57.89 . |
|
||||||
|
y |
|
|||||||||||||
|
|
n |
|
|
|
||||||||||
|
|
|
|
|
|
7 |
|
|
|
|
|
||||
|
|
= |
1 |
|
∑ x = |
384.3 |
= 54.9 . |
|
|||||||
x |
|
||||||||||||||
|
n |
|
|
|
|||||||||||
|
|
|
|
|
|
7 |
|
|
|
|
|
||||
С их помощью определим параметр а:
10
