Комплексное сопротивление элемента (участка цепи)

Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:

. (1.6)

где Z –модуль комплексного сопротивления, φ=ψ_u - ψ_i – начальная фаза или аргумент комплексного сопротивления; R - активного сопротивления, X– реактивному сопротивлению, причем Z=(R²+X²)^1/2, а φ_z(ω)=ψ_u-ψ_i =arctg(X/R).

По виду записи комплексного сопротивления можно судить о характере участка цепи: Z=R – активное (резистивное) сопротивление; Z=R+jX — активно-индуктивное сопротивление; Z=R – j X — активно-емкостное

- комплексная проводимость, величина, обратная комплексному сопротивлению:

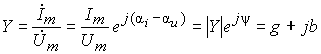
Метод комплексных амплитуд состоит в следующем:

1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:

а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.

б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е.х(t) =X_m cos(₀t – _x) X_m =X_m e^–jx.

R

Z_R=R

C

Z_C=1/(jC)

L

Z_L=jL

Рис. 4.27

2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождениюкомплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е.Y_m = Y_m e^–jy.

3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.

Y_m=Y_m e ^–jy  y(t) =Y_m cos(₀t – _y).

Пример 5. Алгоритм метода рассмотрим на примере анализа цепи, структура которой приведена на рис. 4.29.

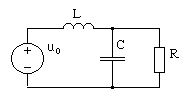
Рис. 4.29. RLC-цепь второго порядка

На вход цепи подается синусоидальное воздействие . Параметры воздействия и элементов цепи известны:U_m=1 В, ω =1 с^-1 , φ _u=90⁰ , R=1 Ом, L=1 Гн, C=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.

Решение.

1. Представим воздействие в комплексной форме:

.

2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.

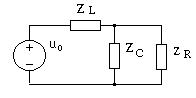
Рис. 4.30. Схема замещения цепи в частотной области

3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:

, ,,

,

, ,

,

, .

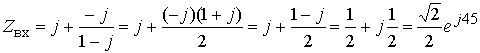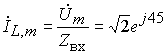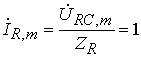3. Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.

Рис. 4.31. Векторная диаграмма

 Построение векторной диаграммы, как правило, является конечным результатом решения подобных задач. Векторная диаграмма показывает амплитуду и начальную фазу любого тока или напряжения. При необходимости записать временную функцию тока или напряжения, это всегда можно сделать, имея векторную диаграмму. Например, напряжение на L-элементе имеет амплитуду , а начальную фазу 135⁰, значит, во временной области это напряжение можно записать так:

.

Пример 2.

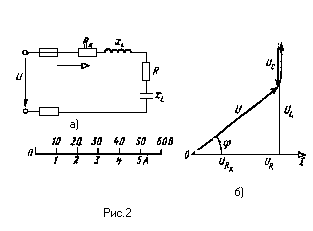
Активное сопротивление катушки R_к=6 Ом, индуктивное X_l=10 Ом. Последовательно с катушкой включено ативное сопротивление R=2Ом и конденсатор сопротивлением х_с=4 Ом (рис.2,а). К цепи приложено напряжение U=50В ( действующее значение). Определить :1) полное сопротивление цепи;2)ток;3)коэффициент мощности;4)активную, реактивную и полную мощности;5) напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи.

Решение:

1.Определяем полное сопротивление цепи

2.Определяем ток

3.Определяем коэффициент мощности цепи

по таблицам Брадиса находим =36⁰50’ . Угол сдвига фаз  находим по синусу во избежание потери знака угла ( косинус является четной функцией)

4.Определяем активную мощность цепи

или

Здесь

5.Определяем реактивную мощность цепи

6.Определяем активную мощность цепи

или

7.Определяем падение напряжения на сопротивлениях цепи

; ;;

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току : в 1см – 1,0А и масштабом по напряжению : 1см- 10В. Построение векторной диаграмм ( рис.2,.б) начинаем с вектора тока, который откладываем по горизонтали в масштабе

Вдоль вектора тока откладываем векторы падения напряжения на активных сопротивления U_Rк и U_R:

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90⁰ вектор падения напряжения U_L на индуктивном сопротивлении длиной .Из конца вектораU_I откладываем в сторону отставания от вектора тока на 90⁰ вектор падения напряжения на конденсаторе U_C длиной . Геометрическая сумма векторовU_Rк, U_R, U_L и U_C равна полному напряжению U, приложенному к цепи .

Пример 3.

На рис. 3,а задана векторная диаграмма для неразветвленной цепи, ток I и падения напряжений на каждом сопротивлении ( U₁, U₂ и т.д.) Определить характер и величину каждого сопротивления, начертить эквивалентную схему цепи, вычислить приложенное напряжение и угол сдвига фаз .

Решение:

1.Из векторной диаграммы следует, что напряжение U₁ отстает от тока на угол 90⁰. Следовательно, на первом участке включен конденсатор, сопротивление которого

Вектор напряжение на втором участке U₂ направлен параллельно вектору тока, т.е. совпадает с ним по фазе. Значит, на втором участке включено активное сопротивление

Вектор напряжения на третьем участке U₃ опережает вектор тока на угол 90⁰, что характерно для индуктивности, сопротивление которой

На четвертом участке включено активное сопротивление

Эквивалентная схема цепи приведена на рис. 3, б.

2.Из векторной диаграммы определяем значение приложенного напряжения и угол сдвига фаз:

.

Пример:

К электрической цепи, рис. 3.12, а, подведено синусоидальное напряжение частотой f = 50 Гц с действующим значением U = 100 В. Параметры элементов схемы: R₁ = 30 Ом, L = 0,1 Гн, C = 50 мкФ, R₂ = 20 Ом. Определить токи в ветвях схемы и показания приборов. Составить баланс мощности. Построить в масштабе векторную диаграмму токов и напряжения.

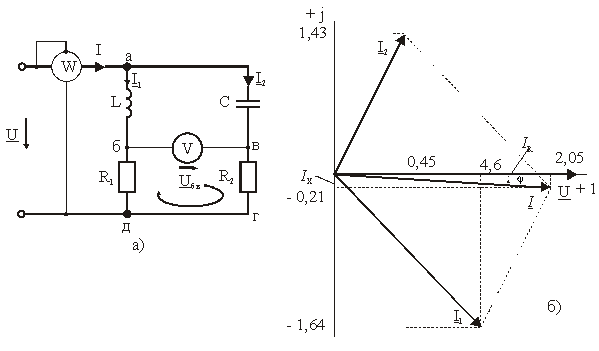Рис. 3.12 – Параллельная цепь: а) схема замещения; б) векторная диаграмма

Решение

Определяем комплексные сопротивления параллельных ветвей. Сопротивление первой ветви

Z₁ = R₁ + jX_L,

где

X_L = jωL = 2πfL = 6,28∙50∙0,1 = 31,4 Ом;

Z₁ = 30 + j31,4 Ом.

Комплексное сопротивление второй ветви

Z₂ = R₂ – jX_С;

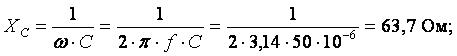
Z₂ = 20 – j63,7 Ом.

Находим комплексные значения токов в ветвях

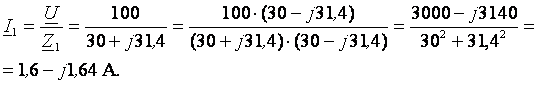
I = I₁ + I₂ = 1,6 – j1,64 + 0,45 + j1,43 = 2,05 – j0,21 A.

Действующие значения

Для определения показания вольтметра составляем уравнение согласно второго закона Кирхгофа для контура б, в, г, д, б. Произвольно выбираем направление обходе контура, показанное на рис. 3.12, а стрелкой

0 = U_бв + R₂I₂ – R₁I₁;

1. . U_бв = R₂I₂ – R₁I₁ = 20·(0,45 + j1,43) – 30(1,6 – j1,64) =

= 9 + j28,6 – 48 + j49,2 = - 39 + j77,8;

U_бв = 39 – j77,8 В.

Вольтметр покажет действующее значение напряжения U_бв

Ваттметр измеряет мощность, потребляемую активной нагрузкой (R₁ и R₂).

Известно, что

Р = U·I·cosφ.

В этом выражении неизвестным является cosφ, где φ угол сдвига между напряжением U и током I. Определить угол φ (или cosφ) можно разными путями. Например, cosφ можно найти из выражения для общего тока, учитывая, что начальная фаза напряжения равна нулю. Для этого обратимся к комплексному значению общего тока

I = 2,05 – j0,21 A,

где I_R = 2,05 – активная составляющая тока (проекция комплексного вектора полного тока на ось действительных чисел);

I_X = - j0,21 – реактивная составляющая тока (проекция комплексного вектора полного тока на ось мнимых чисел).

Тогда

где I = 2,06 А – действующее значение общего тока.

Показание ваттметра

Р = 100∙2,06∙0,995 = 205 Вт.

Составим баланс мощностей.

Полная мощность, поступающая от источника

где P_И = 205 Вт; Q_И = 21 Вар.

Мощности приёмников

S_П = Р_П + jQ_П = 205 + j21,34 ВА.

Результаты расчётов показывают, что баланс мощности сходится, т. е. токи найдены правильно.

Векторную диаграмму строим на комплексной плоскости, рис. 3.12, б. Выбираем масштабы тока и напряжения: (Масштаб выбирается с таким расчётом, чтобы векторная диаграмма занимала примерно половину страницы). Откладываем вектор напряжения совпадающий с осью+1. Затем откладываем вычисленные значения токов I₁, I₂, I. Действительные значения – на оси +1, мнимые значения – на оси +j.

Контрольные вопросы к экзамену (зачету)

Контрольные вопросы к зачету (экзамену ) по разделу "Основы электротехники".

1. Электробезопасность. Характеристики поражения человека электрическим током.

2. Основные определения: электротехника, электричество, электрическое поле, потенциал, напряжение, электрический ток, источники тока , электродвижущая сила (ЭДС), закон Ома , законы Кирхгофа.

3. Электрическая цепь. Пассивные и активные элементы цепи. Параметры электрической цепи.

4. Расчет электрических цепей постоянного тока методом законов Кирхгофа, методом контурных токов.

5. Энергия и мощность постоянного тока. Баланс мощностей.

6. Переменный ток. Однофазный синусоидальный ток. Основные параметры: мгновенные, действующие и средние значения тока, напряжения и ЭДС. Генерирование переменного тока.

7. Представление переменного тока комплексными величинами. Метод комплексных диаграмм.

8. Метод комплексных амплитуд. Закон Ома и законы Кирхгофа в комплексной форме.

9. Активное сопротивление, индуктивность и емкость в цепи переменного тока.

10. Последовательная и разветвленные цепи переменного тока с активным сопротивлением, емкостью и индуктивностью. Резонанс тока. Резонанс напряжения.

11.Мощность и энергия в цепи переменного тока. Активная, реактивная и полная мощность. Единицы измерения. Баланс мощностей.

12.Трехфазные электрические цепи. Основные определения. Линейные и фазные токи и напряжения. Маркировка фазы. Способы соединения генераторов и приемников типа звезда и треугольник. Трехпроводные и четырехпроводные цепи. Нейтральный провод.

13. Короткое замыкание фазы. Разрыв линейного провода. Мощность в цепи трехфазного тока.

14. Нелинейные электрические цепи. Аппроксимация нелинейных характеристик.

15. Расчет цепей постоянного тока с одним или несколькими нелинейными элементами.

16. Основные магнитные величины. Магнитные цепи постоянного тока.

17. Магнитные цепи переменного тока. Ферромагнитные материалы.

18. Расчет катушки с магнитопроводом и воздушным зазором.

19. Энергия и основные потери в магнитопроводе.

20 Трансформатор. Основные режимы работы.

21. Устройство и принцип действия машин постоянного тока.

22. Генератор постоянного тока. Основные характеристики.

23.Двигатель постоянного тока. Основные характеристики.

24.Устройство и принцип действия машины переменного тока.

25. Асинхронный двигатель. Основные характеристики.

26. Синхронный генератор. Основные характеристики.

Темы рефератов.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Самостоятельная работа студентов состоит в изучении ряда теоретических вопросов по темам дисциплины, перечень которых приведен в таблице 5 и составления рефератов..

Таблица 5

№ п/п	Тема дисциплины
1	2
1	Тема 1. Электрические цепи. Основные определения, топологические параметры
2	Тема 2. Методы расчета линейных электрических цепей
3	Тема З. Однофазный переменный ток
4	Тема 4. Электрические цепи трехфазного тока.
5	Тема 5. Магнитные цепи и электромагнитные устройства.
6	Тема 6. Трансформаторы
7	Тема 7. Асинхронные машины
8	Тема 8. Машины постоянного тока (МПТ)
9	Тема 9. Синхронные машины
10	Тема 10. Электрические измерения и приборы
11	Тема 11. Основы электроники и элементной базы современных электронных устройств
12	Тема 12. Источники вторичного электропитания
13	Тема 13. Усилители электрических сигналов
14	Тема 14. Импульсные и автогенераторные устройства
15	Тема 15. Основы цифровой электроники
16	Тема 16. Микропроцессорные средства