2.5.1. Метод непосредственного применения законов Кирхгофа

Пример . Методом непосредственного применения законов Кирхгофа рассчитать токи в схеме на рис.

Число ветвей обозначим m, а число узлов n. Произвольно выбираем положительные направления токов в ветвях и направления обхода контуров. Поскольку в каждой ветви протекает свой ток, то число токов, которое следует определить, а следовательно, и число уравнений, которое нужно составить, равно m. По первому закону Кирхгофа составляем n-1 уравнений. Недостающие m-(n-1) уравнений следует составить по второму закону Кирхгофа для взаимно независимых контуров.

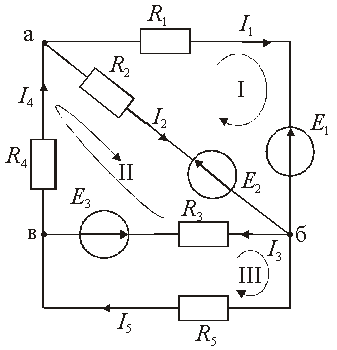Рис. 2.20. Схема замещения сложной электрической цепи с несколькими источниками энергии: I, II, III – номера контуров

1. Проводим топологический анализ.

Она содержит пять ветвей и три узла, m = 5, n = 3. Составляем два уравнения по первому закону Кирхгофу, т. к. n – 1 = 2 (например, для узлов а и б).

2. Составляем уравнения по певому и второму законам Кирхгофа

Для узла "а" - I₁ - I₂ + I₄ = 0.

Для узла "б" - I₁ + I₂ - I₃ - I₅ = 0.

Остальные m - (n - 1) = 3 уравнения составляем по второму закону Кирхгофа.

Для контура I - R₁·I₁ - R₂·I₂ = - E₁ + E₂.

Для контура II - R₂·I₂ + R₃·I₃ + R₄·I₄ = - E₂ - E₃.

Для контура III - - R₃·I₃ + R₅·I₅ = E₃.

Решив систему, состоящую из пяти уравнений, находим пять неизвестных токов. Если какие-либо значения токов оказались отрицательными, то это означает, что действительные направления этих токов противоположны первоначально выбранным.

При расчётах сложных цепей с использованием ЭВМ удобна матричная форма записи. Уравнения, составленные по законам Кирхгофа, запишем в виде

- I₁ - I₂ + 0 + I₄ + 0 = 0

I₁ + I₂ - I₃ + 0 - I₅ = 0

R₁·I₁ - R₂·I₂ + 0 + 0 + 0 = - E₁ + E₂

0 + R₂·I₂ + R₃·I₃ + R₄·I₄ + 0 = - E₂ - E₃

0 + 0 + - R₃·I₃ + 0 + R₅·I₅ = E₃.

В матричной форме

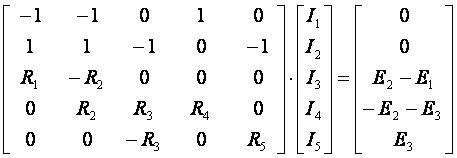
или [R]·[I] = [Е],

где [R] – квадратная (5 х 5) матрица, элементами которой являются коэффициенты при неизвестных токах в исходных уравнениях;

[I] – матрица - столбец неизвестных токов;

[E] – матрица - столбец, элементами которой могут быть алгебраическая сумма ЭДС.

Решение матричного уравнения ищут в виде

[I] = [R]^-1·[E],

где [R]^-1 – матрица, обратная матрице [R].

Рассмотренный метод расчета неудобен, если в цепи имеется большое количество узлов и контуров, поскольку потребуется решать громоздкую систему уравнений. В таких случаях рекомендуется применять метод контурных токов, позволяющий значительно сократить число расчетных уравнений 2.

Метод контурных токов

Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.

Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).

Э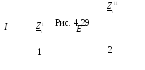та схема эквивалентна, если

а)E = IZ_i^I;

б) Z_i^II = Z_i^I.

1) Топологический анализ схемы.

а) Как и в предыдущем методе, определяют число ветвей b.

б) Определяют число узлов у.

в) Подсчитывают число независимых контуров N_k = b – y + 1.

Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.

Все контуры нумеруют и каждому контуру присваивают свой контурный ток: I_k1; I_k2;I_kNk.

За положительное направление контурного тока принимают положительное направление обхода контура.

2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений N_k = N_kпорядка:

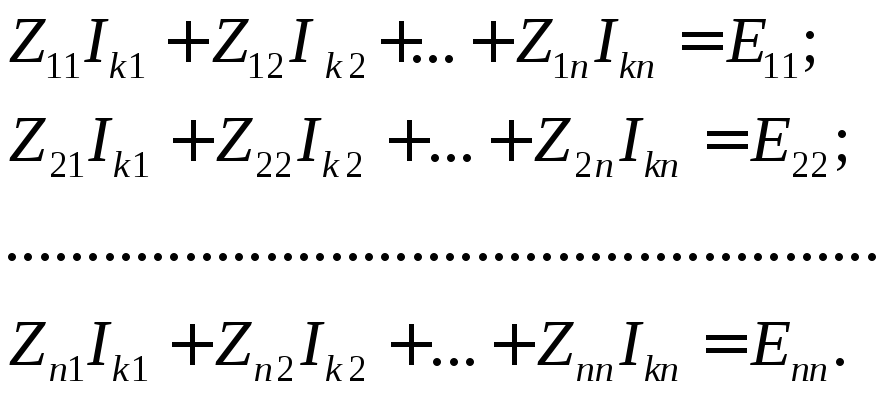
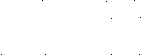
где I_ki– контурный токi-го контура;

Z_ii– собственное сопротивлениеi-го контура и равно алгебраической сумме сопротивлений, входящих вi-й контур;

Z_ji– сопротивление смежных ветвей междуi-м иj-м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;

E_ki– контурная ЭДСi-ого контура. Она равна алгебраической сумме ЭДС, входящих вi-й контур. Контурная ЭДСE_kiберется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.

3) По правилу Крамера находят контурные токиI_ki=.

4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. В алгебраической сумме контурные токи берутся со знаком «+» , если ток ветви и совпадает с контурным током и «–» если не совпадает.

Если токи ветви оказались положительными, то выбранное направление тока совпадает с истинным и наоборот.

Пример.Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.

1. Проводим топологический анализ

а) b= 6; б)y= 4;в)N_k= 6 – 4 + 1=3.

2) Составим систему уравнений по методу МКТ

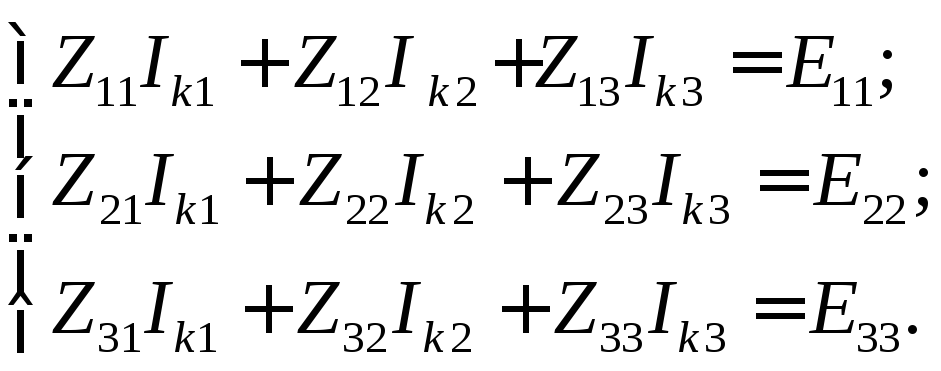
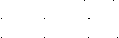
г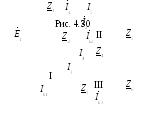де:

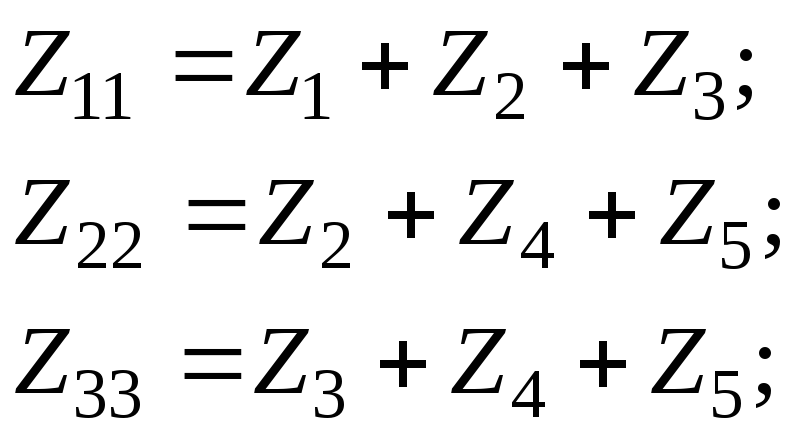
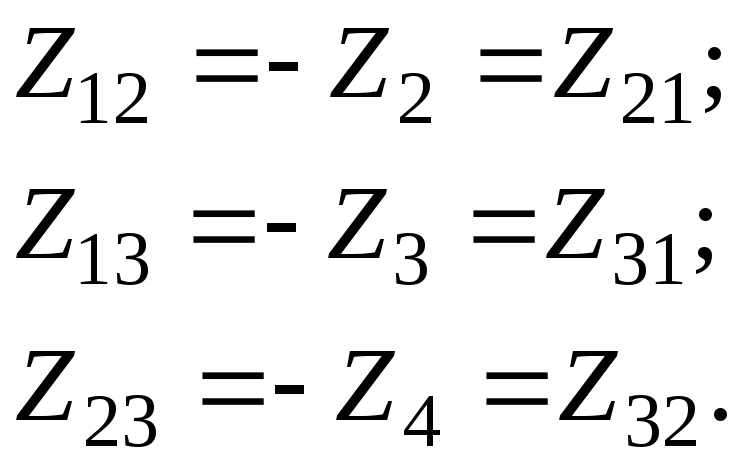
E₁₁= E₁; E₂₂ = 0;E₃₃ = 0.

3) По методу Крамера находим контурные токи I_ki = .

4) Находим токи в ветвях: I₁ = I_k1; I₂ = = I_k1 – I_k2; I₃ = I_k1 – I_k3; I₄ = –I_k2 + I_k3; I₅ = I_k2; I₆ = I_k3.

Пример 2. Рассмотрим электрической цепи постоянного тока, рис. 2.21.

1. Проводим топологический анализ

а) b= 5; б)y= 3;в)N_k= 5 – 3 + 1=3.

2) Для каждого контура записывают уравнение второго закона Кирхгофа,

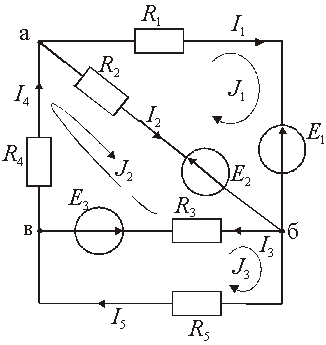Рис. 2.21. – Расчетная схема для метода контурных токов

В каждом из трех контуров протекает свой контурный ток J₁, J₂, J₃. Произвольно выбираем направление этих токов, например, по часовой стрелке. Составляем уравнения по второму закону Кирхгофа для каждого контура с учетом соседних контурных токов, протекающих по смежным ветвям

(R₁ + R₂)·J₁ - R₂·J₂ = E₂ - E₁

- R₂·J₁ + (R₂ + R₃ + R₄)·J₂ - R₃·J₃ = - E₂ - E₃

- R₃·J₂ + (R₃ + R₅)·J₃ = E₃.

Решив систему уравнений, находят контурные токи J₁, J₂, J₃. Затем определяют реальные токи в ветвях, причем токи во внешних ветвях равны контурным, а в смежных – алгебраической сумме 2-х контурных токов, протекающих в данной ветви

I₁ = J₁; I₂ = J₂ - J₁; I₃ = J₂ - J₃; I₄ = J₂; I₅ = J₃.

Исходная система уравнений в матричной форме

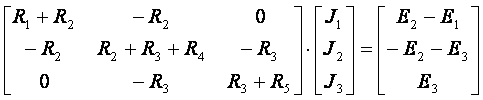
или

[R]·[J] = [E],

где [R] – квадратная матрица коэффициентов контурных токов;

[J] – матрица – столбец контурных токов; [E] – матрица – столбец ЭДС.

Решением матричного уравнения является матрица

[J] = [R]^-1 ·[E],

где [R]^-1 – матрица, обратная матрице [R]

• Пример 3. Для электрической цепи, схема которой приведена на рис. 1.1, получим следующие уравнения:

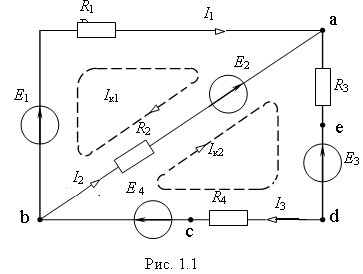
получим следующие уравнения:

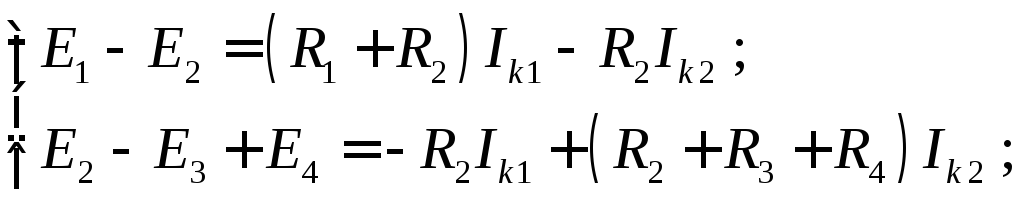
По методу Крамера найдем контурные токи:

Действительные токи в ветвях: I1 = Ik1; I2 = Ik2 – Ik1; I3 = Ik2.

Пример 4. Расчет цепи методом контурных токов на рис. 2.22.

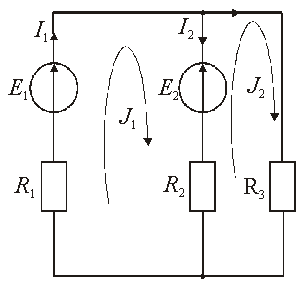Рис. 2.22. – Расчет цепи методом контурных токов

Для схемы замещения электрической цепи, показанной на рис. 2.22, задано: E₁ = 30 B; E₂ = 10 В; R₁ = 8 Ом; R₂ = 15 Ом; R₃ = 36 Ом. Требуется определить токи в ветвях методом контурных токов. Составить баланс мощности.

Схема содержит три ветви (m = 3), два узла (n = 2). Выбираем положительные направления токов в ветвях произвольно. Число уравнений, составленных по методу контурных токов, равно m - (n - 1) = 2. Задаем направление контурных токов (например, по часовой стрелке) и составляем систему уравнений

(R₁ + R₂)·J₁ - R₂·J₂ = E₁ - E₂

- R₂·J₁ + (R₂ + R₃)·J₂ = E₂.

Подставляя численные значения сопротивлений резисторов и ЭДС в приведённые уравнения, находим контурные токи J₁, J₂ (Например, методом определителей)

20 = 23·J₁ – 15·J₂

10 = - 15·J₁ + 51·J₂

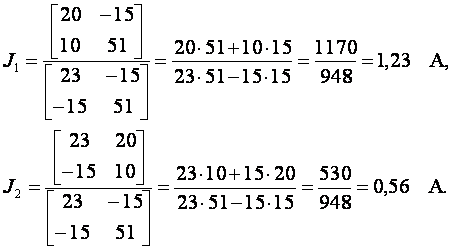
Токи в ветвях

I₁ = J₁ = 1,23 А; I₂ = - J₂ + J₁ = 1,23 - 0,56 = 0,67 А; I₃ = J₂ = 0,56 А.

Составляем баланс мощностей.

Мощность генераторов (источников)

Р_И = Е₁·I₁ - Е₂·I₂ = 30·1,23 – 10·0,67 = 30,2 Вт,

где произведение Е₂·I₂ имеет знак минус (ток через источник не совпадает с ЭДС, значит источник ЭДС работает в режиме потребителя электрической энергии).

Мощность, потребляемая нагрузкой, составляет

Р_Н = R₁·I₁² + R₂·I₂² + R₃·I₃² = 8·1,23² + 15·0,56² + 36·0,56² = 30,13 Вт.

Погрешность

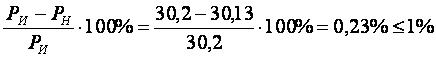
составляет менее 1%, т. е. токи найдены верно.

Метод узловых потенциалов (МУП)

Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.

Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).

а) I = E/Z_i^I;

б) Z_i^II = Z_i^I.

1) Топологический анализ.

а) Подсчитывают число ветвей bи число узловy.Определяется количество независимых узловN_y =y – 1.

б) Нумеруют все узлы. Один из узлов, к которому сходится наибольшее число ветвей, считают нулевым, где – потенциал нулевого узла.

2) По 1-му закону Кирхгофа составляют уравнения для Nузлов схемы и решают их относительно потенциалов узлов:

,

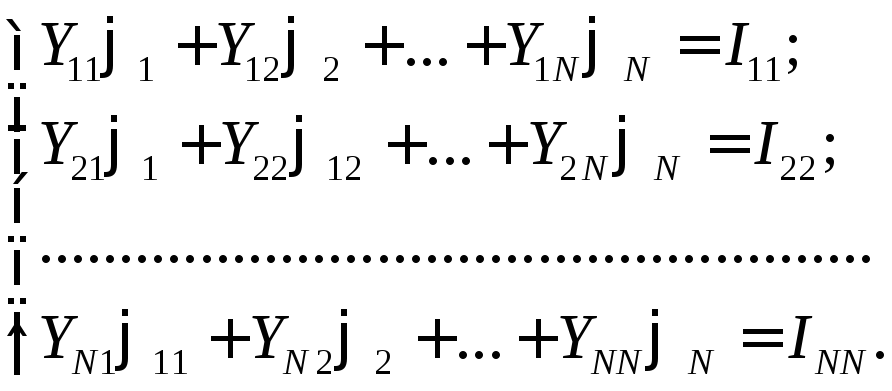
где Y_ii– собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся вi-м узле, все они берутся со знаком «+»;

Y_ij– межузловая проводимость междуi-м иj-м узлами. Проводимости всех узлов берутся со знаком «–»;

I_ii– алгебраическая сумма токов источников тока, сходящихся вi-м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».

3) Потенциалы узлов находят по формуле Крамера

.

4) Токи в ветвях находят по закону Ома

I= (₁ –₂)/Z.

Пример.Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.

П

I₂

Z₂

редварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33).

Z₁

Z₂

Z₃

Z₄

E₁

E₂

I

I₁

I₂

I₄

I

I₃

I₁

Z₁

Z₃

Z₄

Рис. 4.32 Рис. 4.33

Проведем топологический анализ.

а) число ветвей b= 4;

б) число независимых узлов N_у= 2, их потенциалы: φ₁и φ₂(рис. 4.33).

Составим систему уравнений по методу узловых потенциалов:

;

.

По методу Крамера найдем потенциалы узлов .

По закону Ома найдем токи во всех ветвях схемы:

.

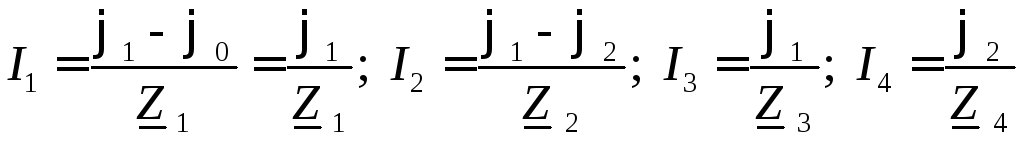
1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме цепи переменного тока