Задание 5

В среднем по 15 % договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая будет связано с выплатой страховой суммы:

а) три договора;

б) менее двух договоров.

Решение:

1) По формуле Бернулли, вероятность того, что в 10-ти договорах, в каждом из которых вероятность выплаты равна 0,15, событие наступит ровно 3 раза, равна

2) Событие А «выплата страховой суммы менее двух договоров» состоит из двух событий:

А1 — выплата страховой суммы по одному договору: k = 1

А2 — невыплата страховой суммы по договорам: k = 0

Ответ: а) P=0,13 б) P=0,544

Задание 6

Аудиторную работу по теории вероятности успешно выполнило 50% студентов. Найти вероятность того, что из 400 студентов успешно выполнят:

а) 150 студентов;

б) не менее 150 студентов;

в) от 150 до 300 студентов.

Решение:

Решение.

а) Случайная величина X — число «успешных студентов» имеет биноминальное распределение, поэтому , где — функция Гаусса

По условию задачи n=400, m=150, p=0,5, q=0,5. Поэтому (Локальная теорема Муавра — Лапласа)

б) Для вычисления Р(m150) воспользуемся интегральной теоремой Муавра-Лапласа:

Р1(150m400) = Ф₀(x₂) – Ф₀(x₁), где

Ф₀(20,0 ) – Ф₀(–5) ≈ 0,5 – (–0,5) 1

в) Находим по таблице значений функции Лапласа:

P(150≤m≤300) = Ф₀(x₂) – Ф₀(x₁), где . ПоэтомуР(150≤m≤300) = Ф₀(10) – Ф₀(–5) = 0,5 – (–0,5) 1

Задание 7

Задан закон распределения дискретной случайной величины в виде таблицы (в первой строке указаны возможные значения случайной величины, во второй – соответствующие вероятности).

Найти:

а) функцию распределения;

б) математическое ожидание;

в) дисперсию;

г) среднее квадратическое отклонение;

д) коэффициент ассиметрии.

Начертить график закона распределения и показать на нём вычисленные математическое ожидание и среднее квадратическое отклонение

xi	5	15	25	35	45
pi	0,1	0,2	0,3	0,2	0,2

Решение:

1. Функцией распределения дискретной случайной величины Х называется функция F(x), определяющая для каждого значения х вероятность того, что случайная величина Х примет значение, меньше х:

F(x)=Р(Х<х)

xi	5	15	25	35	45	x>45
F(xi)	0	0,1	0,3	0,6	0,8	0,1

2. Математическое ожидание

3. Дисперсия среднее квадратичное отклонение X:

4. коэффициент ассиметрии. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии:

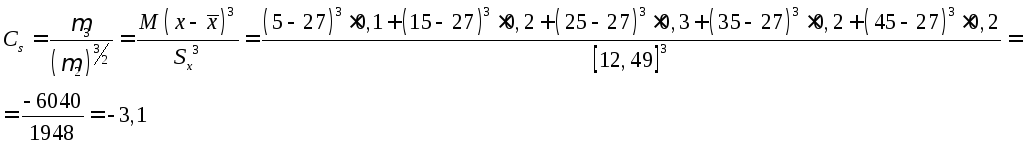
Задание 8

Для приведённых в таблице 5 выборочных данных:

а) построить вариационный и статистический ряды;

б) построить полигоны частот и накопительных частот;

в) вычислить среднюю величину, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициенты ассиметрии и эксцесса.

Исходные данные для задания 8

Номера наблюдений	Данные для задачи
	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.
Данные	3	4	5	3	4	6	8	2	3	5
Номера наблюдений	11.	12.	13.	14.	15.	16.	17.	18.	19.	20.
Данные	5	3	7	5	9	3	5	7	4	6