Оценивание параметров нелинейных моделей

Рассмотрим модель, нелинейную относительно неизвестных параметров

. (4.64)

После линеаризации переменных модель (4.64) примет вид

, , (4.65)

где , , , – линеаризованные переменные.

Запишем модель (4.65) в общем виде

, (4.66)

где – вектор неизвестных параметров; – вектор линеаризованных переменных.

В модели (4.66) переменные и значения наблюдаемы (контролируемы) и являются входами и выходами объекта идентификации.

Результаты наблюдений представим в виде

, . (4.67)

Эти функции можно разложить в ряд Тэйлора в окрестности некоторой точки , сохранив лишь члены первого порядка малости (первые производные), а именно

или перенося свободный член в левую часть, имеем

, (4.68)

где .

Вычисленные значения частных производных представим матрицей наблюдений размерности ,

.

Отклонения параметров модели представим вектором

,

размерности .

Отклонения значений функции в точке разложения соответственно вектором

,

размерности .

Тогда выражение (4.68) в матричной форме примет вид

. (4.69)

В уравнение (4.69) линейно входит неизвестный вектор .

Процедура вычисления оценок неизвестных параметров модели такова:

1. выбираются значения оценки параметров по возможности наиболее близкими к искомым значениям ;

2. далее вычисляем для известных значений и

и разности

,

где – наблюденное значение выходной переменной на -ом наблюдении;

3. с учетом введенных обозначений результаты вычислений запишем в виде уравнения , решая которое, получим ; (4.70)

4) вектор отклонения параметров дает возможность вычисления уточненных значений

5) новые значения принимаются за базовые

и осуществляется переход к п.2.

В качестве меры эффективности процедуры выбирают квадрат невязки

(4.71)

Процедура уточнения параметров повторяется до тех пор, пока изменения параметров не станут крайне малыми.

Функция (4.71) многоэкстремальна, а потому существуют различные наборы удовлетворяющие (4.71).

Важное место занимает определение начальных параметров (см. п.1) процедуры. Зачастую используют для этого графические, аналитические или интуитивные методы.

Если для разных начальных значений процедура сходится к разным b, то нужно внимательно анализировать полученные результаты.

Процесс может сходиться к истинному значению, а может и расходиться.

На практике плохая сходимость может быть обусловлена удаленностью первоначального выбора параметров от истинного, высокой корреляцией некоторых параметров, когда матрица нормальных уравнений почти вырожденная, либо структурной неадекватностью объекта.

Если относительно найденных оценок параметров можно разложить функции в ряд Тейлора, и она будет линейна в пределах нескольких средних квадратичных отклонений, то можно провести обычный линейный статистический анализ, как и в МРА, а именно построить доверительные интервалы на параметры b и функцию [17].

Поскольку процесс уточнения оценок параметров итерационный, то процедуру МНК-оценивания (4.70) по всем наблюдениям можно заменить на рекуррентную, обеспечивающую уточнение оценок параметров модели для вновь поступивших с объекта наблюдений , .

При этом можно воспользоваться оптимальным одношаговым алгоритмом (4.53), не требующим вычисления ковариационной матрицы, т.е. обращения матрицы .

Рекуррентная процедура вычисления оценок после очередного -го наблюдения на объекте входных переменных и выходной переменной выглядит следующим образом:

1. вычисление невязки между наблюденным и предсказанным значением выходной переменной (4.72)

2. вычисление значений вектора частных производных для наблюденного (4.73)

3. вычисление оценок

4. и переход к п.1.

Эффективность поиска истинных значений коэффициентов модели объекта, как и в МНК-процедуре, существенно зависит от выбора начальных оценок , уровня помех .

Структурная схема, отображающая процедуру идентификации, приведена на рис. 4.3. Векторные величины представлены двойными линиями, скаляры – простыми линиями. Ненаблюдаемая часть объекта выделена штрих-пунктирной линией.

В момент расчета используется предыдущая оценка . На схеме показан итог работы идентификатора оценка , которая будет использована на следующем шаге.

Модель

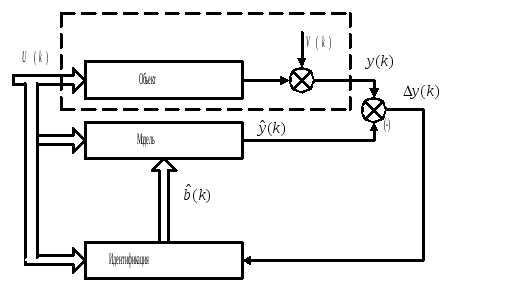
Рис. 4.3. Структурная схема идентификации рекуррентными методами