u-lectures сопромат

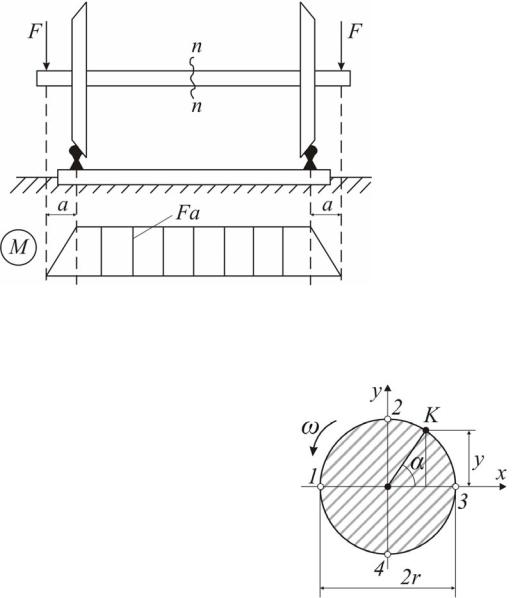
351

Рис. 12.3

При равномерном вращении угол α = ωt , где ω – угловая скорость вращения оси. Следовательно,

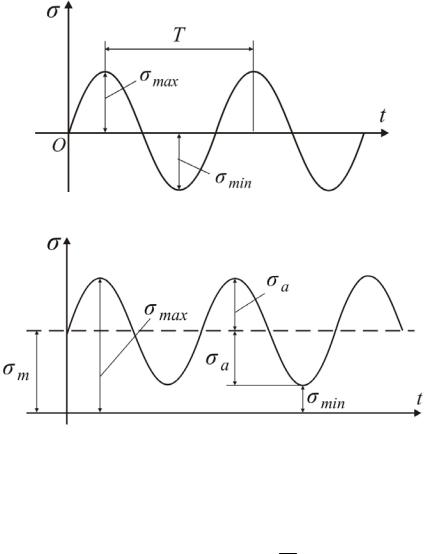
По уравнению (12.1) построен график, изображенный на рис. 12.5. Напряжения изменяются во времени периодически: через определенный промежуток времени Т (период) они проходят одно и то же значение, причем характер изменения напряжений в начальной и конечной точках периода одинаков.

Изменение напряжений за один период называется циклом напряжений. В приведенном примере и на рис. 12.5 рассмотрен так называемый симметричный цикл. У симметричного цикла σ max и σ min равны между собой, но про-

тивоположны по знаку.

352

Рис. 12.5

Рис. 12.6

Если к вращающемуся валу приложить дополнительную продольную растягивающую силу постоянной величины, то к напряжениям (12.1) добавится

среднее постоянное напряжение цикла σm = NA . Тогда напряжение в точке

будет меняться, например по закону, изображенному на рис. 12.6. Такой цикл носит название асимметричного (σmax ≠ σmin ).

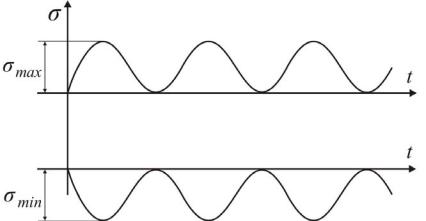
Если знаки σmax и σmin одинаковы, цикл называется знакопостоянным, если различны – знакопеременным. В том случае, если значение σmax или σmin

равно нулю, цикл называется пульсирующим, или отнулевым (рис. 12.7). Любой цикл характеризуется двумя параметрами:

(наибольшее значение переменной составляющей цикла напряжений).

353

Рис. 12.7

Отношение σmin к σmax называется коэффициентом асимметрии цикла:

Для пульсирующего цикла R = 0, а для симметричного R = −1.

Циклы, имеющие одинаковое значение коэффициента R , называются подоб-

ными.

Размахом напряжений называют разность

Основной характеристикой выносливости материала является кривая усталости, получаемая экспериментальным путем. По кривой усталости определяется значение предела выносливости – характеристики механических свойств материалов, позволяющей количественно оценить сопротивление усталости образца. Максимальное по абсолютному значению напряжение цикла, которое не вызывает разрушения образца при неограниченно большом числе цик-

лов, называется пределом выносливости σR . При симметричном цикле σR ,

имеет наименьшее значение и обозначается σ−1 .

Для опытного определения величины σ−1 используются специальные маши-

ны, в которых вращающийся образец круглого сечения подвергается чистому изгибу. Из испытываемого материала изготавливают не менее десяти одинаковых образцов. Задавшись различными значениями напряжения σmax , опре-

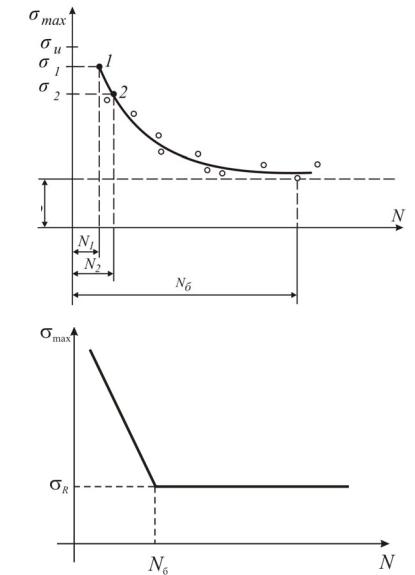
деляют число N циклов, необходимых для каждого образца до разрушения. По результатам испытания строят кривую усталости (кривую Веллера) или кривую выносливости (σmax − N ), см. рис. 12.8. Она имеет горизонтальную

асимптоту, ордината которой равна пределу выносливости σ−1 . Кривые ус-

талости также могут строиться в логарифмических lgσ − lg N и полулога-

354

рифмических lgσ − lN , σ − lg N координатах, где σ – напряжение σmax , σmin или σa ; N – число циклов до разрушения.

σNR

а

б

Рис. 12.8

Опыты показали, что если стальной образец не разрушается при числе циклов, равном N =107 , то он не разрушается и при большем их числе. Поэтому

испытание образцов прекращается при N =107 . Это число циклов называется

базой испытания.

Кривые выносливости для цветных металлов не имеют горизонтальных асим-

птот. Поэтому для них база испытания увеличивается до N =108 циклов и устанавливается предел ограниченной выносливости. Чтобы иметь представление о порядке величин числа циклов заметим, что вагонная ось на пути от

Москвы до Владивостока испытывает около 3 106 циклов.

355

Основной тип кривой усталости – кривая с четко выраженным горизонтальным участком (рис. 12.8, б). При этом выявляется физический предел усталости (выносливости). Кривые такого типа характерны для черных металлов и титана. Кривые усталости с асимптотическим приближением правой ветви к горизонтали (рис. 12.8, а) характерны для цветных металлов, а также для черных металлов (в случае влияния коррозионной среды). При этом выявляется условный предел выносливости σNR для определенной базы испытания.

Испытания на выносливость при растяжении, сжатии и кручении требуют более сложного оборудования и поэтому проводятся редко. Соответствующие пределы выносливости определяют по известному пределу выносливости при изгибе в условиях симметричного цикла нагружения по эмпирическим соотношениям:

Факторы, влияющие на усталостную прочность материала

Концентрация напряжений

Явление повышения напряжений по сравнению с номинальными т.е. вычисленными по обычным формулам, называется концентрацией напряжений, а их причина, – концентратором напряжений. К концентраторам напряжений относится резкое изменение размеров сечений детали (выточки, надрезы, отверстия, шпоночные пазы, и др.). Зона распространения повышенных напря-

жений носит локальный характер, т.е.

ограничивается небольшой областью, непосредственно прилегающей к очагу концентрации.

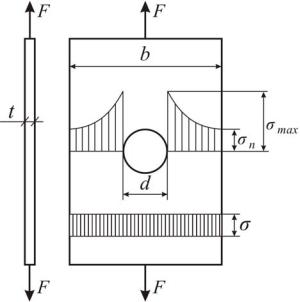
Например, при растяжении полосы с отверстием (рис. 12.9) закон равномерного распределения напряжений вблизи отверстий нарушается. У края отверстия появляется пик напряжений. Основным показателем повышения напряжения в непосредственной близости к концентраторам напряжений служит теоретический коэффициент концентрации напряжений, который равен отношению максимального нормального напряжения в зоне концентрации к номинальному:

356

Однако при действии переменных напряжений различные материалы поразному реагируют на наличие одного и того же концентратора, т.е. обладают различной чувствительностью к концентрации напряжений. Поэтому вводят так называемый эффективный коэффициент Kσ , Kτ концентрации напря-

жений:

где σ−1 , τ−1 – предел выносливости образца без учёта концентрации напряжений при симметричном цикле; σ−1k , τ−1k – предел выносливости образца с

учётом концентрации напряжений при изгибе и кручении соответственно. Числовое значение Kσ , Kτ можно определить по результатам усталостных

испытаний. При отсутствии экспериментальных данных можно воспользоваться формулой

Kσ =1 + qσ (ασ −1), Kτ =1 + qτ (ατ −1),

где qσ − коэффициент чувствительности металла к концентрации напряже-

ний.

Чем выше прочность стали, тем больше коэффициент чувствительности. Для высокопрочных сталей qσ 1. Для углеродистых сталей он становится рав-

ным 0,6 ÷ 0,8 q σ . Чугун малочувствителен к концентрации qσ = 0.

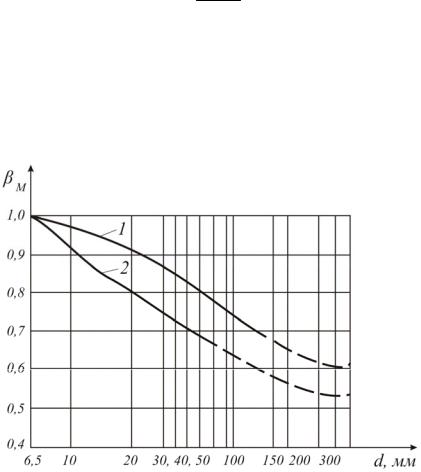
Масштабный фактор

Опытным путем установлено, что с увеличением размеров поперечных сечений предел выносливости падает. Так, например, предел выносливости образца диаметром 7 мм из стали, идущей на изготовление вагонных осей равен σ−1 = 230 МПа, а предел выносливости вагонной оси диаметром 170 мм –

σ−1 =120 МПа. Это объясняется тем, что в образцах с большим объемом ма-

териала содержится большее количество дефектов (раковины, неметаллические включения и т.п.) и локальных повреждений, что снижает предел выносливости.

Снижение предела выносливости при увеличении размеров деталей и элементов конструкций учитывается введением масштабного коэффициента

358

где σ−1п, τ−1п– предел выносливости образца с полированной поверхностью при изгибу и кручении; σ−1 , τ−1 – предел выносливости такого же образца с

заданным состоянием поверхности.

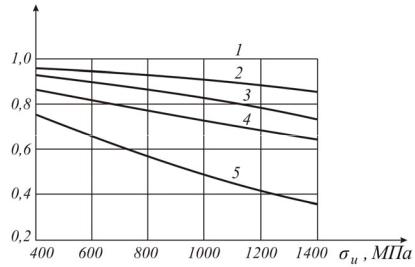
На рис. 12.11 даны значения коэффициента βп в зависимости от состояния

поверхности детали (1 – полирование; 2 – шлифование; 3 –тонкое точение; 4

– грубое точение; 5 – наличие окалины).

KFσ

Как видим, снижение предела выносливости тем больше, чем грубее поверхностная обработка детали, причем это снижение более значительно для материалов с высоким пределом прочности. Поэтому наиболее важные детали механизмов и машин подвергают специальной поверхностной обработке – поверхностному упрочнению. Усталостная прочность повышается при повышении чистоты поверхности, что достигается применением операций полирования, шлифования, цементации, обработки токами высокой частоты, обработках роликами и др. Это повышение оценивается коэффициентом

V σ−1Д

359

где σ−1Д упр и σ−1Д - пределы выносливости соответственно упрочненной и

неупрочненной детали. Чем выше уровень концентрации напряжений, тем эффект упрочнения возрастает, а увеличением размеров детали уменьшается. Методы упрочнения приводят к повышению пределов выносливости в 2-3 раза и более, вследствие чего являются мощным средством повышения надежности и долговечности машин при одновременном снижении их массы.

Еще один не маловажный фактор, влияющий на предел выносливости – анизотропия материала, учитывается коэффициентом K A , которую рассматрива-

ют, если главное напряжение σ при изгибе и растяжении-сжатии направлено перпендикулярно направлению прокатки материала. В табл. 12.1 приведены значения K A в зависимости от σв материала.

Таблица 12.1

Значения коэффициента анизотропии материала

Внешняя среда

Усталостная прочность зависит от среды, в которой эксплуатируется деталь. Коррозионная среда (вода, соленая вода, кислоты, пары) резко снижает усталостную прочность. В некоторых случаях спад предела выносливости достигает 70-80%. Применение защитных покрытий поверхности (окраска, металлизация, азотирование, цементация и др.) уменьшает эффект действия коррозионной среды.

Высокие температуры уменьшают, а низкие несколько повышают усталостную прочность. Радиационное облучение снижает предел выносливости в результате повышения хрупкости материалов.

Комплексный учет, перечисленных выше факторов, согласно (12.7)- (12.12) оценивается коэффициентом снижения предела выносливости при растяжении сжатии

360

при кручении

Таким образом, предел выносливости детали с учетом выше перечисленных факторов определяется

Значения σ−1Д обычно в 2-6 (и более) раз меньше, чем характеризующее только свойства материала значение предела выносливости σ−1 гладких лабораторных образцов.

Тема 12.2 Коэффициент запаса при циклическом нагружении и методы его определения

Для расчета элементов машин и сооружений необходимо располагать данными о пределе выносливости при различных циклах. Поэтому проводят испытания и при асимметричных циклах. По результатам испытаний строят диаграмму предельных напряжений (диаграмму Хея), характеризующую зависимость между величиной среднего напряжения σm и амплитудного значения

σa предельного цикла. Каждая пара напряжений ( σm −σa ), определяющая

предельный цикл, изображается некоторой точкой на диаграмме (рис. 12.12). Все эти точки в общем случае располагаются на кривой АСВ, которая на оси ординат отсекает отрезок, равный пределу выносливости симметричного цикла σ−1 (при этом цикле σm = 0 ), а на оси абсцисс – отрезок, равный вре-

менному сопротивлению σв . В этом случае действуют напряжения постоянные во времени,

σmax = σmin = σв = σ+1.

Точка С (с координатами σm = σa = σ0 2 ) соответствует пределу выносливости σ0 при отнулевом цикле.

Рассмотрим вопрос об использовании построенной диаграммы. Пусть заданному циклу соответствует точка N (с координатами σ m и σ a ). Очевидно, что

любая другая точка, лежащая на том же луче, соответствует циклу, подобному данному. Все циклы, изображаемые точками отрезка ОМ, безопасны в отношении усталостного разрушения. При этом цикл, изображаемый точкой М