лекция 2_конспект

Лекция 2 Орбитальное движение космических аппаратов

Любой объект, находящийся в космическом пространстве, движется. Траектории движения космических аппаратов определяются, в первую очередь, целевыми задачами,

решаемыми этими аппаратами. Замкнутые траектории движения называются орбитами.

Космические аппараты информационного обеспечения работают на всех известных типах замкнутых околоземных орбит: КА связи – на низких круговых, высокоэллиптических и геостационарной орбитах, КА навигации и времени – на средних круговых и высокоэллиптических, геостационарной и круговых геосинхронных наклонных орбитах, КА геодезии и дистанционного зондирования Земли – на низких круговых и, в частности, на солнечно-синхронных орбитах. Для успешного создания и эксплуатации космического аппарата необходимо иметь представление о принципах орбитального движения, возмущающих силах,

действующих на космический аппарат на орбите, прогнозировать движение космического аппарата в околоземном пространстве, выбирать орбиты с учётом эффективного

использования солнечных батарей, а также планировать сеансы связи спутников с НКУ.

СПИСОК СОКРАЩЕНИЙ И УСЛОВНЫХ ОБОЗНАЧЕНИЙ

1

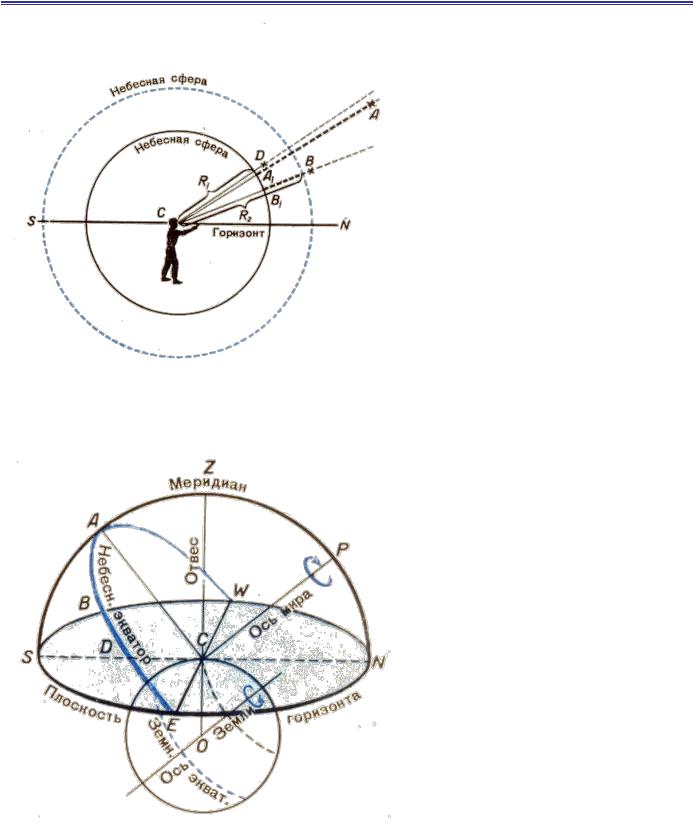
Небесная механика.

Проецирование космических объектов на небесную сферу

Небесной сферой называется воображаемая поверхность произвольного радиуса, на которую наблюдатель проецирует положение космических объектов.

Небесная сфера является удобной

космических объектов, поскольку координаты космических объектов описываются только тремя углами в сферической системе координат.

Находясь на поверхности Земли, наблюдатель строит небесную полусферу с центром в точке наблюдения, при этом линия небесного экватора оказывается параллельной земному экватору, а ось мира – параллельной оси вращения Земли, а плоскость горизонта – перпендикулярной радиусу Земли.

Построенная таким образом небесная полусфера имеет большую погрешность определения характера движения космических аппаратов, поскольку КА движутся в инерциальном пространстве вокруг центра Земли, а не вокруг наблюдателя. Поэтому необходимо приведение наблюдаемой небесной сферы к центру Земли.

2

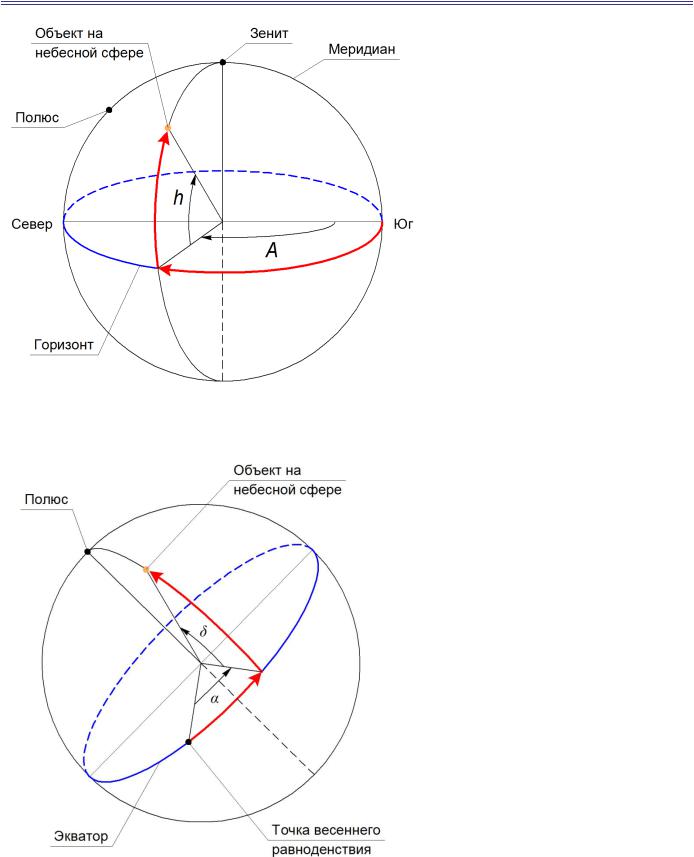
Небесная механика

Геоцентрические системы координат

а) горизонтальная

h – угловая высота,

A – азимут

Горизонтальная геоцентрическая система координат удобна тем, что координаты небесных объектов можно определять непосредственным их наблюдением. Однако в горизонтальной системе координат невозможно провести наблюдение и определить координаты загоризонтных объектов, поэтому горизонтальная система координат имеет региональный масштаб применения.

б) экваториальная

– прямое восхождение,

– склонение

Экваториальная система координат универсальна и потому используется для взаимной увязки объектов по всей небесной сфере. Однако определение координат небесных объектов в этой системе требует специализированного оборудования.

3

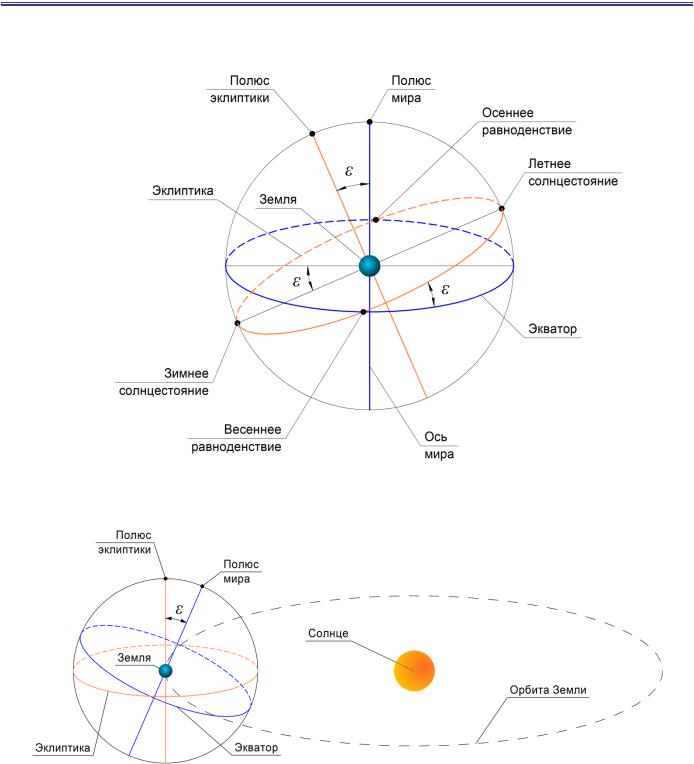
Небесная механика

Эклиптика

Эклиптика – окружность на небесной сфере, по которой в течении года перемещается центр Солнца.

– угол наклона плоскости эклиптики к плоскости экватора, = 23,45°

Вследствие наклона оси вращения Земли к плоскости орбиты, по которой Земля движется вокруг Солнца, эклиптика на небесной сфере наклонена к небесному экватору на угол 23,45°. Это приводит к тому, что освещённость КА зависит не только от положения КА на орбите, но и от текущего времени года.

4

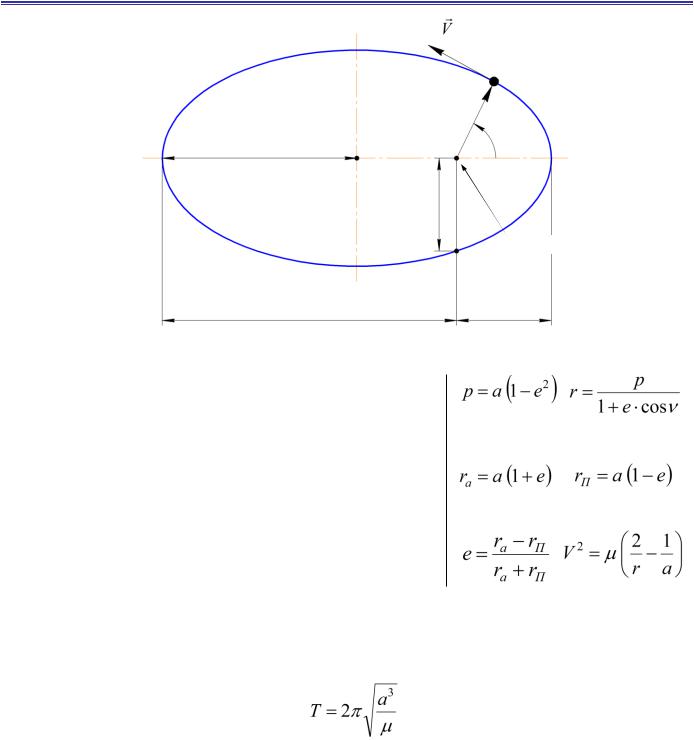
Элементы орбиты КА

КА

r

ν

а

p

Центр Земли

a – большая полуось; е – эксцентриситет;

– истинная аномалия; р – фокальный параметр ( = ±90º);

r – текущее значение величины радиус-вектора орбиты; rП – значение радиус-вектора перигея ( = 0º);

rа – значение радиус-вектора апогея ( = 180º);

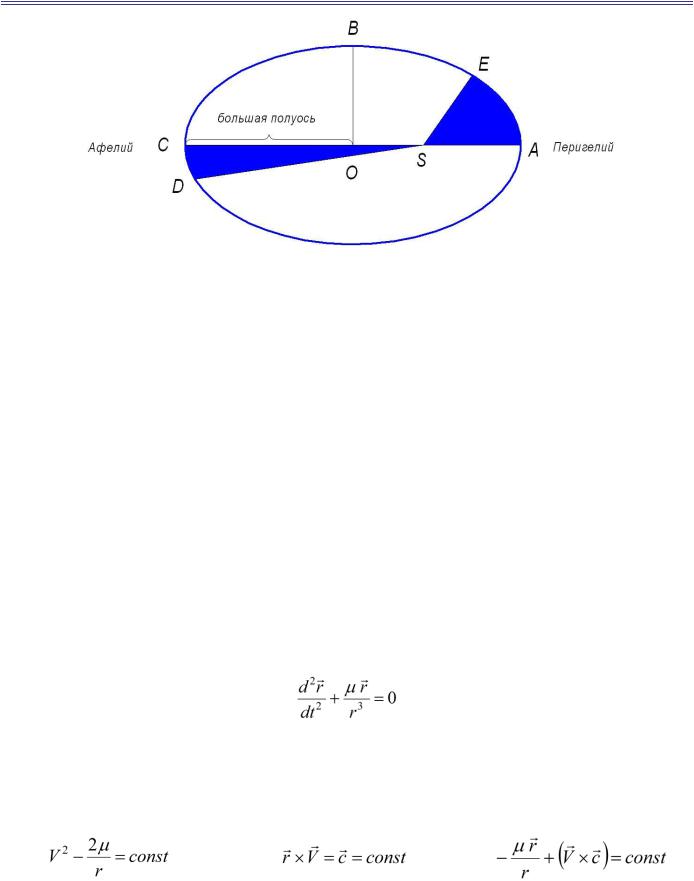
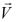– вектор скорости движения КА по эллиптической орбите;

Период обращения КА по орбите не зависит от формы орбиты:

,

следовательно:

1.Можно подобрать множество орбит с одинаковым периодом обращения

2.Периодом обращения КА можно управлять, меняя только большую полуось орбиты – это свойство используется при переводе спутника с одной точки геостационарной орбиты в другую точку

5

Положение орбиты КА в пространстве

XЭYЭZЭ – экваториальная геоцентрическая система координат

XО.ЗYО.ЗZО.З – орбитально-земная система координат

Положение плоскости орбиты КА определяют два элемента:

i – наклонение орбиты – угол между плоскостью орбиты и плоскостью экватора;

Ω – долгота восходящего узла – угол в плоскости экватора между восходящим узлом орбиты и восходящим узлом эклиптики (точкой весны).

Для того, чтобы окончательно определить положение орбиты в пространстве, вводится параметр ω – аргумент перигея – угол между линией узлов (точка весны – точка осени) и направлением из центра Земли на перигей орбиты. Этот параметр характеризует размещение апогея и перигея эллиптической орбиты относительно северного и южного полушарий Земли. В частности, для наиболее экономичного (по топливу) выведения КА на геостационарную орбиту аргумент перигея переходной эллиптической орбиты должен быть равен 0° или 180°.

Таким образом, положение орбиты КА описывается системой из пяти элементов орбиты:

a, e, i, Ω, ω

а положение КА на орбите – одним параметром: или u (аргумент широты), u = ω+

6

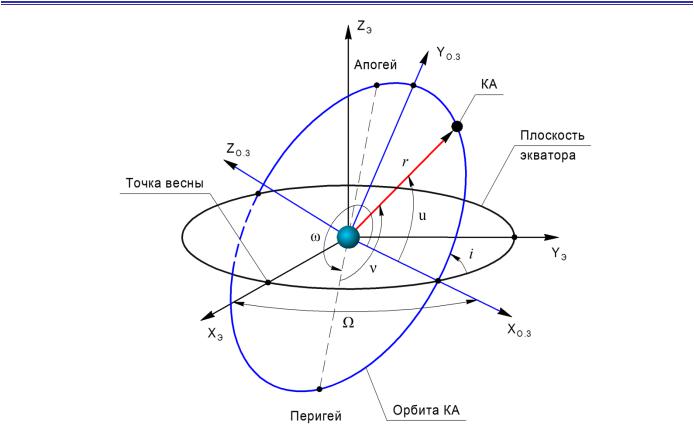
Законы Кеплера Невозмущённое движение КА

I.Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

II.Радиус-вектор планеты за равные промежутки времени описывает равные площади.

III. Квадраты периодов обращения планет относятся как кубы полуосей их

Первый закон постулирует замкнутость всех орбит в центральном поле тяготения и описывает их форму.

Второй закон позволяет вычислить линейную скорость КА на различных участках орбиты.

Третий закон определяет семейство орбит с одинаковыми периодами обращения, а также используется при расчётах траекторий перелёта между орбитами или между точками на геостационарной орбите.

Невозмущённое движение КА описывается дифференциальным уравнением:

,

где μ – гравитационный параметр; 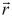– радиус-вектор обриты КА.

Закономерность невозмущённого движения определяют первые интегралы этого уравнения:

7

Возмущённое движение КА вокруг Земли

Возмущающие силы, действующие на КА

иСолнца

Основное влияние на движение космических аппаратов оказывает центральное гравитационное поле Земли

Расчет траектории движения КА вокруг Земли проводят с использованием

следующих моделей:

1)Движение в центральном гравитационном поле Земли (невозмущенное движение)

2)Движение в нецентральном гравитационном поле Земли и с учетом воздействия гравитационного поля Луны и Солнца, а также сил негравитационной природы

(возмущенное движение)

3)Движение под воздействием управляемых реактивных сил (орбитальные маневры в целях коррекции параметров орбиты)

Модели, используемые при расчёте траектории движения КА вокруг Земли, иллюстрируют эволюцию понимания реальной формы орбит КА. В начале космической эры, не обладая экспериментальными знаниями о реальных условиях космоса, использовали идеальную модель, исключающую любые возмущающие силы. При накоплении информации возмущающие силы стали учитываться, а после – использоваться для управления движением космического аппарата. В настоящее время в качестве управляющих используются комбинации из реактивных сил и возмущающих сил, характерных для орбиты функционирования КА: для низких орбит характерными являются аэродинамические силы, для высоких круговых – силы радиационного давления, и т.д.

8

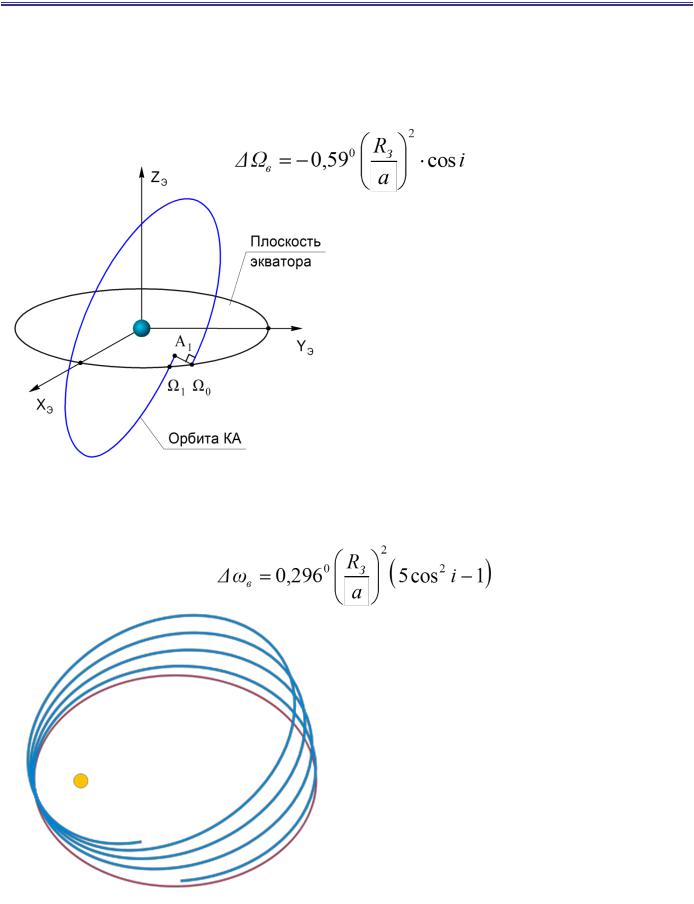
Влияние на движение КА возмущающих сил аэродинамического торможения

Сила аэродинамического торможения вызывается атмосферой Земли, которая, хоть и достаточно разрежена на высотах больше 500 км, на длительном интервале может оказывать существенное влияние на орбиту КА.

Сила сопротивления воздуха противоположна по направлению скорости движения КА и пропорциональна его миделевому сечению:

,

где сх – коэффициент сопротивления воздуха, для высот больше 500 км не зависит от формы КА и равен 2,3;

Sm – площадь миделевого сечения КА, т.е. площадь проекции спутника на плоскость,

перпендикулярную вектору скорости КА. Для неориентированного положения спутника Sm

принимается равной 1/4 площади поверхности КА;

ρа – плотность атмосферы на высоте полёта КА.

Аэродинамическое торможение учитывается в следующих случаях:

−для оценки требуемых затрат характеристической скорости на поддержание рабочей орбиты в течение срока активного существования КА;

−при определении диапазона рабочих орбит КА (определение допустимой деградации орбиты);

−при расчётах погрешностей прогнозирования положения КА.

Влияние атмосферы на время баллистического существования КА определяется из следующего соотношения:

,

где K – коэффициент, зависящий от формы орбиты и параметров атмосферы;

Сб – баллистический коэффициент, зависящий от площади миделя и массы КА.

10