ГОСЫ / вопрос 13 / Лекция 16-17

Лек ция 16

Площадь многоугольника в евклидовой геометрии. Теоремы существования измерения площади фигуры.

Теорема единственности.

Определение 16.1. Ломаной называется фигура, состоящая n-1 отрезков - звеньев ломаной.

Определение 16.2. Ломаная называется простой, если смежные звенья (А₁А₂ и А₂А₃, А₃А₄ и А₄А₅) не лежат на одной прямой и несмежные звенья не имеют общих точек.

Определение 16.3. Ломаная называется замкнутой, если ее концы совпадают (.

Определение 16.4. Объединение замкнутой ломаной и её внутренней области называется многоугольником. Замкнутая ломаная, ограничивающая многоугольник, является его границей.

Определение 16.5. Многоугольник называется ориентированным, если указан порядок обхода его вершин, т.е. .

Пусть . Введем на многоугольниках ориентации так, чтобы общие вершины и , и следовали друг за другом в одном и том же порядке. В этом случае говорят, что ориентации этих многоугольников согласованы и .

Пусть - евклидова плоскость, М - множество всех многоугольников данной плоскости, - единичный вектор, перпендикулярный плоскости ,

и - произвольные векторы, параллельные плоскости .

Смешанное произведение обозначим .

Выберем на плоскости ортонормированный базис так, чтобы .

Если в данном базисе

Пусть ориентированный n-угольник, а точка О - произвольная точка .

Определение 16.6. Число , где и называется характеристикой многоугольника F.

Если в прямоугольной системе координат плоскости вершины многоугольника имеют координаты где i= 1,2…n, то характеристику многоугольника можно записать в виде:

()

Свойства характеристики многоугольника

1). Характеристика многоугольника не зависит от выбора точки О на плоскости ;

2). Если , то > и >;

3). Если – произвольный многоугольник, то , поэтому >0 ;

4). При замене ориентации многоугольника характеристика меняет знак на противоположный, но абсолютная величина характеристики не меняется.

5). Любой многоугольник можно ориентировать так, чтобы его характеристика была положительной.

Рассмотрим множество М всех многоугольников на евклидовой плоскости. Говорят, что установлено измерение площадей многоугольников если определено отображение: , удовлетворяет следующим аксиомам:

1). Если ,то ;

2). Если F=F₁+F_2, то S(F)=S(F₁)+S(F₂);

3). Если S(P₀)=1. где Р₀ – квадрат, построенный на единичном отрезке как на стороне.

Определение 16.7. Положительное число S(F) называется мерой или площадью многоугольника F, а квадрат P₀- единичный квадрат.

Теорема 16.8. (теорема существования) Отображение по закону удовлетворяет аксиомам 1, 2, 3 измерения площадей.

Доказательство:

1. Докажем, что если F=F’, то S(F)= S(F’) .

Так как F=F’, то существует движение, которое многоугольник переводит в многоугольник . Данное движение может быть заданно двумя ортонормированными реперами и . Если - вершины многоугольника в репере , то - вершины многоугольника в репере . Поэтому по формуле () получаем , а значит, S(F)= S(F’).

2) Докажем что если F=F₁+F₂ , то S(F)= S(F₁)+ S(F₂) многоугольник.

Многоугольник F ориентирован так, чтобы >0. Введем на F₁ и F₂ ориентации, согласованные с ориентацией многоугольника . Тогда . Докажем, что .

Пусть М₀……М_к – ломаная, которая разбивает многоугольник F на многоугольники F₁ и F₂, а - радиус–векторы вершин этой ломаной, радиус-векторы вершин многоугольника А_1….А_n.

Сложив эти равенства и учитывая второе свойство характеристики, имеем

Так как точка М₀ - точка отрезка А₁А_n, то , поэтому .

Аналогично . Значит, = S(F)= S(F₁)+ S(F₂)

3) Пусть - квадрат, построенный на единичном отрезке. В системе координат его вершины имеют координаты О(0,0), А₁(1,0), А₂(0,1), А₃(1,1). Высчитав характеристику, имеем: .

Для её доказательства теоремы единственности необходимо следующие теоремы.

Теорема 16.9. Если - отображение, удовлетворяющее аксиомам 1,2,3, то , где - прямоугольник, стороны которые равны и .

Теорема 16.10. Если - отображение, удовлетворяющее аксиомам 1,2,3, то , где Р- треугольник, - одна из его сторон, а - соответствующая высота.

Теорема 16.11. (теорема единственности площади)

Если выбран единичный отрезок, то существует не более одного отображения удовлетворяющего аксиомам 1,2,3.

Доказательство: (методом от противного).

1). Пусть существуют два отображения и которые удовлетворяют аксиомам 1,2,3, при одном и том же выборе единичного отрезка.

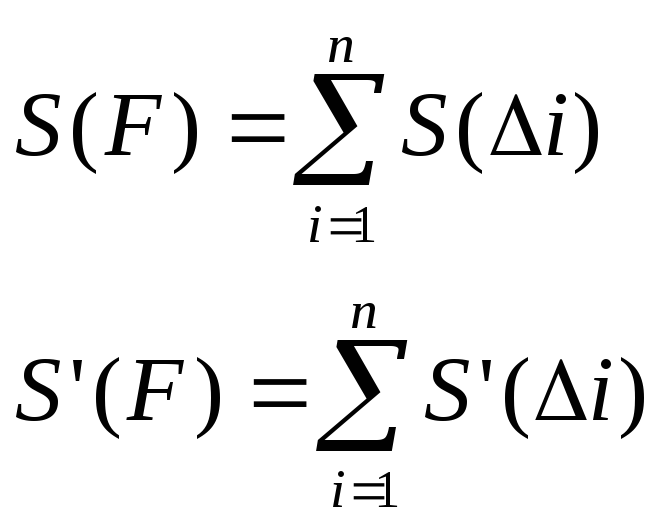
2). Возьмем произвольный многоугольник F и разложим его на конечное множество треугольников: . По аксиоме 2 имеем: при . Полученное равенство справедливо для любого многоугольника, следовательно, допущение неверно и , значит, отображения .

Следствие16.11.1. При любом способе разложения многоугольника на конечное множество треугольников сумма площадей этих треугольников одна и та же.

Следствие 16.11.2. Если вершины многоугольника А₁…А_n в прямоугольной системе координат заданы своими координатами, то

Определение 16.12. Два многоугольника называются равновеликими, если их площади равны.

Определение 16.13. Два многоугольника называются равносоставленными, если их можно разложить на одно и то же число равных многоугольников.

Если 2 многоугольника равносоставлены, то они и равновелики.