ГОСЫ / вопрос 3 / движение в пространстве

Виды движения

Определение преобразования

Обозначение

Изображение

Формулы преобразования

Элементы, определяющие преобразование

Неподвижные точки

Неподвижные прямые

Неподвижные плоскости

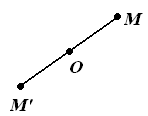
Центральная симметрия

преобразование пространства, при котором каждая точка пространства отображается на симметричную ей точку относительно центра симметрии

Z_O

Z_O(M)=M'

Если О(0,0,0):

x' = -x

y' = -y

z' = -z

центр

симметрии

центр

симметрии

всякая прямая, проходящая через центр симметрии

всякая плоскость, проходящая через центр симметрии

Если О(a,b,c):

x' = 2a - x

y' = 2b - y

z' = 2c - z

Симметрия относительно плоскости

(зеркальное отражение)

преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно данной плоскости

S_α

MO=OM'

MM' α

α=(XOY)

x' = x

y' = y

z' =-z

плоскость симметрии α

все точки плоскости

все прямые, принадлежащие плоскости α, или перпендикулярные ей

плоскость симметрии α и всякая плоскость, перпендикулярная плоскости α

α=(XOZ)

x' = x

y' =-y

z' = z

α=(YOZ)

x' =-x

y' = y

z' = z

Скользящая симметрия

преобразование пространства, представляющее собой композицию симметрии относительно плоскости α и параллельного переноса на вектор , параллельный этой плоскости

MM'

α=(XOY)

x' = x+ p₁

y' = y+ p₂

z' =-z + p₃

плоскость α

и вектор параллельного переноса

нет

всякая прямая, лежащая в плоскости α и параллельная вектору

плоскость симметрии α и всякая плоскость, перпендикулярная плоскости α и параллельная вектору

α=(XOZ)

x' = x + p₁

y' =-y + p₂

z' = z + p₃

α=(YOZ)

x' =-x+ p₁

y' = y + p₂

z' = z + p₃

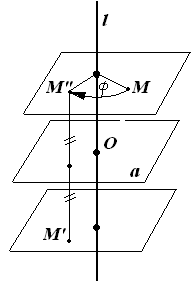
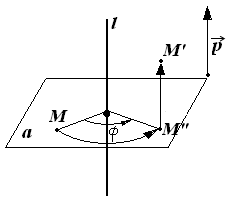
Зеркальный поворот

преобразование пространства, представляющее собой композицию поворота вокруг оси l на угол φ и симметрии относительно плоскости α, перпендикулярной этой оси

MM'

α=(XOY), a=OZ

z' =-z

плоскость симметрии α, ось поворота l и угол поворота φ

точка пересечения оси поворота l и плоскости симметрии α

ось поворота l

плоскость симметрии α

α=(XOZ), a=OY

y' =-y

α=(YOZ), a=OX

x' =-x

Виды движения

Определение преобразования

Обозначение

Изображение

Формулы преобразования

Элементы, определяющие преобразование

Неподвижные точки

Неподвижные прямые

Неподвижные плоскости

Тождественное преобразование

преобразование пространства, которое каждую точку пространства отображает на себя

Е

E(M)=M

x' = x

y' = y

z' = z

-

любая

точка

любая

прямая

любая плоскость

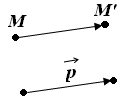
Параллельный перенос

преобразование пространства, при котором всякая точка М отображается на точку М', так что выполняется векторное равенство: , где

x' = x+ p₁

y' = y+ p₂

z' = z + p₃

вектор

нет

всякая прямая, параллельная вектору

всякая плоскость, параллельная вектору

Поворот

вокруг оси

преобразование пространства, при котором каждая точка ориентированной прямой – оси поворота l – остается неподвижной, и в любой плоскости, перпендикулярной прямой l, индуцируется (возникает) поворот этой плоскости на угол φ вокруг точки пересечения ее с прямой

l=OZ

z' = z

ось поворота l и угол

поворота φ

каждая точка оси поворота

ось поворота

всякая плоскость, перпендикулярная оси поворота

l=OY

y' = y

l=OX

x' = x

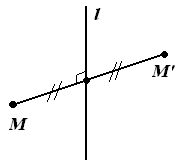
Осевая

симметрия

преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой l

(эквивалентно повороту вокруг оси l на угол, равный 180⁰)

S_l

l=OZ

z' = z

ось симметрии l

каждая точка оси симметрии

ось симметрии

всякая плоскость, перпендикулярная оси симметрии

l=OY

y' = y

l=OX

x' = x

Винтовое

движение

преобразование пространства, представляющее собой композицию поворота вокруг оси l на угол φ и переноса на вектор , параллельный этой оси

MM'

l=OZ

z' = z + p₃

ось поворота l, угол поворота φ и вектор параллельного

переноса

нет

ось поворота l

нет

l=OY

y' = y + p₂

l=OX

x' = x + p₁