Лекция № 10
Частные виды поверхностей второго порядка.
Исследование свойств поверхностей второго порядка методом сечений.
|
Название поверхности |
Определение поверхности и ее каноническое уравнение |
Изображение поверхности в системе координат |
Свойства поверхности, вытекающие из уравнения |
|
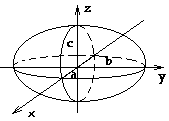
1. Эллипсоид |
Поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:
|
|
1) эллипсоид, ограниченная фигура, т.к.
2) если
3) поверхность симметричная относительно координатных осей, координатных плоскостей и центра координат. 4) центр симметрии - центр эллипсоида. 5) оси симметрии - оси эллипсоида. Каждая ось пересекает эллипсоид в двух точках, вершинах эллипсоида. Вершины эллипсоида – центры симметрии граней параллелепипеда (точки пересечения диагоналей).
|
|
2. Однополостный гиперболоид |
Поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
|
|
1) поверхность симметрична относительно координатных плоскостей, координатных осей и начала координат;
2) оси координат
– оси гиперболоида, начало координат
– центр гиперболоида, Ox
и Oy – действительные
оси, пересекают гиперболоид, каждая
в двух точках, называемых вершинами,
Ox:
3) a, b,c – в уравнении, полуоси однополостного гиперболоида. |
|
3. Двуполостный гиперболоид |
Поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
|
|
|
|
4. Эллиптический параболоид.
|
Поверхность,
которая в некоторой прямоугольной
системе координат определяется
уравнением
|
|
|
|
5. Гиперболический параболоид |
Поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
|
|
|
Исследование гиперболического параболоида методом сечений
I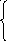 )
Пусть
)
Пусть
![]() -
плоскость сечений и
-
плоскость сечений и
![]() .
.
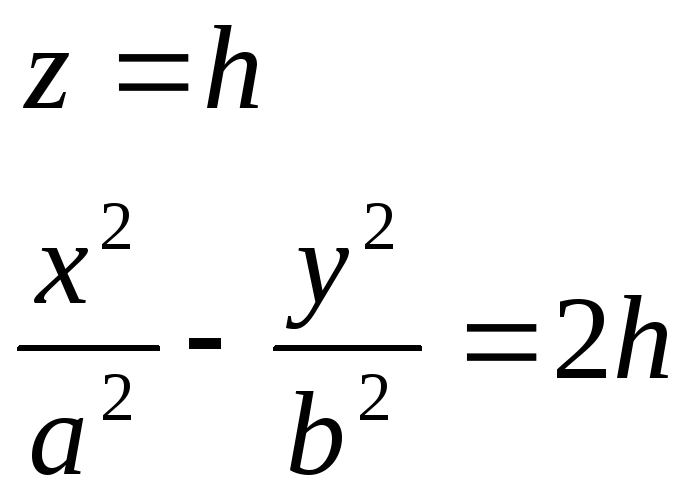
1.
![]() - гипербола.
- гипербола.
![]() .
.
2. h=0
![]()
![]()
![]() - пара пересекающихся прямых в начале
координат.
- пара пересекающихся прямых в начале
координат.
3.
![]() или
или
![]() - гипербола.
- гипербола.
II)
Пусть
![]() -
плоскость сечений и
-
плоскость сечений и
![]()
1.
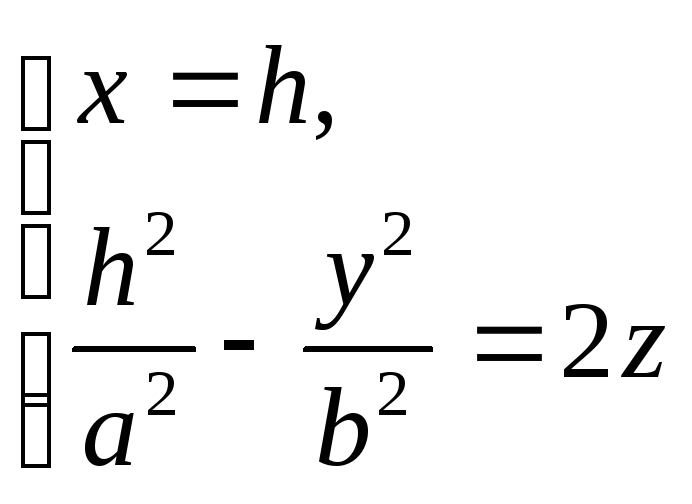
![]() - парабола, ветви которой направлены
вниз, симметричная относительно оси
Oz, с вершиной в начале
координат.
- парабола, ветви которой направлены
вниз, симметричная относительно оси
Oz, с вершиной в начале
координат.
При изменении h парабола либо смещается в начало координат, либо устремляется к бесконечности.
2. h=0
![]() -
парабола, направленная вниз, симметричная
относительно оси Oz,
с вершиной в начале координат.
-
парабола, направленная вниз, симметричная
относительно оси Oz,
с вершиной в начале координат.
III)
Пусть
![]() -
плоскость сечений и
-
плоскость сечений и
![]()
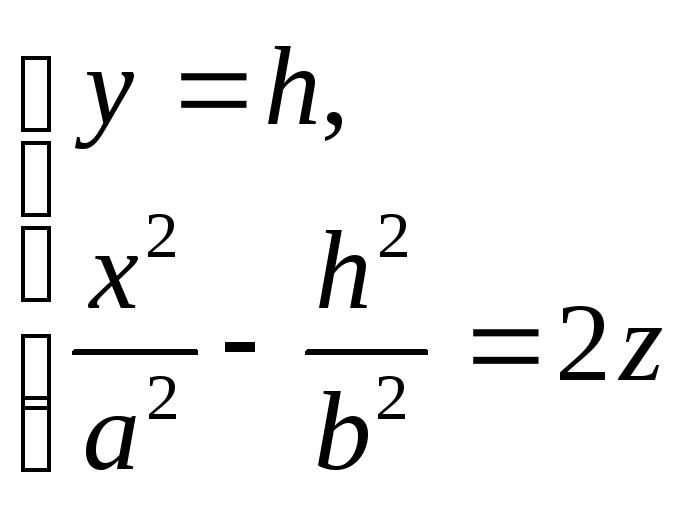
1. h=0
![]() - в сечении получается парабола,
направленная вверх, симметричная
относительно оси Oz,
с вершиной в начале координат.
- в сечении получается парабола,
направленная вверх, симметричная
относительно оси Oz,
с вершиной в начале координат.
2.
![]()
![]() или
или
![]() - уравнение задает направленную
вверх параболу.
- уравнение задает направленную
вверх параболу.