ГОСЫ / вопрос 8 / Лекция №9

Лекция 9

Коническая поверхность второго порядка. Цилиндрические поверхности.

Определение 9.1. Конической поверхностью с вершиной в точке О и направляющей называется множество точек пространства образованное всеми прямыми проходящими через точку О и пересекающими линию .

Вывод уравнения конической поверхности:

Пусть задана каноническая поверхность с вершиной в центе координат и плоскости z=h. Пусть она задана в этой плоскости уравнением:

z=h

Пусть - образующей конической поверхности. . Так как . т.к. .

- каноническое уравнение конической поверхности.

Определение 9.2. Конической поверхностью второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением (13)

Исследование конической поверхности методом сечений:

Коническая поверхность с началом в центре координат.

1. Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию

, распадающуюся на две пересекающиеся прямые

и

2. Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые: и

3.Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим:

или , из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями . При увеличении абсолютной величины h полуоси и также увеличиваются.

4. При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).

Цилиндрические поверхности второго порядка.

Определение 9.3. Поверхность, описываемая прямой, остающейся параллельной некоторому заданному направлению и пересекающей данную линию L , называется цилиндрической.

Определение 9.4. Цилиндрической поверхностью с направляющей и образующей параллельной вектору называется множество точек пространства, таких, что прямая проходящая через любую точку этого множества параллельна вектору и пересекает линию .

направляющая, образующая, .

Вывод уравнения цилиндрической поверхности:

Рассмотрим аффинную систему координат. Плоскость , - направляющая.

Так как лежит в xOy, значит уравнение линии примет вид:

. Пусть точка , но принадлежит образующей цилиндрической поверхности. Тогда образующая пересекает в точке . , .

. Выразим из третьего уравнения, получим . Подставим получившееся выражение в оставшиеся два уравнения.

. Подставим получившиеся значения X и Y в уравнение линии :

F (-)=0

F (, )=0

- уравнение цилиндрической поверхности.

Цилиндрические поверхности второго порядка определяются в прямоугольной системе координат Oxyz уравнениями:

• - эллиптический цилиндр. В частности при a=b - круговой, z- любое; (14) (рис. 1)

• - гиперболический цилиндр,

z- любое;

(15) (рис.2)

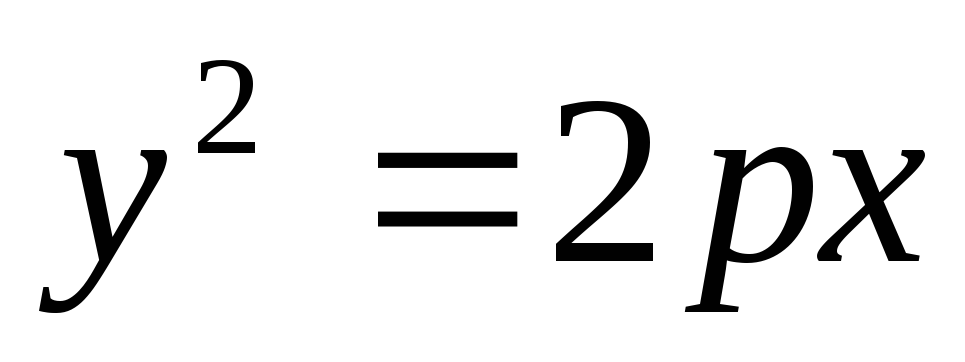• - параболический цилиндр, z- любое.

(16) (рис.3)

Уравнения (14)-(16) не содержат переменной z. На плоскости Оху уравнение (14) определяет эллипс с полуосями a и b. Если точка (х;у) лежит на этом эллипсе, то при любом z точка (х;у;z) лежит на поверхности, заданной каноническим уравнением (13). Совокупность таких точек есть поверхность, описанная прямой, параллельной оси Оz и пересекающей эллипс в плоскости Оху.

Этот эллипс называют направляющей линией данной поверхности, а все возможные положения движущейся прямой – образующими.

В случае гиперболического и параболического цилиндров ((15), (16)) направляющими линиями поверхностей являются гипербола и парабола, а образующими – прямые, параллельные оси Оz и проходящие через гиперболу и параболу в плоскости Ох.

5