Лекция 8.
Взаимное расположение двух и более прямых на плоскости. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Угол между прямыми
В аффинной системе
координат линия, заданная уравнением
первой степени, является прямой. Выясним,
при каких условиях два уравнения
и
:
I. Определяют одну и ту же прямую;
II. Определяют две параллельные прямые;
III. Определяют две пересекающиеся прямые.
I.
Условия, при которых уравнения
и
определяют
одну и ту же прямую.
Теорема 8.1.
Для
того чтобы два
уравнения
и
в аффинной системе координат определяли
одну и ту же прямую, необходимо и
достаточно, чтобы все коэффициенты в
уравнениях были пропорциональны.
Необходимость:
Дано: уравнения
прямой а:
(1)
(2)
Докажем:
.
Доказательство:
1. Данные уравнения
определяют одну прямую а.
Значит,
направляющие векторы
и 
будут коллинеарны, т.е.
или
.
2. Подставим
выражения в уравнение (1) и выразим
:
3. Найдем отношение
:
.
4. Значит,
Достаточность:
Дано: уравнения:
(1)
(2)
.
Докажем, что уравнения (1) и (2) задают одну и ту же прямую а.
Доказательство:
1. Выразим из условия
теоремы
коэффициенты
:
-
Подставим данные выражения в уравнение (1):
или
3. Значит, уравнениями (1) и (2) задаётся одна прямая в аффинной системе координат.
II. Условие параллельности двух прямых.
Теорема 8.2.
Два уравнения
и
в аффинной системе координат определяют
две параллельные прямые, если коэффициенты
при переменных
в
уравнениях пропорциональны.
Дано: уравнения
прямых а:
(1)
b:
(2)
Докажем:
.
Доказательство:
1. Данные уравнения
определяют две параллельные прямые а
и
b.
Значит, их
направляющие векторы
и 
будут коллинеарны, т.е.
или
.
2. Выразив коэффициент
пропорциональности, имеем:
.
III. Условие пересечения двух прямых.
Теорема 8.3.
Два уравнения
и
в аффинной системе координат определяют
две пересекающие прямые, если коэффициенты
при переменных
в
уравнениях не пропорциональны.
Дано: уравнения
прямых а:
(1)
b:
(2)
Докажем:
.
Доказательство:
Данные уравнения
определяют две пересекающие прямые а
и
b.
Значит, их
направляющие векторы
и 
не будут коллинеарными, т.е. них не
выполняется условие коллинеарности:
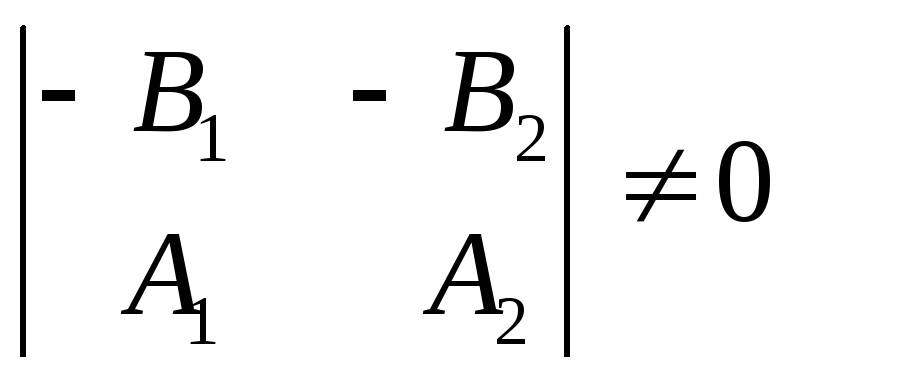или
Пучок прямых
Определение 8.4. Пучком прямых называется совокупность всех прямых плоскости, проходящих через некоторую точку S, называемую центром пучка.
Д
ля
задания пучка достаточно задать:
-
Его центр;
-
Две пересекающихся прямые.
1. Если известны координаты центра пучка S(x0,y0), то уравнение пучка примет вид:
2. Пусть прямые а и b пучка S заданы соответственно уравнениями:
(1)
(2)
.
Покажем, что
уравнение
(3) задает прямую, проходящую через S(x,y)
- точку пересечения прямых а
и b
Достаточно показать, что уравнение (3) является уравнением первой степени. Упростив уравнение (3), имеем:
(4)
Выражения
и
одновременно равняться нулю не могут,
т.к. в противном случае имеем:
и
.
Из равенства
следует, что прямые а
и b
параллельны,
что противоречит условию принадлежности
этих прямых пучку S.
Таким образом, уравнение (3) является уравнением первой степени и оно приводимо к уравнению (4), которое является общим уравнением прямой.
Пусть
уравнения
(3) не равно 0.
Поделим обе части уравнения на
и обозначим
.
Имеем:
- уравнение
пучка S
(уравнение произвольной прямой пучка
S), где
- параметр, однозначно определяющий
прямую пучка S.
Пример. Написать уравнение прямой l, проходящей через точку М(-2;6) и через точку пересечения прямых: x-3у+1=0
2x+4у =0.
I способ
1.Найдём точку
пересечения данных прямых
,
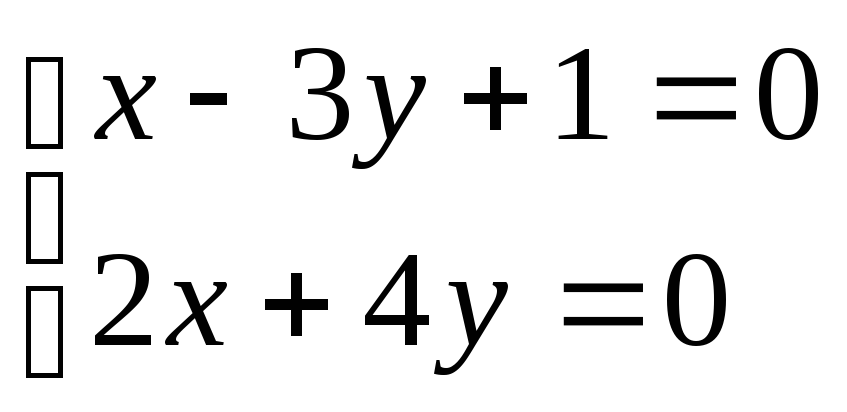
2.Напишем уравнение прямой l по двум точкам. М(-2;6) и М(-2/5;1/5).
29x+8у+10=0.
II способ
1. Две пересекающиеся прямые задают пучок. Запишем уравнение пучка:
2. Так прямая l
принадлежит пучку и проходит через
точку М(-2;6),
то
,
=19.
3. Подставив
значение
в уравнение пучка, получим уравнение
прямой l:
29x+8у+10=0
Расстояние от точки до прямой
Определение
8.5:
Ненулевой
вектор
называется
перпендикулярным
к прямой,
если он перпендикулярен любому
направляющему вектору этой прямой.
Лемма 8.6.
Если прямая
задана
в прямоугольной системе координат
уравнением
,
то вектор
будет
перпендикулярен этой прямой.
Определение
8.7.
Расстоянием
от точки
до прямой
называется длина перпендикуляра,
опущенного из этой точки на прямую
.
Дано:
:
,
М0(х0,у0)
.
Н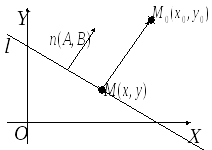
айти:
Решение:
1.
,
где
.
2. Т.к. прямая
задана в прямоугольной системе координат,
то по лемме
8.3
вектор
перпендикулярен
.
3. Из 1) и 2) следует,
что векторы
и
коллинеарны. Найдем их скалярное
произведение:
.
.
4. Т.к.
,
то её координаты удовлетворяют уравнению
прямой.
.
5. Из 3) и 4) следует,
что
.
Угол между прямыми
Будем рассматривать прямые а и b на положительно ориентированной плоскости.
Определение 8.8. Направленным углом между прямыми a и b называется направленный острый угол между их направляющими векторами.
1. Пусть прямые а
и
b
заданы в ортонормированном базисе
уравнениями:
,
.
Их направляющие векторы соответственно
имеют координаты:
,
Используя определения косинуса и синуса угла на ориентированной плоскости, найдем тангенс угла между прямыми а и b,
;
Таким образом,
Если прямые а
и
b
перпендикулярны,
то
.
2. Пусть прямые а
и
b
заданы в ортонормированном базисе
уравнениями:
,
.
Их направляющие векторы соответственно
имеют координаты:
,
.
Тогда
.
Условие
перпендикулярности прямых а
и
b
примет вид:
