ГОСЫ / вопрос 1 / Лекция №3

Лекция №3

Смешанное произведение векторов.

Геометрический смысл смешанного произведения. Объем тетраэдра

Определение 3.1. Смешанным (тройным) произведением некомпланарных векторов , взятых в определенном порядке, называется скалярное произведение вектора и вектора

Смешанное произведение в ортонормированном базисе.

Теорема 3.2. Если векторы , и в ортонормированном базисе имеют координаты , то смешанное произведение векторов вычисляется по формуле: .

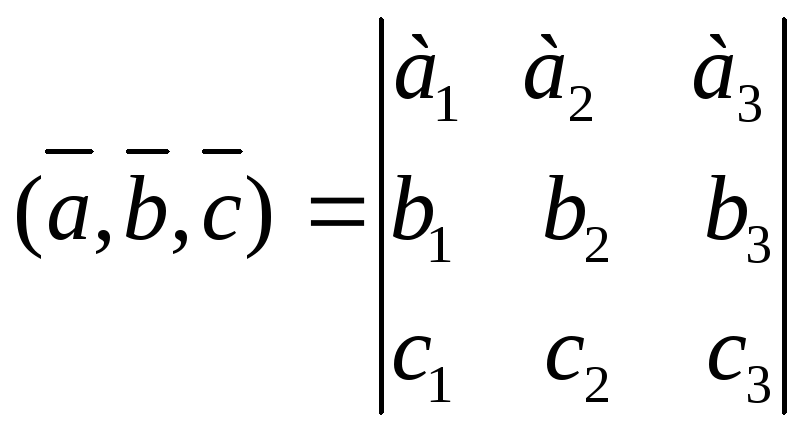Доказательство.

1. Выразим координаты вектора 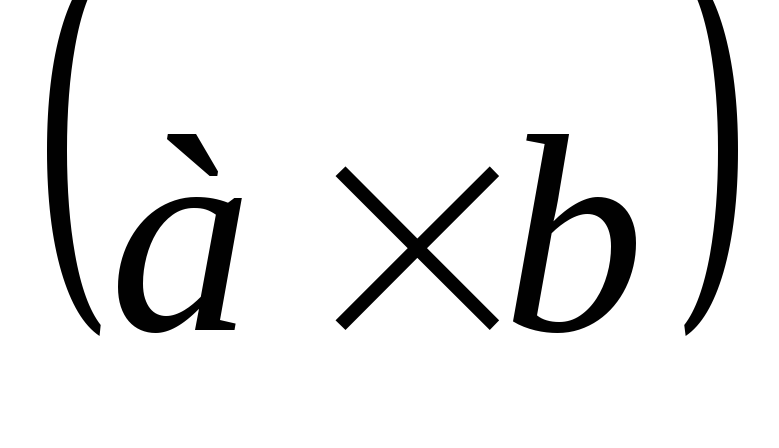в ортонормированном базисе.

По теореме 2.4 лекции 2 имеем: .

2. Выразим скалярное произведение векторов 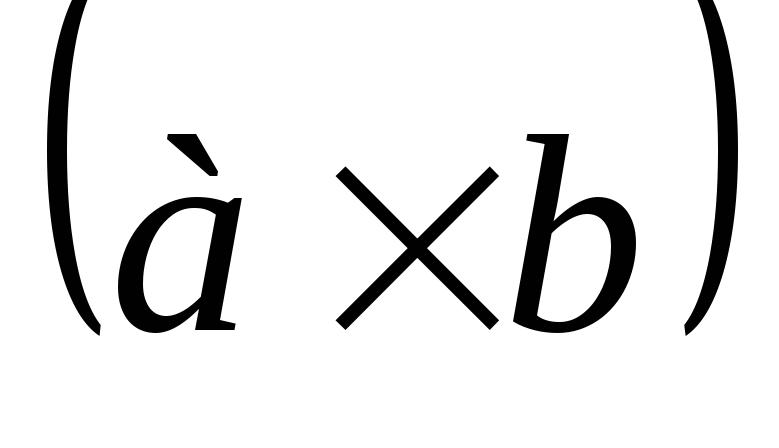и в ортонормированном базисе: = = =.

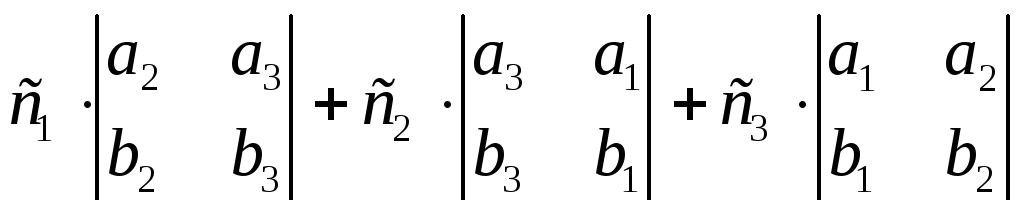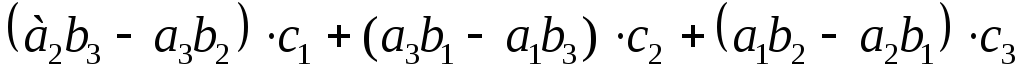3. Соберем правую часть равенства в определитель: 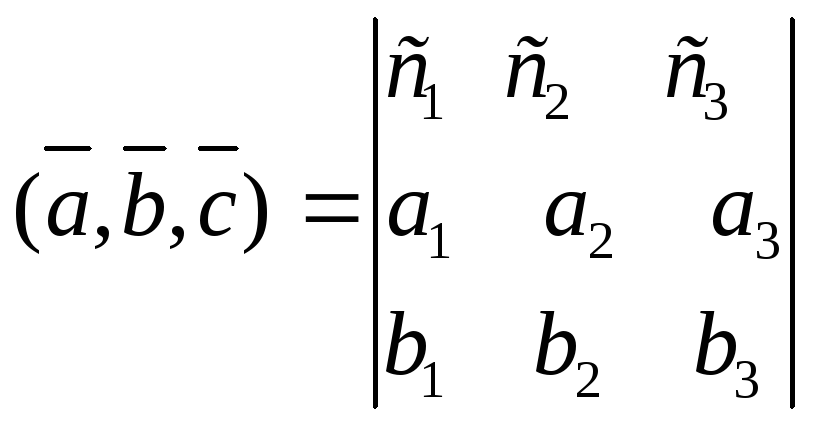. Перестановка двух любых строк определителя меняет его знак. Поменяв третью строку со второй, а затем новую вторую с первой, получим: .

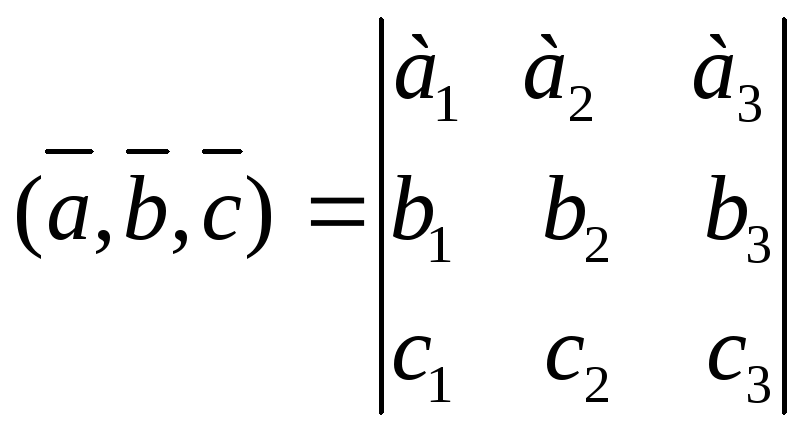Свойства смешанного произведения:

1. Если в смешанном произведении два любых вектора равны или коллинеарны, то оно равно нулю;

2. При перестановке местами двух множителей смешанное произведение меняет знак:

3. При циклической перестановке множителей смешанное произведение не меняется: (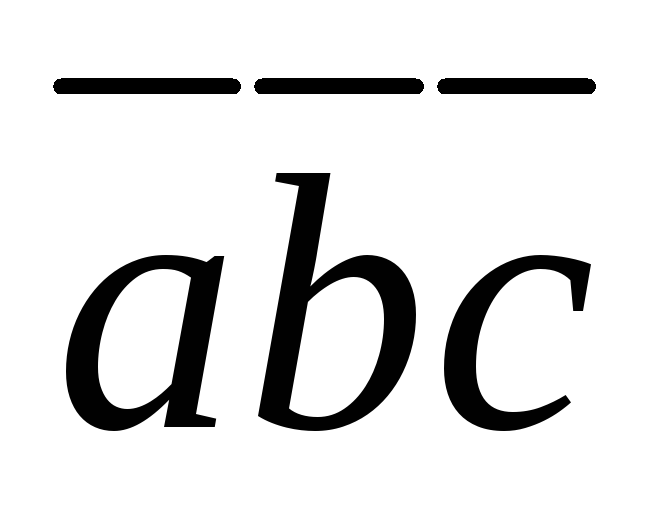)= 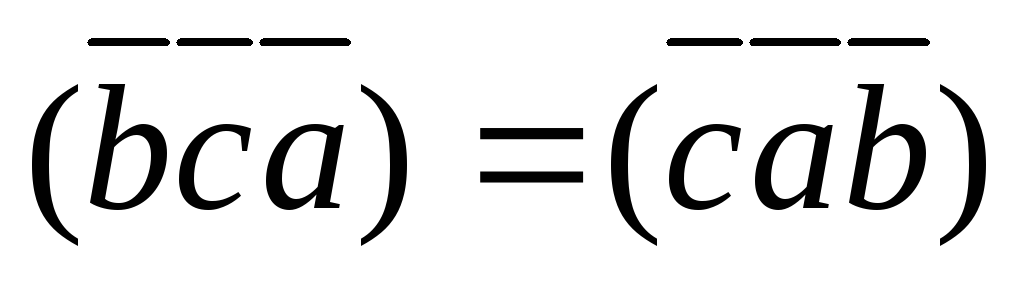(доказательство вытекает из того, что перестановка двух любых строк определителя меняет его знак).

4. Распределительное свойство смешанного произведения:

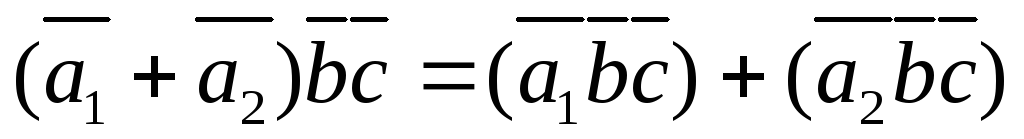
5. Сочетательное свойство смешанного произведения при умножении на скаляр:

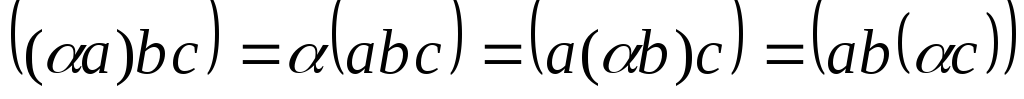
Геометрический смысл произведения трёх векторов

Теорема 3.3. Абсолютная величина смешанного произведения трех некомпланарных векторов равна объёму параллелепипеда, построенного на этих векторах.

Доказательство:

= , где

- площадь основания параллелепипеда,

- высота параллелепипеда, - объем параллелепипеда.

Значит, .

Замечание: Так будет всегда, если векторы , и образуют правую тройку. Если же векторы , и образуют левую тройку векторов, то их смешанное произведение будет отрицательно. В этом случае говорят, что параллелепипед, построенный на векторах , и рассматривается в отрицательно ориентированном пространстве, но его объем равен .

Замечание: Объем пирамиды, построенной на векторах , и , равен части объема параллелепипеда, построенного на этих же векторах, т.е. .

Задача 1. Пусть в пространстве даны четыре точки не принадлежащей одной прямой. А(1, -2, 7), В(0, 3, -2), С(3,1,0), (4,1,-1) . Найти объем пирамиды .

Теорема 3.4. Для того чтобы векторы , заданные в произвольном базисе (), были компланарны необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство:

1. Необходимость.

Пусть - компланарны, тогда они линейно зависимы, т.е. можно подобрать такие одновременно, что выполняется равенство:

(*)

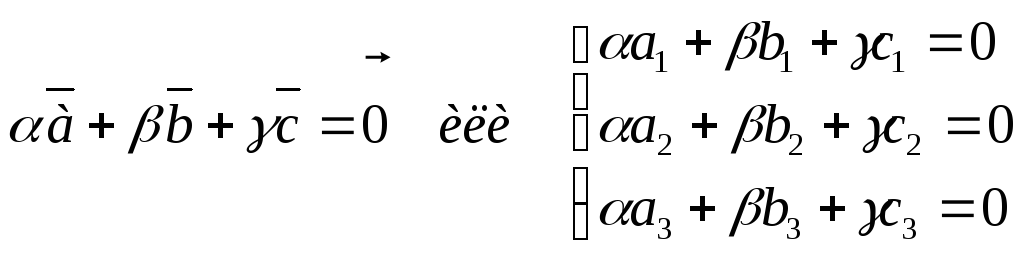Так как система является совместной, то определитель состоит из коэффициентов

перед неизвестными

II. Достаточность.

Пусть определитель равен нулю, тогда система (*) имеет единственное ненулевое решение. Умножим равенства системы соответственно на векторы и сложим получившиеся равенства:

система линейно зависима, тогда - компланарны.

Задача 2. Выяснить, лежат ли точки в одной плоскости?