
Лекция №16
Преобразование подобия. Гомотетия. Виды подобия.
Классификация подобий плоскости. Группа подобия и ее подгруппы.
Определение
16.1.
Преобразование
плоскости называется преобразованием
подобия, если
![]() k
> 0, что для
любых двух точек А
и
B
и их образов
A`
и B`
выполняется равенство
k
> 0, что для
любых двух точек А
и
B
и их образов
A`
и B`
выполняется равенство
![]() .
.
При k =1 преобразование подобия сохраняет расстояние, т.е. является движением. Значит, движение – частный случай подобия.
Определение
16.2.
Преобразование плоскости называется
гомотетией, если существует некоторое
число m![]() 1,
что для любых трех точек плоскости М,
М
1,
что для любых трех точек плоскости М,
М![]() ,
M`
выполняется условие
,
M`
выполняется условие
![]() .
.
Точка М![]() -
центр гомотетии, число m
– коэффициент гомотетии. Если m
> 0 –
гомотетия положительна, если m
< 0 –
гомотетия отрицательна.
-
центр гомотетии, число m
– коэффициент гомотетии. Если m
> 0 –
гомотетия положительна, если m
< 0 –
гомотетия отрицательна.
Теорема 16.3. Гомотетия есть подобие.
Доказательство:
-
Рассмотрим гомотетию
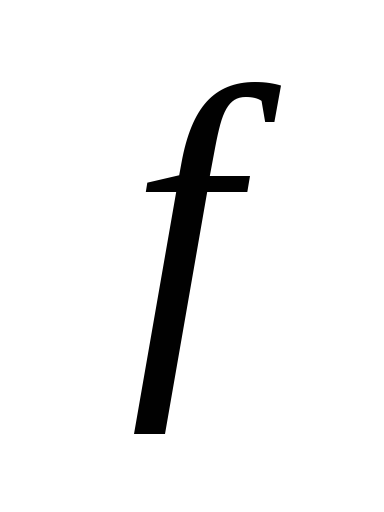 с центром
с центром
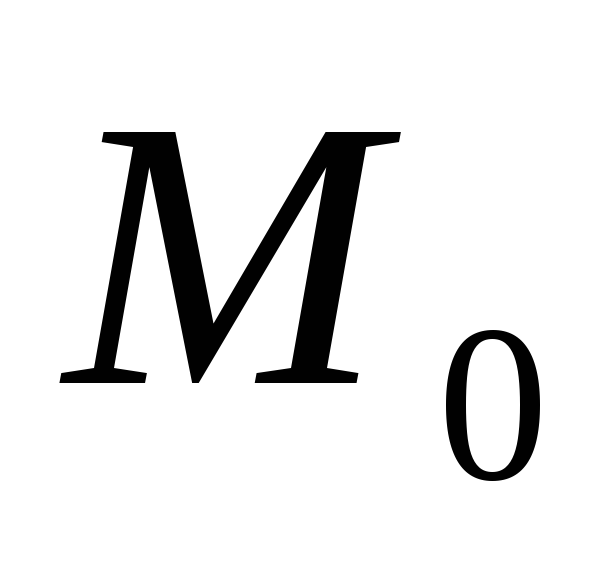 и коэффициентом m:
и коэффициентом m:
![]() ,
,
![]() .
.
2. По определению
гомотетии имеем:
![]()
3. Вычтем из
первого равенства второе:
![]() ,
,
![]()
 .
Значит, гомотетия
.
Значит, гомотетия
![]() есть подобие, где коэффициент гомотетии
есть подобие, где коэффициент гомотетии
![]() равен коэффициенту подобия
равен коэффициенту подобия
![]() .
.
-
Если m = 1, то гомотетия есть тождественное преобразование.
-
Если m =-1, то гомотетия есть центральная симметрия с центром в точке М
 .
. -
Если |m|
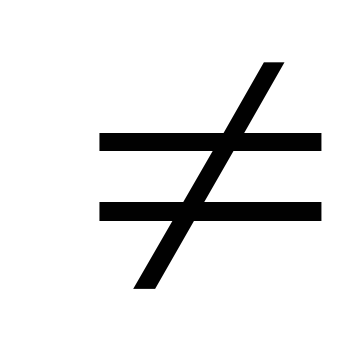 1,
то гомотетия есть преобразование
подобия, отличное от движения, т.е.
преобразование, не сохраняющее
расстояний.
1,
то гомотетия есть преобразование
подобия, отличное от движения, т.е.
преобразование, не сохраняющее
расстояний.
Если точка М
(x,
у) при
гомотетии
![]() переходит
в точку M`(x`,y`),
то:
переходит
в точку M`(x`,y`),
то:
![]() - аналитические
выражения гомотетии.
- аналитические
выражения гомотетии.
Свойства гомотетии
-
Гомотетия с коэффициентом, отличным от 1, переводит прямую, не проходящую через центр гомотетии, в прямую, ей параллельную; прямую, проходящую через центр – в себя.
-
Гомотетия сохраняет простое отношение трех точек.
-
Гомотетия сохраняет ориентацию плоскости.
-
Гомотетия переводит угол в равный ему угол.
Теорема 16.4.
Пусть f
– преобразование подобия с коэффициентом
k
> 0, а h
– гомотетия с коэффициентом
k
и центром в точке М![]() .
Тогда существует единственное движение
g
такое, что f
= g∙h.
.
Тогда существует единственное движение
g
такое, что f
= g∙h.
Доказательство:
-
Рассмотрим некоторое движение g, представимое как g = f h
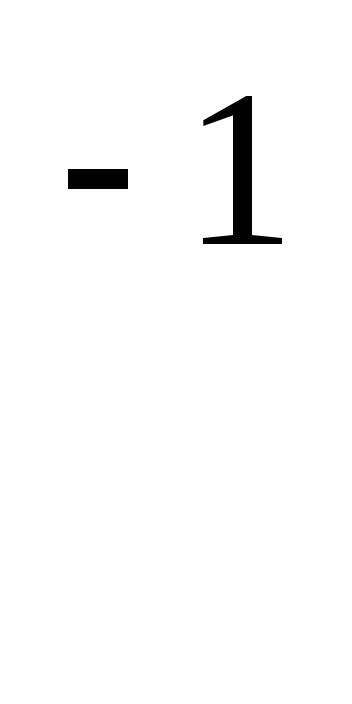 (*), где
(*), где
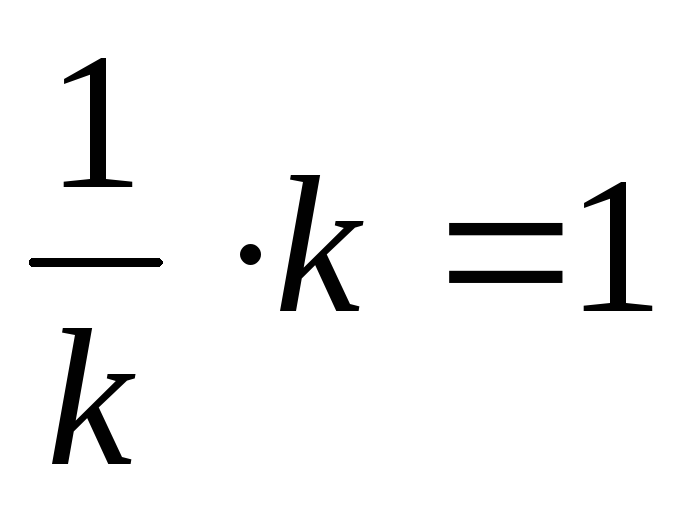 .
.
Рассмотрим
композицию движения
![]() и гомотетии
и гомотетии
![]() (помножим
обе части равенства (*) на гомотетию
(помножим
обе части равенства (*) на гомотетию
![]() ):
):
![]() или g∙h
= f
(**)
или g∙h
= f
(**)
-
Покажем, что движение
 единственно:
единственно:
-
Пусть существует движение g
 ,
такое, что
,
такое, что
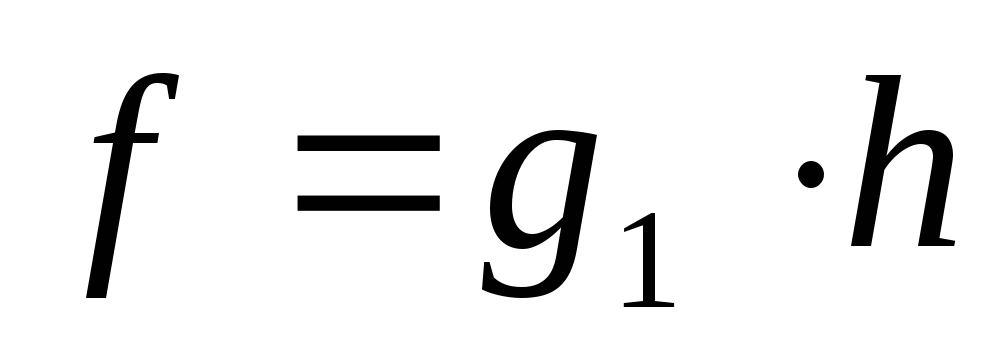 .
Тогда
.
Тогда
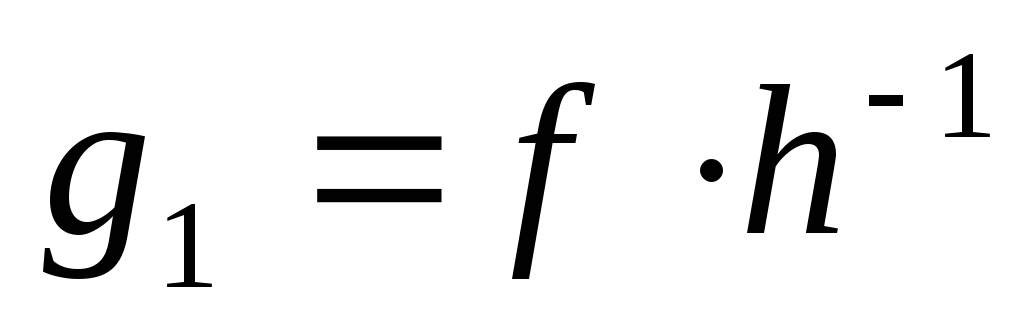 g
g =f
h
=f
h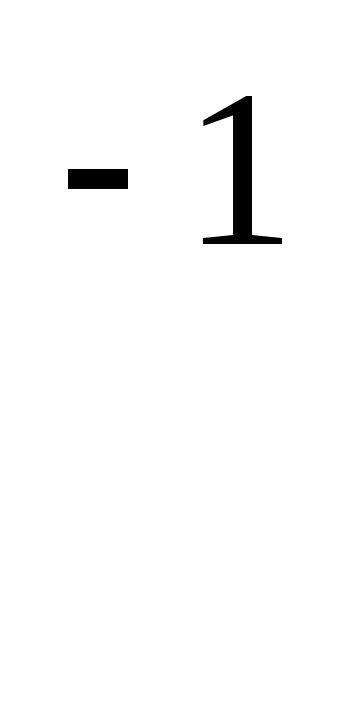 .
Но
.
Но
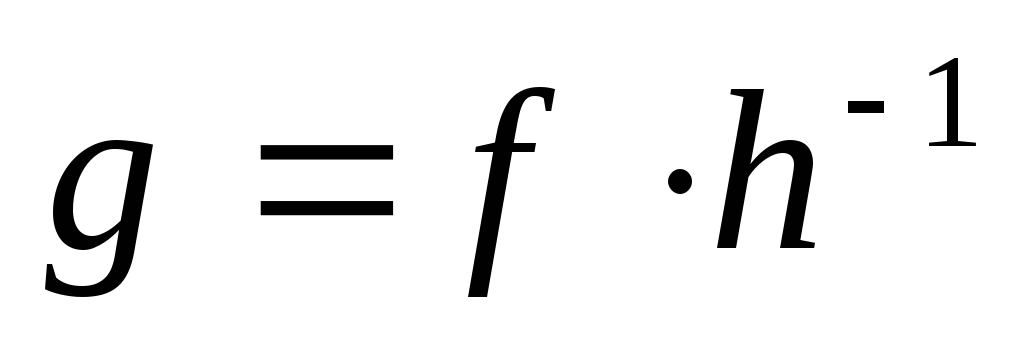 .
Значит, g
.
Значит, g =
g.
=
g.
Гомотетия обладает всеми свойствами движений, подобие также обладает всеми свойствами движений.
Так как гомотетия сохраняет ориентацию, а подобие есть произведение движения на гомотетию, т.е. движение имеет одну ориентацию с гомотетией, то подобие также имеет эту ориентацию. В этом случае говорят о подобии 1-го рода.
Если движение имеет ориентацию, противоположную гомотетии, то в этом случае подобие имеет противоположную ориентацию и является подобием 2-го рода.
Аналитические выражения подобия
Так как
гомотетия
![]() задается
выражениями
задается
выражениями
![]() ,
движение
,
движение
![]() задается
выражениями
задается
выражениями
![]() ,
то координаты образа
,
то координаты образа
![]() точки
точки
![]() в
преобразовании подобия
в
преобразовании подобия
![]() вычисляются по формулам:
вычисляются по формулам:
![]()
-
Если ε = 1, то подобие первого рода;
-
Если ε = -1, то подобие второго рода.
Теорема 16.5. Любое преобразование подобия имеет только одну неподвижную точку в том случае, если оно отлично от движения.
Доказательство:
1. Точка
![]() является
неподвижной точкой этого преобразования
тогда и только тогда, когда
является
неподвижной точкой этого преобразования
тогда и только тогда, когда
![]() .
Из аналитических выражений подобия
следует, что
.
Из аналитических выражений подобия
следует, что
![]()
![]()
Определитель
системы не равен 0 при ε = ± 1 . Таким
образом, при k
![]() 1
для любого
1
для любого
![]() имеем, что определитель не равен нулю
и, следовательно, система является
однородной, т.е. будет иметь единственное
решение.
имеем, что определитель не равен нулю
и, следовательно, система является
однородной, т.е. будет иметь единственное
решение.
Классификация подобия
Подобие первого рода.
-
Подобие имеет более чем одну неподвижную точку или не имеет неподвижных точек. Это подобие является движением (в частности параллельным переносом).
-
Подобие
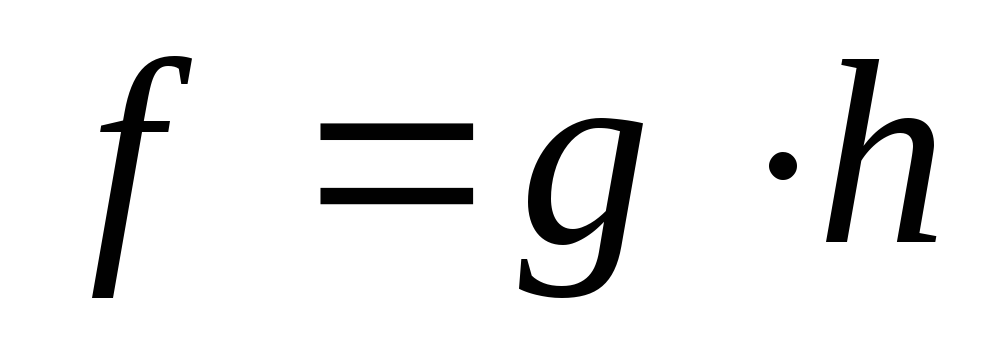 имеет
одну неподвижную точку.
имеет
одну неподвижную точку.
-
Так как f, h есть преобразования первого рода; g – тождественное преобразование, то подобие
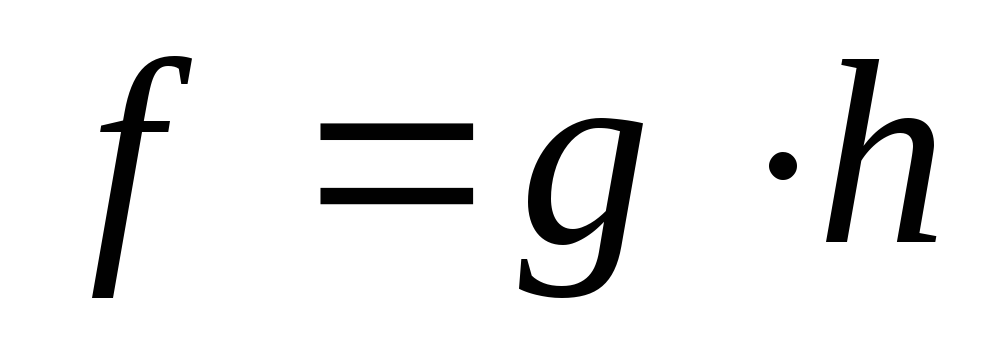 совпадает
с гомотетией.
совпадает
с гомотетией. -
Пусть g – центральная симметрия. Тогда подобие
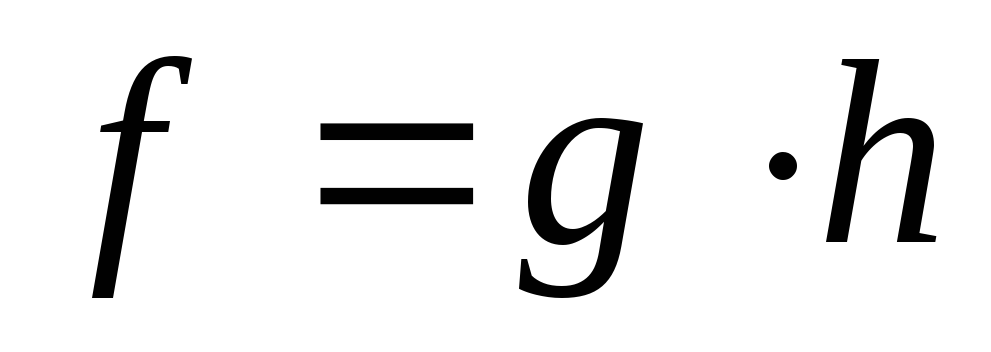 есть центрально подобное вращение на
угол
есть центрально подобное вращение на
угол
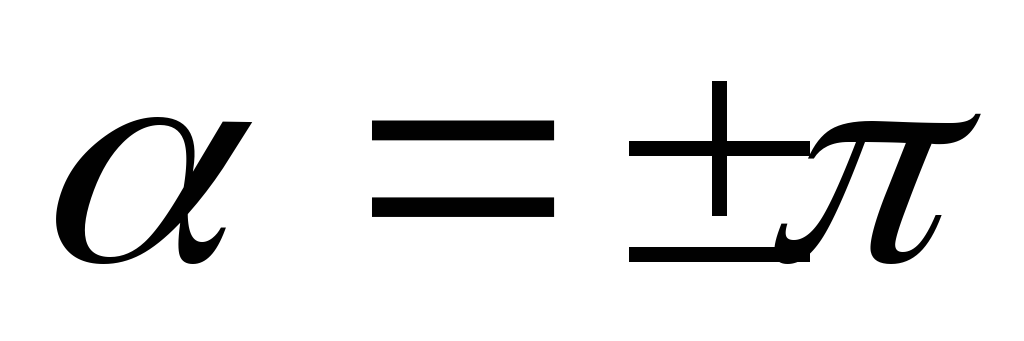 .
. -
Пусть g – поворот вокруг точки М
 .
Тогда подобие
.
Тогда подобие
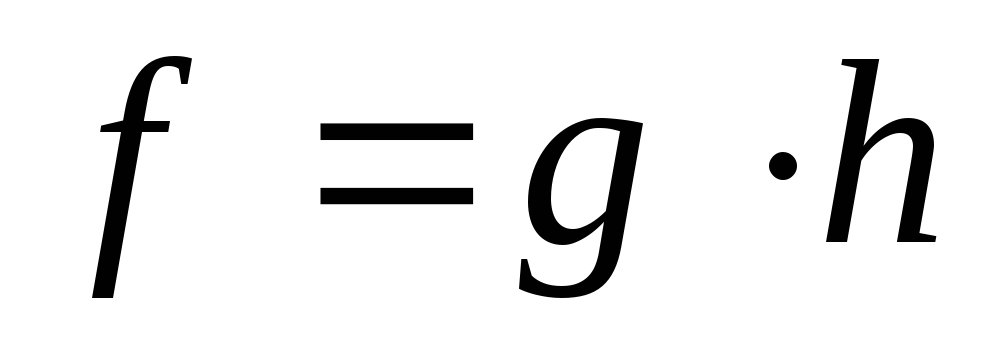 есть поворот с центром в точке М
есть поворот с центром в точке М .
.
Подобие второго рода.
-
Подобие имеет более чем одну неподвижную точку или не имеет вообще неподвижных точек. Подобие является либо осевой симметрией, либо скользящей симметрией.
-
Подобие имеет одну неподвижную точку O, k
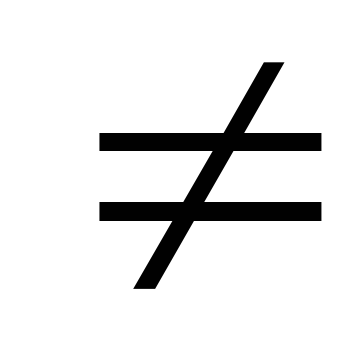 1.
Подобие f
называется центрально
подобной симметрией.
1.
Подобие f
называется центрально
подобной симметрией.
Следствие16.6. Любое преобразование подобия, имеющее более чем одну неподвижную точку или не имеющее неподвижных точек, является движением.
Группа подобия и ее подгруппы.
Пусть P – множество всех преобразований подобия плоскости, и на нем задана некоторая операция «∙».
Множество Р является группой относительно этой операции.
Действительно:
-
Если f
 ,
f
,
f
 P
, то f
P
, то f ∙ f
∙ f
 P
;
P
; -
Если f

 P
, то f
P
, то f

 P.
P. -
Основным инвариантом группы является мера угла.
Подобие первого рода образует подгруппу группы Р. Множество гомотетий с коэффициентом k (равным коэффициенту подобия) образует подгруппу группы Р.
Множество подобий второго рода не образует подгруппу, т.к. произведение подобий второго рода дает подобие первого рода.
