ГОСЫ / вопрос 15 / Лекция 7

Лекция 7

Вторая квадратичная форма. Кривизна кривой на поверхности. Индикатриса кривизны.

Пусть F – регулярная (гладкая) поверхность класса и поверхность F задается уравнением . – регулярная (гладкая) линия

1. При смещении точки М к М₁ получим вектор . Так как , то

(1)

2. – вектор нормали в точке М к поверхности F

– единичный вектор нормали.

3. Так как , то умножив равенство (1) скалярно на получим:

.

4. Пусть (4), тогда .

Учитывая 2, 3, 4, имеем, что

.

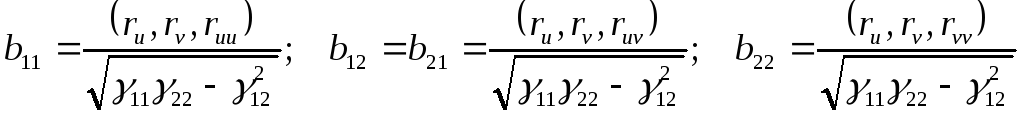Выражение вида: называется второй квадратичной формой поверхности.

Кривизна кривой на поверхности.

– естественная параметризация.

1. Найдем единичный вектор касательный к в точке М

(1)

2. По формуле Френе , тогда (2)

3. Умножим (2) скалярно на вектор нормали к поверхности

4. Учитывая значения имеем

(_*)

Определение 7.1. Сечение поверхности F, проходящее через нормаль к поверхности в точке М, называется нормальным сечением поверхности.

, и – единичные векторы.

Если нормальное сечение поверхности F, то или .

, так как при , а при .

Так как , то формула (_*) примет вид:

(_**).

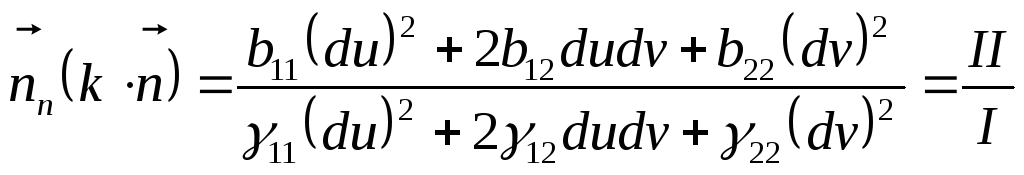Так как при и одновременно (в противном случае не было бы смещения точки М вдоль линии ), то можно положить, что .

Поделив равенство (_**) почленно на имеем:

.

Из формулы следует, что нормальная кривизна линии в точке М зависит только от направления касательной. Следовательно, все гладкие линии поверхности, проходящие через точку М и имеющие в этой точке общую касательную, имеют в точке М одну и ту же нормальную кривизну.

Значит, нормальная кривизна любой линии поверхности, проходящая через точку М с точностью до знака равна кривизне нормального сечения, имеющего с данной линией общую касательную.

Рассмотрим некоторую точку M поверхности F. Поверхность задана уравнением . Если в этой точке коэффициенты , то из формулы нормальной кривизны следует, что нормальная кривизна любой линии в этой точке равна нулю. В дальнейшем будем рассматривать случаи, когда хотя бы один из этих коэффициентов не равен нулю. Установим связь между нормальными кривизнами линий, проходящих через точку М и имеющих различные касательные.

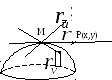Построим в точке М пучок прямых, лежащих в касательной плоскости к этой поверхности. В каждой из них будет касательная к определённой линии, проходящая через точку М.

По обе стороны точки М отложим отрезки

р

нормальная кривизна линии на поверхности.

авные , –

Определение 7.2. Линия, образованная концами отложенных отрезков называется индикатрисой кривизны или индикатрисой.

Введем в касательной плоскости аффинную систему координат, так чтобы точка М – начало системы координат, – координатные векторы.

Найдем уравнение индикатрисы в данной системе координат.

1. Пусть Р(х,у) – произвольная точка индикатрисы, принадлежащая , где – единичный вектор касательной МР к некоторой линии на поверхности, заданной уравнениями .

2. По определению индикатрисы имеем, что , так как единичный вектор касательной к линии , тогда

,

следовательно , .

3. выразим через и подставим выражения в формулу нормальной кривизны , имеем: – уравнение индикатрисы кривизны в точке М, где одновременно.

Уравнение индикатрисы определяет следующие действительные линии

1) – эллипс

2) – пара сопряженных гипербол

3) – пара параллельных прямых

4) – окружность