Лекция 6
Первая квадратичная форма. Длина дуги линии на поверхности. Угол между линиями на поверхности. Площадь куска поверхности.
Рассмотрим гладкую
линию F
класса Ск
заданную уравнением:
.Дифференциал
в т.М
имеет
вид:
Введем обозначение:
,
.
Наше равенство
примет вид :
(*)
Правая часть
полученной формулы представлена в виде
квадратичной формы (по определению),
эта квадратичная форма задана на
векторном пространстве ТМ0
касательной
к поверхности F
в т.M
является положительно определенной в
квадратичной форме т.к.
одновременно равняться нулю не могу и
(dF)2>0.
Определение 6.1. Квадратичная форма (*) называется первой квадратичной формой F или её линейным аргументом и обозначается I.
Коэффициенты
являются функциями криволинейных
координат на поверхности F.
Рассмотрим некоторую
линию
F
.
Для
Из этих равенств
,
что
Таким образом, значение первой квадратичной формы представляет собой дифференциала длины дуги гладкой линии, лежащей на поверхности при бесконечно малом смещении точки вдоль этой линии.
-
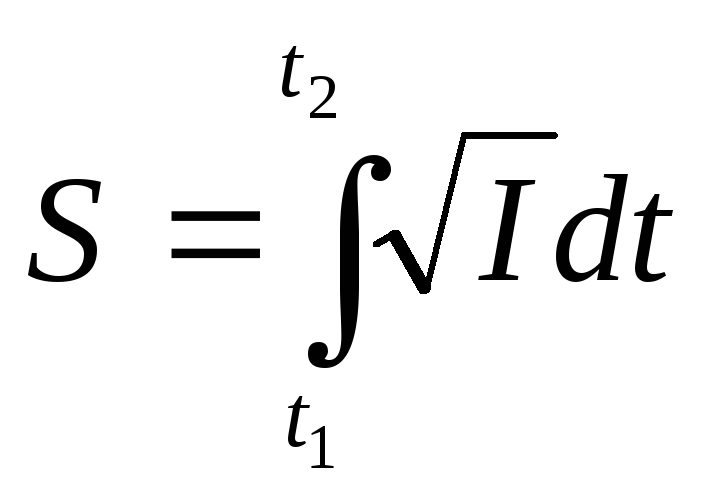длина дуги
Определение 6.2.
Углом между линиями
и
называется угол между касательными к
этим линиям всех общей точки.
-вектор касательной
к
-
вектор касательной к
1
=
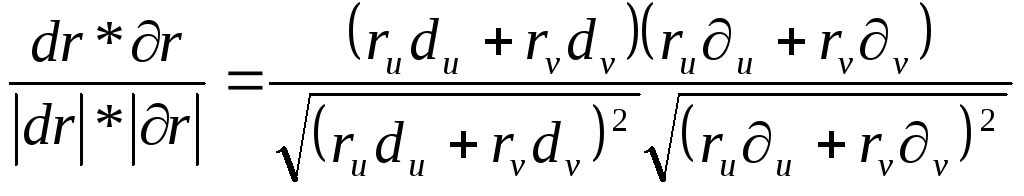-косинус
угла между линиями
Пусть
линия
(dv=0)
и 
линия
(dv=0)
=
Для того чтобы
и
–
линии были ортогональны, нужно чтобы
.
Пусть F поверхность с краем, удовлетворяющая трем условиям: F гомеоморфно замкнутому кругу; F является частью гладкой поверхности Ф; край поверхности F кусочно-гладкая линия
Для такой поверхности можно ввести понятие площади.
Определение 6.3. Поверхность, имеющая площадь называется квадрируемой.
Пусть регулярная
поверхность
задана уравнением
в прямоугольной системе координат.
Тогда
(1)
Если поверхность
F
задана параметрическими уравнениями
,
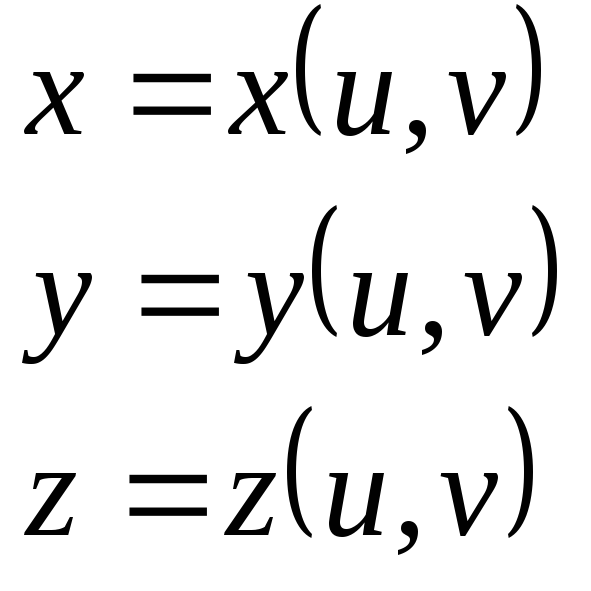то площадь этой поверхности вычисляется
по формуле
(2).
Доказательство (2) формулы
1)
2) выразим из этих
равенств
и
применяя формулы Крамера
3) найдем
,
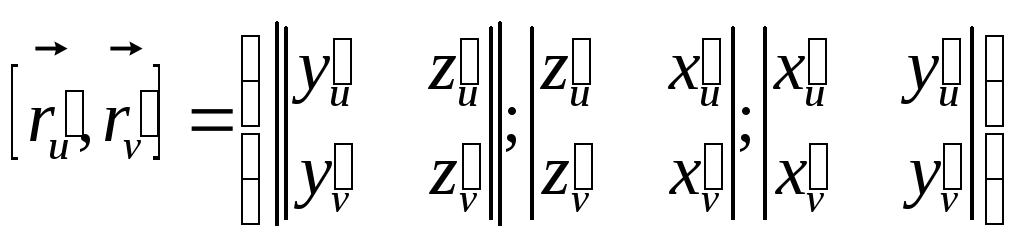где
,
где
.
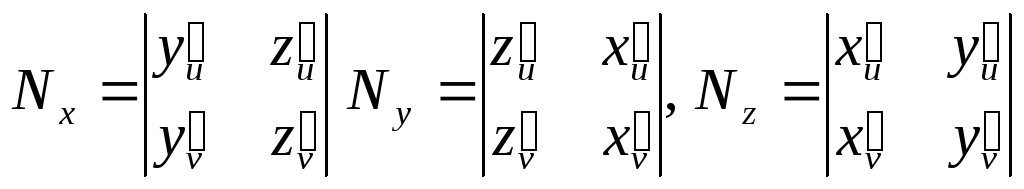4) из 2) и 3) следует
и
5) подставим
выражения
и
в формулу площади куска поверхности
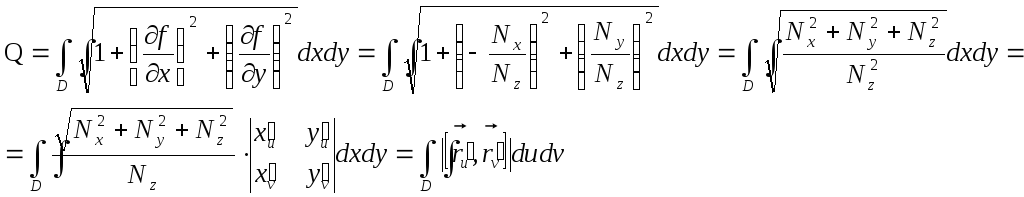
6) Покажем, что
.
.
Так
как
и
,
то
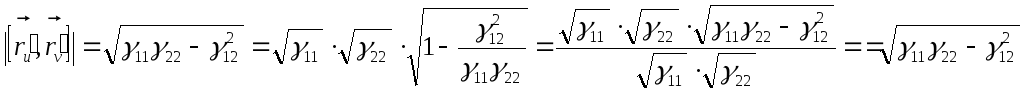Значит,
.