ГОСЫ / вопрос 5 / Лекция 9

Лекция №9

Эллипс. Каноническое уравнение. Исследование формы эллипса по его уравнению. Характеристические элементы эллипса. Параметрические уравнения эллипса. Способы построения эллипса. Эллипс как результат сжатия окружности к одному из ее диаметров

Пусть на плоскости даны две точки и , расстояние между которыми равно , и дано некоторое число , которое удовлетворяет условиям: или .

Определение 9.1. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух данных точек и есть величина постоянная, равная

Точки и называются фокусами эллипса, расстояние между ними обозначается через и называется фокусным расстоянием.

Введем прямоугольную систему координат таким образом, что ось пройдет через фокусы эллипса, ось - серединный перпендикуляр к отрезку .

1. Пусть

2. Точка является точкой эллипса тогда и только тогда, когда

3. ;

(1)

(2)

4. Покажем, что данное уравнение действительно есть уравнение эллипса – ведь пока мы доказали только, что каждая точка , удовлетворяющая уравнению (1) удовлетворяет и уравнению (2). Докажем обратное утверждение: каждая точка , удовлетворяющая уравнению (2), есть точка эллипса, т.е. для нее выполняется условие .

Найдем расстояния :

1. Выразим в координатах ;

2. Из уравнения (2) следует, что 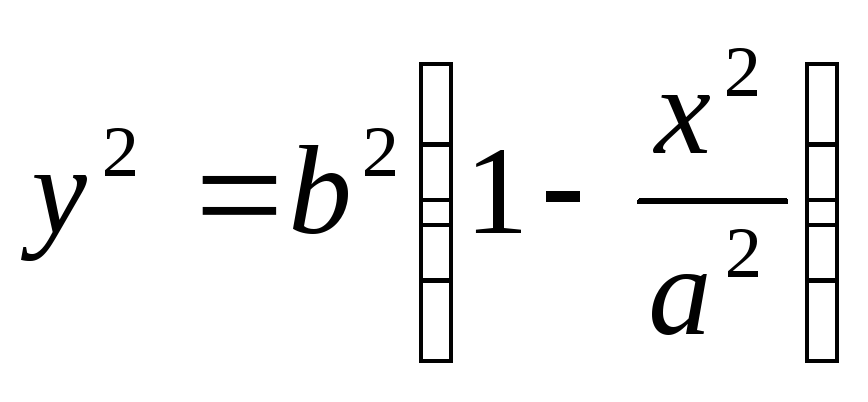. Так как , имеем ;

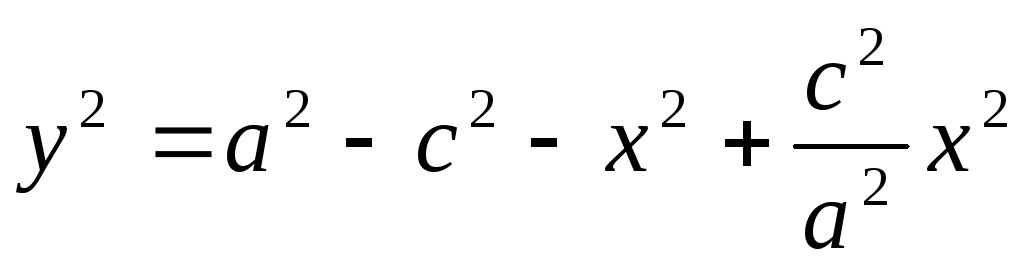3. Из (a) и (b) следует, что = . Так как , то .

4. Аналогичными рассуждениями приходим к выводу, что

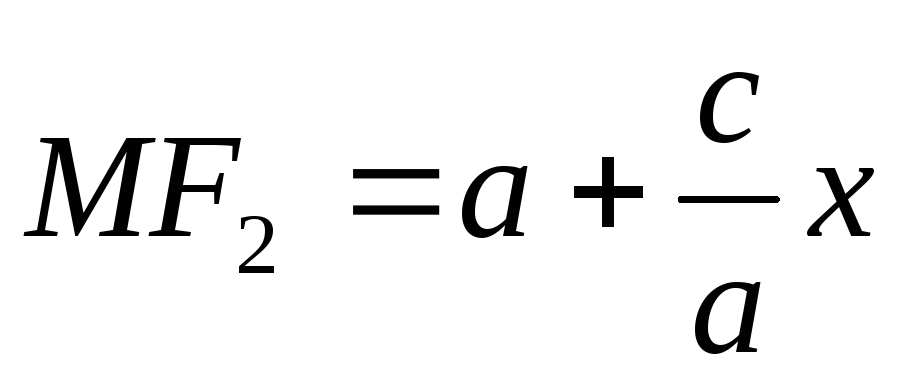
5. Найдем

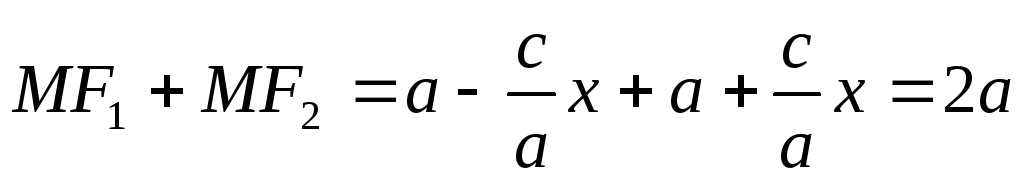
Таким образом, - каноническое уравнение эллипса

Исследование формы эллипса по каноническому уравнению

1. Эллипс – фигура ограниченная. Координаты точек эллипса ограничены неравенствами: . Это означает, что фигура эллипс есть ограниченная фигура, не выходящая за пределы прямоугольника со сторонами и .

Если точка эллипса принадлежит оси , то она имеет координаты . Если точка эллипса принадлежит оси , то она имеет координаты . Значит, неравенства, определяющие эллипс, имеют вид: .

2. Эллипс – фигура симметричная. В уравнение входят только чётные степени координат. Значит, эллипс есть линия, симметричная относительно осей координат и начала координат. Ось, проходящая через фокусы эллипса, называется первой или фокальной осью симметрии, а перпендикулярная к ней ось – второй осью симметрии.

Поэтому для исследования эллипса его достаточно рассмотреть в I четверти.

Для I четверти получаем, что . При возрастании от до , монотонно убывает от до .

3. Каждая ось симметрии пересекает эллипс в двух точках: , , , – вершины эллипса. Отрезки и называются осями эллипса. - большая ось, - малая ось. Начало координат – центр эллипса. Отрезки , , , – полуоси эллипса, причём – большие полуоси; – малые полуоси.

4. Когда фокусы эллипса расположены на оси , имеем, что . Когда фокусы располагаются на оси , , тогда .

Определение 9.2. Эксцентриситетом эллипса называется число, равное отношению фокусного расстояния к длине большей полуоси и обозначается: .

Так как .

От значения эксцентриситета зависит форма эллипса. Действительно, выразим отношение через эксцентриситет: . Имеем, что .

Чем ближе эксцентриситет к нулю, тем больше и при , эллипс похож на окружность. При увеличении эксцентриситета эллипс вытягивается вдоль оси .

Определение 9.3. Фокальными радиусами точки , принадлежащей эллипсу, называются отрезки, соединяющие эту точку с фокусами и .

Для каждой точки эллипса существует два фокальных радиуса.

Обозначаются: ,

.

Определение 9.4. Фокальным параметром называется длина отрезка , если он перпендикулярен оси и обозначается:

Пусть , значит . Т.к. , то ;

Таким образом, фокальный параметр равен отношению квадрата малой полуоси эллипса к его большой полуоси.

Определение 9.5. Директрисами эллипса называются две прямые: .

Так как эксцентриситет эллипса меньше 1, то директрисы, параллельные оси , находятся вне эллипса.

Директриса и фокус считаются соответствующими, если они расположены по одну сторону от центра фигуры.

Геометрический смысл эксцентриситета эллипса

Теорема 9.6. Отношение расстояния от каждой точки , принадлежащей эллипсу, до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету.

Доказать:

Доказательство:

1. Выразим ;

2. Выразим

1. Найдем отношение:

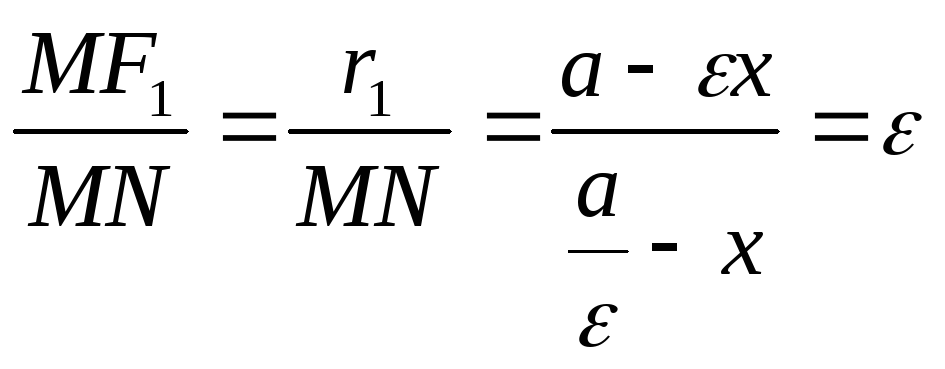
4. Аналогично доказывается, что

Параметрические уравнения эллипса.

1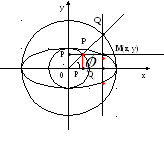. Пусть в прямоугольной системе координат задан эллипс своим каноническим уравнением , причём .

2. Начертим в этой системе координат

две окружности: и .

3. Рассмотрим - прямоугольные и

выразим координаты , принадлежащей

эллипсу:

:

:

4. Подставим полученные выражения в уравнение эллипса:

_.

Таким образом, этот эллипс можно задать уравнениями вида:

- параметрические уравнения эллипса.

Способы построения эллипса

Способ №1 (в основу положено определение 9.1)

В чертежную доску вбиваются два гвоздика и с расстоянием . В них фиксируются концы нити длиной . Натянув эту нить приложением к ней острия карандаша, передвигают карандаш так, чтобы нить все время была натянутой. При этом карандаш вычертит эллипс, как геометрическое место точек, сумма расстояний каждой из которых до двух данных точек и есть величина постоянная, равная

Способ №2 (в основу положено определение 9.1)

Так как эллипс есть геометрическое место вершин треугольников, имеющих общее основание 2с и данную сумму двух других сторон 2а, то необходимо построить множество треугольников с общей вершиной по стороне и сумме двух других сторон, при этом всякий раз задавая угол .

Способ №3 (в основу положено свойство симметричности эллипса): построить по точкам часть эллипса в первой четверти, используя уравнение, а затем использовать симметричность линии относительно осей координат и начала координат.

Способ №4 (по заданным полуосям):

1. Построить две окружности с центром в начале координат и радиусами, равными полуосям эллипса: 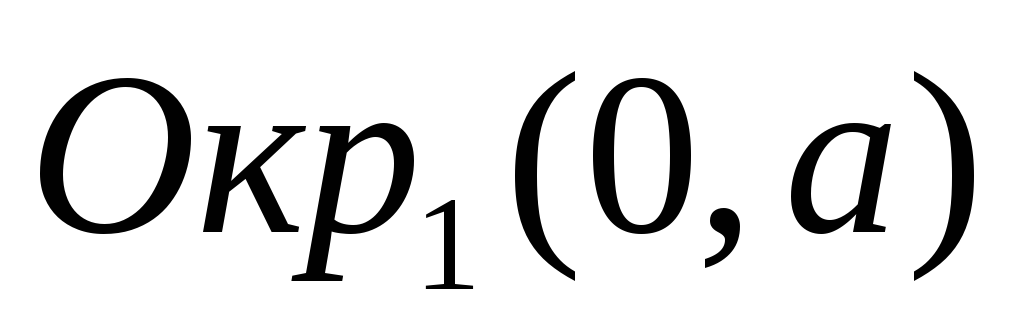_{и ;}

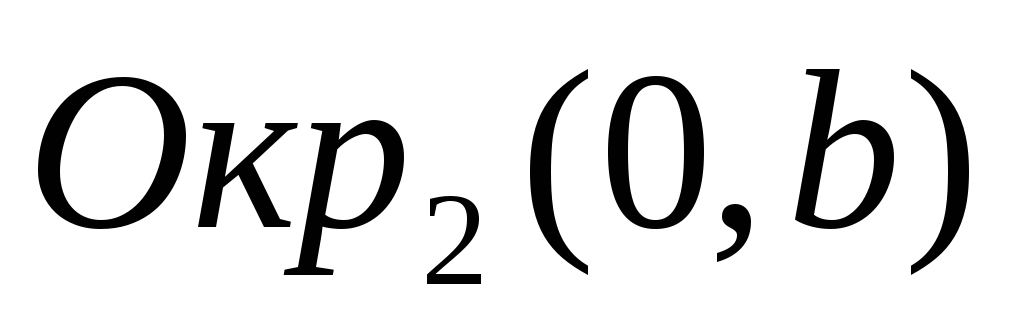2. Проведем из начала координат луч, пересекающий каждую окружность соответственно в точках , ;

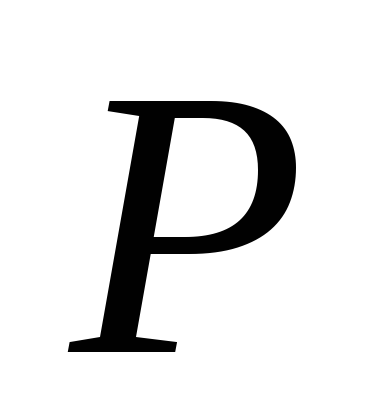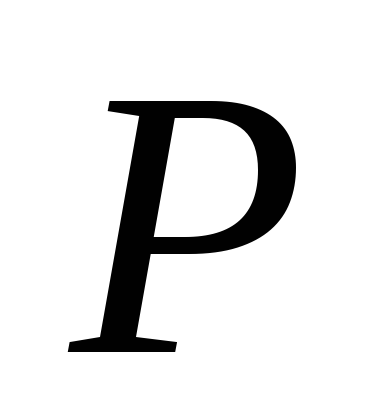3. Через точку проведем прямую , параллельно оси , через точку - прямую 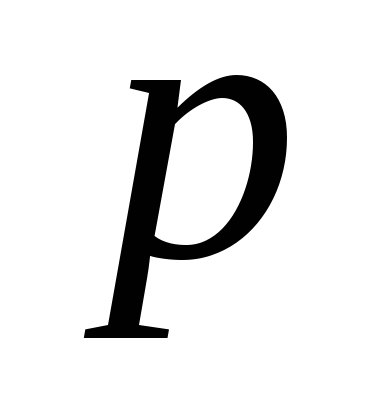, параллельную оси ;

4. Точка пересечения прямых и – точка эллипса ;

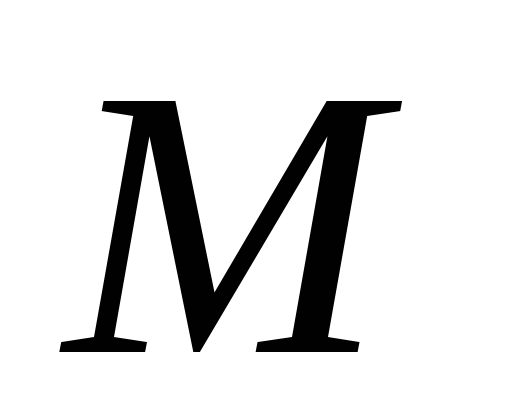5. Аналогичные действия проводим при построении следующего луча, проходящего через начало координат.

Эллипс как результат сжатия окружности к одному из ее диаметров

Способ №3 построения доказывает одно важное наглядное свойство эллипса. Действительно, - произвольная точка эллипса, а есть точка большой окружности, имеющая ту же абсциссу, т.е. лежащая на той же вертикальной прямой, что и . Тогда , .

Из подобия : или

Таким образом, эллипс получился из «большой» окружности преобразованием плоскости: каждая точка большой окружности переходит в точку эллипса с той же абсциссой, но с ординатой, полученной из ординаты точки умножением на число .

Такое преобразование называется равномерным сжатием плоскости к оси абсцисс в отношении .

Таким образом, обосновывается следующее утверждение: всякий эллипс получается сжатием окружности к одному из ее диаметров.