Контрольная работа №1

«Введение в математический анализ»

ВАРИАНТ 0

Доказать по определению Коши

1. 2.

Вычислить пределы

3. 4. 5.

6. 7.

8. 9.

10. Вычислить односторонние пределы функции в точках :

.

Нарисовать график функции в окрестности этих точек.

Вычислить пределы

11. 12.

Примеры решения задач

Пример 1.

Доказать, пользуясь определением по Коши предела функции в точке, что .

Решение.

По определению предела функции в точке ( по Коши):

>0 >0: x: 0<|x-1|<  .

Выберем произвольное число >0. Найдем для него число >0, такое, что для всех х, удовлетворяющих условию 0<|x-1|< выполнено неравенство . Преобразуем левую часть:

.

Значит, неравенство 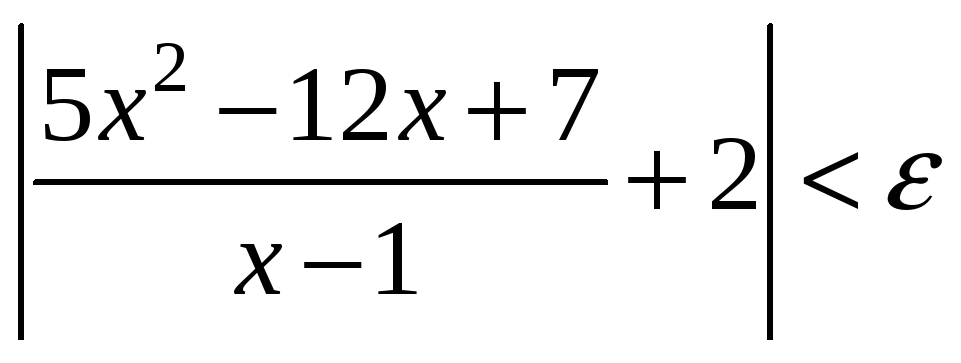равносильно неравенству. Отсюда . Поэтому в качестве  можно взять число . При таком  из условия 0<|x-1|< будет следовать неравенство .

Таким образом, показано, что >0 =: x: 0<|x-1|<  . Это значит, что .

Пример 2.

Вычислить предел .

Решение.

Для раскрытия имеющейся здесь неопределенности вида применим следующий прием: разделим числитель и знаменатель дроби на старшую степень n. В данном случае надо разделить на n³. Получим

.

Использовали тот факт, что величины , , , , являются бесконечно малыми при n, следовательно, их предел равен нулю.

Пример 3.

Вычислить предел .

Решение.

В этом примере в скобке имеем неопределенность вида -. Чтобы избавиться от нее, применим следующий прием: умножим и разделим на выражение, сопряженное выражению в скобках. В данном случае умножим на и в числителе получим разность квадратов. Упростив, придем к неопределенности вида , которую раскроем, как в предыдущем примере, делением на старшую степень n (на ).

======.

Пример 4.

Вычислить предел .

Решение.

В данном примере используется определение факториала натурального числа. Факториалом числа nназывается произведение всех натуральных чисел от 1 до n включительно: n!=123n. Например, 1!=1, 2!=12=2, 3!=123=6 и т. д. По определению 0!=1.

В пределах такого вида приходится выражать факториалы бóльших чисел через факториал меньшего числа. В данном случае меньшим числом является (3n-1). По определению факториала можем записать:

.

Значит, (3n+1)!=(3n-1)!(3n)(3n+1), а (3n)!=(3n-1)!(3n).

Выразим факториалы указанным образом через (3n-1)! и сократим дробь на (3n-1)! Затем раскроем скобки в числителе и знаменателе и разделим на старшую степень n (на n³).

====.

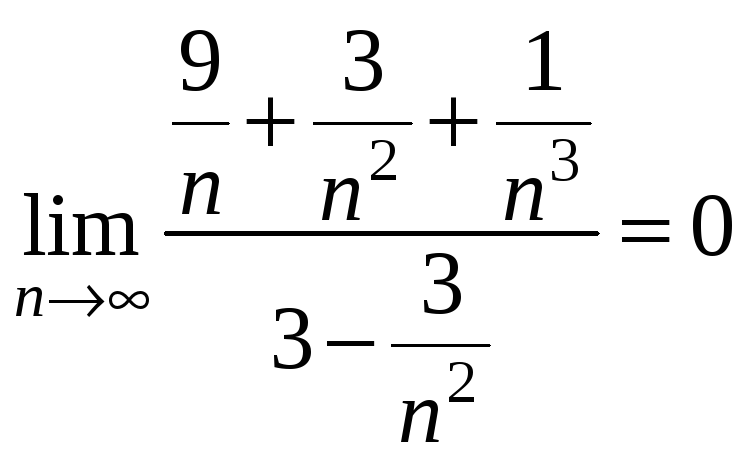Пример 5.

Вычислить предел .

Решение.

Применим следующий прием: разделим числитель и знаменатель на старшую степень бóльшего по модулю числа. Заметим, что в данном примере можно делить на 5ⁿ⁺² или на 5ⁿ⁺¹ или на 5ⁿ. При этом используется известный предел:

Удобнее делить числитель и знаменатель на 5ⁿ.

==.

Пример 6.

Вычислить предел .

Решение.

Так как предел основания , а предел показателя степени , то в данном случае имеем неопределенность 1^. При вычислении пределов такого вида используется второй замечательный предел: . Вместо n здесь может стоять любая бесконечно большая величина, то есть , где .

Выделим вначале в основании целую часть. Для этого получим в числителе выражение, равное знаменателю и разделим почленно числитель на знаменатель.

==.

В нашем случае . В показателе выделим выражение и затем используем свойство .

===

=.

Пример 7.

Вычислить предел .

Решение.

Числитель и знаменатель данной дроби стремятся к нулю при х10. Для раскрытия имеющейся здесь неопределенности разложим числитель и знаменатель на множители и разделим на выражение (х-10). Для этого в числителе применим формулу разности кубов: , а в знаменателе вынесем х за скобки и свернем квадрат разности:

.

Числитель получившейся дроби стремится к 300, а знаменатель – к нулю, т. е. является бесконечно малой величиной. Значит, дробь является бесконечно большой величиной и

.

Пример 8.

Вычислить предел .

Решение.

В данном случае имеется неопределенность . Умножим числитель и знаменатель дроби на выражение, сопряженное числителю, и на выражение, сопряженное знаменателю:

.

Пример 9.

Вычислить предел .

Решение.

При х0 sinx0, 3xsinx0, x²0. Значит, можно заменить числитель и знаменатель дроби эквивалентными бесконечно малыми: , . Тогда получим

.

Пример 4.

Вычислить предел .

Решение.

В данном случае выражение, стоящее под знаком синуса, не является бесконечно малым: . Поэтому вначале необходимо раскрыть в этом выражении скобки и затем применить формулу приведения: . Получим

.

Теперь можно заменить числитель и знаменатель эквивалентными бесконечно малыми: , при х0. Тогда

.

Пример 10.

Вычислить предел .

Решение.

Пример 11.

Вычислить предел .

Решение.

Выражение, стоящее под знаком предела, является показательно-степенной функцией , где , . Вычислим пределы основания и степени:

, .

Тогда используя правило предел степени равен степени пределов (в данном случае нет неопределенности), получим

.

Пример 12.

Вычислить предел .

Решение.

В этом примере предел основания , предел показателя . Значит, имеется неопределенность 1^. Воспользуемся вторым замечательным пределом в следующей форме записи:. Выполним преобразования, как в примере 5 из задания 2:

.

Пример 13.

Исследовать на непрерывность функцию .

Решение.

Функция является элементарной как отношение двух многочленов, значит, она непрерывна во всех точках своей области определения. Областью определения является множество всех точек числовой прямой, за исключением тех, в которых знаменатель обращается в нуль. Найдем нули знаменателя: x²-6x+5=0  x=1 и x=5.

Итак, , данная функция непрерывна на . Точки х=1 и х=5 являются точками разрыва. Исследуем характер разрыва. Для этого найдем односторонние пределы функции в точках х=1 и х=5.

,

,

,

,

В точках х=1 и х=5 функция имеет бесконечные односторонние пределы. Следовательно, эти точки являются точками разрыва второго рода.