
IDZ1_GEOMETRIYa (1)
.docx3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
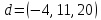 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
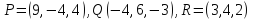 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 24.
1.
Даны векторы

2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
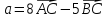 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
 на вектор
на вектор
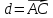 ;
г) координаты точки М,
делящей отрезок BC
в
отношении
;
г) координаты точки М,
делящей отрезок BC
в
отношении

3.
Доказать, что векторы
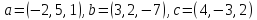 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
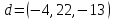 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
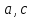 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
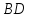 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
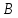 .
.
Вариант 25.
1.
Даны векторы
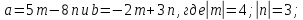

2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
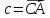 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок BC
в
отношении
;
г) координаты точки М,
делящей отрезок BC
в
отношении
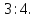
3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
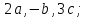 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
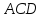 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 26.
1.
Даны векторы

2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
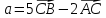 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок AB
в
отношении
;
г) координаты точки М,
делящей отрезок AB
в
отношении
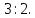
3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
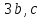 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.
 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 27.
1.
Даны векторы


2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок BC
в
отношении
;
г) координаты точки М,
делящей отрезок BC
в
отношении

3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
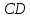 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
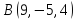 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 28.
1.
Даны векторы


2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
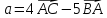 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
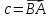 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок BA
в
отношении
;
г) координаты точки М,
делящей отрезок BA
в
отношении

3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
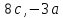 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
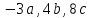 .
.
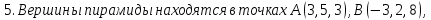
 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
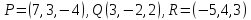 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 29.
1.
Даны векторы

2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
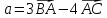 и
и
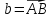 ;
в) проекцию вектора
;
в) проекцию вектора
 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок BA
в
отношении
;
г) координаты точки М,
делящей отрезок BA
в
отношении

3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

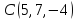 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
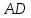 и вершины пирамиды
и вершины пирамиды
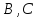 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
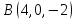 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
Вариант 30.
1.
Даны векторы

2.
По координатам точек
 для указанных векторов найти: а) модуль
вектора
для указанных векторов найти: а) модуль
вектора
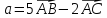 ;
б) скалярное произведение векторов
;
б) скалярное произведение векторов
 и
и
 ;
в) проекцию вектора
;
в) проекцию вектора
 на вектор
на вектор
 ;
г) координаты точки М,
делящей отрезок AB
в
отношении
;
г) координаты точки М,
делящей отрезок AB
в
отношении

3.
Доказать, что векторы
 образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
 в этом базисе.
в этом базисе.
4.
Даны векторы
 .
Необходимо: а) вычислить смешанное
произведение трех векторов
.
Необходимо: а) вычислить смешанное
произведение трех векторов
 б) найти модуль векторного произведения
б) найти модуль векторного произведения
 в) вычислить скалярное произведение
двух векторов
в) вычислить скалярное произведение
двух векторов
 ;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
;
г) проверить, будут ли коллинеарны или
ортогональны два вектора
 ;
д) проверить, будут ли компланарны три
вектора
;
д) проверить, будут ли компланарны три
вектора
 .
.

 и
и
 .
Вычислить: а) площадь грани
.
Вычислить: а) площадь грани
 ;
б) площадь сечения, проходящего через
середину ребра
;
б) площадь сечения, проходящего через
середину ребра
 и вершины пирамиды
и вершины пирамиды
 ;
в) объем пирамиды
;
в) объем пирамиды

6.
Даны три силы
 ,
приложенные к точке
,
приложенные к точке
 .
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: а) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
 ;
б) величину момента равнодействующей
этих сил относительно точки
;
б) величину момента равнодействующей
этих сил относительно точки
 .
.
