
- •Индивидуальное домашнее задание по дискретной математике
- •5. Выяснить взаимное расположение множеств d, e, f, если а, в, х – произвольные подмножества универсального множества u.
- •6. Упростить выражение.
- •8. Для данного графика р найти: р-1, р°р, р-1°р, пр2(р-1°р) ´ пр1(р°р).
- •13. Сколькими способами из колоды в 36 листов можно выбрать не упорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно:
- •14. Сколько различных слов можно получить перестановкой букв слова ?
- •16. Из данной пропорции найти х и y
- •17. Найти коэффициенты при xk в разложении данного выражения р по полиномиальной формуле, полученный после раскрытия скобок и приведения подобных членов.
- •18. Сколько натуральных чисел от 1до 10000 не делится ни на , ни на , ни на , ни на ?
- •19. Подсчитать количество различных перестановок цифр данного числа , при которых никакие n одинаковых цифр не идут друг за другом.
- •20. Сколько существует перестановок n различных предметов, при которых на своих первоначальных местах окажутся ровно k или ровно m предметов?
- •21. Составив таблицы истинности, выясните, равносильны ли следующие формулы алгебры высказываний:
- •22. Докажите, что следующая формула является тавтологией алгебры высказываний:
- •23. Построить таблицу данной булевой функции f(X, y, z)
- •27. Преобразовать данную формулу f(X,y,z) в эквивалентную ей, но не содержащую фиктивных переменных.
- •28. Выяснить вопрос о равносильности днф сведением их к сднф. Преобразовать с помощью дистрибутивных законов в кнф, упростить полученное выражение.
- •29. Найти двумя способами полином функции. Найти сднф, скнф.
- •30. Для функции f(x1, x2, x3, x4) минимизировать ее сднф двумя способами.
- •31. Доопределить функции f(X,y,z), g(X,y,z), h(X,y,z) так, чтобы f Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам
23. Построить таблицу данной булевой функции f(X, y, z)
|
№ |
f(x, y, z) |
№ |
f(x, y, z) |
№ |
f(x, y, z) |
|
1 |
x
+ y
Ù
z
→
|
11 |
x
Ú
y Ú
|
21 |
(x
→ y) + z «
|
|
2 |
(x│y)
→
|
12 |
(x
+ y) + (z Ú
|
22 |
(x ¯y) « z + y |
|
3 |
(x
→
|
13 |
x
Ú
y + z→ |
23 |
(x Ú y) + z → y |
|
4 |
x
Ú
y +
|
14 |
(x
¯y)
+ z Ú |
24 |
x
Ù
y + z →
|
|
5 |
x
Ú
|
15 |
(x
Ú
y → |
25 |
(x + (y ¯ z)) + y |
|
6 |
|
16 |
x
«
y + z Ú |
26 |
|
|
7 |
(x
¯y)
Ú
|
17 |
x
Ú
y Ù
|
27 |
(x│y)
+ (y → z Ù
|
|
8 |
(x Ù y → z) Ú x+y |
18 |
(x
→ |
28 |
|
|
9 |
(x│y)
Ù
→
|
19 |
(x
+ y) Ù
z Ú
|
29 |
y + z « z Ù x Ú x |
|
10 |
(x
→ y Ù
z) +
|
20 |
(x│y)
Ù
z Ú
|
30 |
x
Ù
|
24. Написать таблицу функции h(x,y), являющуюся суперпозицией функций fn и fk, если f1=(1001 0111), f2=(0110 1011), f3=(1110 0110), f4=(0111 0011), f5=(1100 0111), f6=(1001 0100), f7=(1011 0101), f8=(1000 0110), f9=(1010 0110), f10=(0101 1000).
|
№ |
n |
k |
h(x,y) |
№ |
n |
k |
h(x,y) |
№ |
n |
k |
h(x,y) |
|
1 |
1 |
2 |
fn(x, fk(x,x,y),y) |
11 |
4 |
3 |
fn(x,y, fk(y,x,y)) |
21 |
10 |
5 |
fn(fk(x,y,y),x,y) |
|
2 |
2 |
2 |
fn(x, fk(y,x,y),x) |
12 |
2 |
4 |
fn(x,fk(x,y,y),y) |
22 |
7 |
9 |
fn(fk(y,y,x),x,y) |
|
3 |
1 |
1 |
fn(y, fk(x,y,x),x) |
13 |
5 |
7 |
fn(x,y, fk(y,x,x)) |
23 |
8 |
7 |
fn(fk(x,y,y),y,x) |
|
4 |
3 |
5 |
fn(x, fk(y,x,y),y) |
14 |
9 |
8 |
fn(y,y, fk(x,y,x)) |
24 |
7 |
8 |
fn(fk(x,y,x),x,y) |
|
5 |
3 |
2 |
fn(y, fk(x,y,x),x) |
15 |
7 |
5 |
fn(x,y, fk(x,y,y)) |
25 |
6 |
7 |
fn(fk(y,x,x),y,x) |
|
6 |
4 |
3 |
fn(x, fk(y,y,x),y) |
16 |
8 |
7 |
fn(x,x, fk(y,x,y)) |
26 |
9 |
2 |
fn(x, fk(y,y,x),y) |
|
7 |
2 |
3 |
fn(x,fk(x,y,y),y) |
17 |
7 |
8 |
fn(y, fk(x,y,x),y) |
27 |
2 |
10 |
fn(x,y, fk(x,y,x)) |
|
8 |
5 |
2 |
fn(y,x, fk(x,x,y)) |
18 |
5 |
9 |
fn(x, fk(y,x,x),y) |
28 |
3 |
9 |
fn(fk(y,y,x),x,x) |
|
9 |
5 |
4 |
fn(fk(x,y,y),x,y) |
19 |
5 |
10 |
fn(y, fk(x,y,x),x) |
29 |
10 |
7 |
fn(y,x, fk(x,y,x)) |
|
10 |
3 |
2 |
fn(x,x, fk(x,y,y) |
20 |
10 |
9 |
fn(x, fk(x,x,y),y) |
30 |
8 |
3 |
fn(x, fk(y,y,x),y) |
25. По функциям f и g, заданным векторно, построить векторное представление функции h:
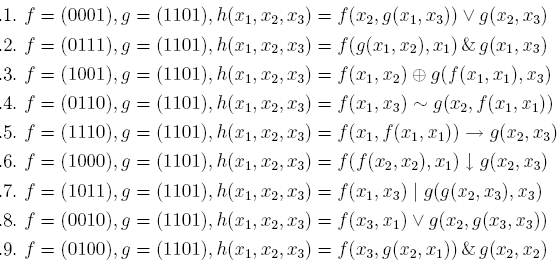

26. Для данной функции f(x,y,z) выяснить какие ее переменные являются фиктивными, а какие существенными. Выразить f(x,y,z) формулой, содержащей только существенные переменные.
|
№ |
f(x,y,z) |
№ |
f(x,y,z) |
№ |
f(x,y,z) |
№ |
f(x,y,z) |
№ |
f(x,y,z) |
|
1 |
1011 1011 |
7 |
0010 0010 |
13 |
0100 0100 |
19 |
1111 0101 |
25 |
0110 0110 |
|
2 |
0011 1100 |
8 |
1100 0011 |
14 |
1111 0011 |
20 |
0111 0111 |
26 |
1010 1111 |
|
3 |
0101 1111 |
9 |
0000 1010 |
15 |
0000 0101 |
21 |
1010 0101 |
27 |
1010 1010 |
|
4 |
1000 1000 |
10 |
1001 1001 |
16 |
0000 0011 |
22 |
0011 0011 |
28 |
1110 1110 |
|
5 |
1010 0000 |
11 |
0101 0000 |
17 |
0011 0000 |
23 |
1011 1011 |
29 |
0001 0001 |
|
6 |
1100 1111 |
12 |
1100 1100 |
18 |
1101 1101 |
24 |
1111 1100 |
30 |
0011 1111 |

 Ú
Ú

 →
x Ù
y
→
x Ù
y
 Ù
y + z
Ù
y + z )
) )
+ z Ú
x
)
+ z Ú
x
 «
y
«
y

 + y
+ y )
+ y
)
+ y Ú
y → z Ú
y
Ú
y → z Ú
y
 Ú
Ú
 +
z
+
z
 +
y
+
y )
) )
+ (z Ú
y)
)
+ (z Ú
y) Ù
(x Ú
Ù
(x Ú
 +
z)
+
z) Ú
x
Ú
x


 «
«
 +
z
+
z