
- •Тема 5 Уравнение Бернулли для элементарной струйки идеальной жидкости (струйки вязкой жидкости и для потока вязкой жидкости) Уравнение Бернулли для элементарной струйки идеальной жидкости
- •Уравнение Бернулли для потока вязкой жидкости
- •Рассмотрение энергетической и геометрической интерпретации уравнения Бернулли
- •Найдя скорости жидкости из уравнения Бернулли, легко подсчитать отношение расходов
Тема 5 Уравнение Бернулли для элементарной струйки идеальной жидкости (струйки вязкой жидкости и для потока вязкой жидкости) Уравнение Бернулли для элементарной струйки идеальной жидкости
Вспомним уравнение Эйлера для элементарной струйки идеальной жидкости:
__________________________
__________________________
___________________________
Приведем систему уравнений к виду удобному для интегрирования, для чего умножим каждое из уравнений на dx, dy, dz и почленно сложим:
(5.1)
_________________________________________________________________
Первый
трехчлен уравнения
 является полным дифференциалом
гидродинамического давления, отнесенным
к единице плотности и равен
является полным дифференциалом
гидродинамического давления, отнесенным
к единице плотности и равен :
:
 .
.

Рассмотрим движение жидкости только под действием силы тяжести, тогда внешние массовые силы, заданные в виде проекций ускорений на соответствующие координатные оси, будут X=0, Y=0, Z= -g. Тогда второй трехчлен будет равным – gdz.
Первую
часть уравнения
 преобразуем, зная, что перемещения
соответственно равны:dx
= Uxdt,
dy = Uydt,
dz = Uzdt.
преобразуем, зная, что перемещения
соответственно равны:dx
= Uxdt,
dy = Uydt,
dz = Uzdt.
Тогда:

_________________________________________________________________________
________________________________________________________________________
где U – местная скорость в сечении струйки.
Подставляя
в уравнение
 полученные значения, запишем:
полученные значения, запишем:
_____________________________ или
или 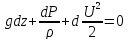 _________________________
_________________________

Если
разделить уравнение
 наg,
получим уравнение отнесенное к единице
веса:
наg,
получим уравнение отнесенное к единице
веса:
_____________________________________________________
После интегрирования получим:

____________________________________________________ 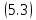
Выражение
 было получено в 1738 г. академиком Российской
Академии наук Д.Бернулли и названо
уравнением Бернулли для элементарной
струйки идеальной жидкости.
было получено в 1738 г. академиком Российской
Академии наук Д.Бернулли и названо
уравнением Бернулли для элементарной
струйки идеальной жидкости.
Уравнение Бернулли для элементарной струйки вязкой жидкости.
Для вывода уравнения Бернулли применительно к элементарной струйки вязкой жидкости рассмотрим его энергетический смысл. С этой целью подсчитаем механическую энергию бесконечно малой частицы массой dm с центром в т. А, находящейся в пределах элементарной струйки, относительно горизонтальной плоскости сравнения 01 – 01 (cм.рис.)

Как известно, потенциальная энергия равна:
______________________________________________________________
Кинетическая энергия:
_______________________________________________________
Полная механическая энергия состоит из суммы кинетической и потенциальной энергий:
________________________________________________________________________________
Отнесем энергию к единице веса жидкости, т.е. определим удельную энергию
__________________________________________________________________________
Таким образом, получим выражение, которое является уравнением Бернулли и выражает закон сохранения энергии: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии постоянная величина, т.е.
_________________________________________________________________________
Сумма

 представляет
собой потенциальную энергию, состоящую
из удельной энергии положения z и удельной
энергии давления
представляет
собой потенциальную энергию, состоящую
из удельной энергии положения z и удельной
энергии давления .
Выражение
.
Выражение называется удельной кинетической
энергией.
называется удельной кинетической
энергией.
Вдоль элементарной струйки удельные кинетическая и потенциальная энергии могут изменяться, но их сумма остается постоянной.
При движении вязкой жидкости суммарная удельная энергия движущейся жидкости вдоль струйки убывает в силу различных гидравлических сопротивлений. Следовательно, для элементарной струйки вязкой жидкости, находящейся в установившемся движении:
>
________________________________________________________________________
Чтобы получить равенство левой и правой части, необходимо в правой части добавить дополнительный член hΣ, обозначающий затрату удельной энергии на преодоление сопротивлений при движении реальной вязкой жидкости в пределах между первым и вторым сечениями. В этом случае уравнение Бернулли принимает вид:
__________________________________________________________________________
Затрачиваемая
на преодоление гидравлических
сопротивлений часть энергии превращается
из механической в тепловую, причем
необратимо. В связи с этим можно считать потерянной удельной энергией.
потерянной удельной энергией.
