1.6 Понятие линейной зависимости и линейной независимости строк (столбцов) матрицы. Теорема о ранге матрицы

Понятие ранга матрицы тесно связано с понятием линейной зависимости и линейной независимости строк (столбцов) матрицы.

В матрице рассмотрим отдельные строки.

Обозначим строки ;; …;.

Определение 1.16 Строка называется линейной комбинацией строк, если ее можно представить в виде

, где- числовые коэффициенты;

,

В этом случае, говорят, что строка линейно выражается через строки.

Определение 1.17 Система, состоящая из строк матрицы, называетсялинейно зависимой, если хотя бы одна из этих строк является линейной комбинацией других строк этой системы, например,

.

В противном случае, если ни одна из строк не может быть представлена в виде линейной комбинации других строк этой системы, строкиназываютсялинейно независимыми.

Замечание. Следует отметить, что определение 1.17 не является строгим. Строгое определение линейно зависимой и линейно независимой системы будет дано ниже.

Примеры.

1. Рассмотрим строк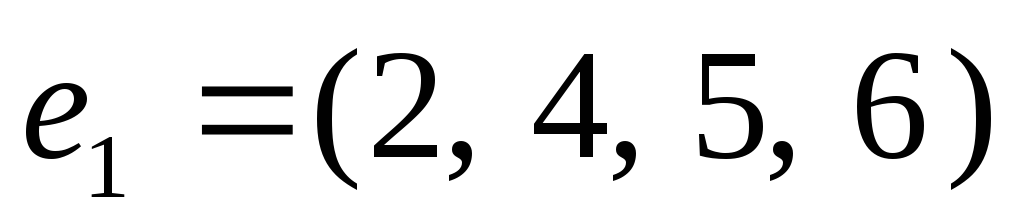и и. Нетрудно, заметить, чтот. е. строкалинейно выражается через строку, следовательно, строки- линейно зависимы.

Две пропорциональные строки – линейно зависимы.

Соответственно, две непропорциональные строки – линейно независимы.

2. Рассмотрим три строки ,,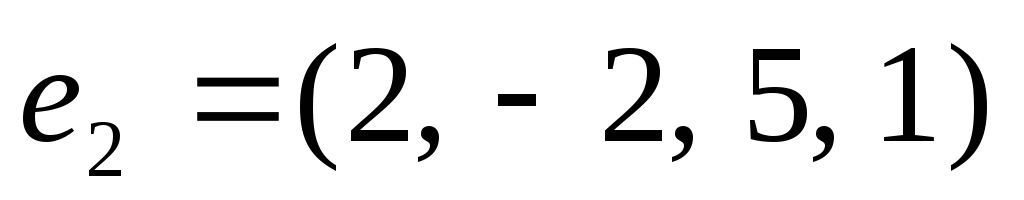Нетрудно заметить, что строкаможет быть представлена в виде суммы строки, т.е.. Следовательно, строки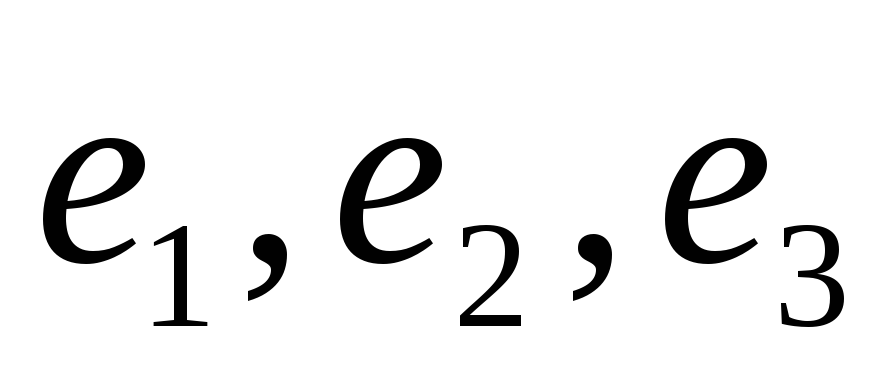- линейно зависимые.

Если отбросить строку , то строкии- линейно независимые, так как непропорциональные. Следовательно, максимальное число линейно независимых строк в данной системе равно двум.

Теорема о ранге матрицы

Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы, через которые линейно выражаются все остальные строки матрицы.

Пример.

Найти максимальное число линейно независимых строк матрицы

.

Решение.

Задача сводится к отысканию ранга матрицы . Найдем ранг матрицы, приведя ее к ступенчатому виду с помощью элементарных преобразований.

̴̴.

В ступенчатой матрице две ненулевые строки, следовательно, , а значит, максимальное число линейно независимых строк матрицы равно 2. Первая и вторая строки матрицы – линейно независимые.

Теорема о ранге матрицы имеет принципиальное значение при изучении систем линейных алгебраических уравнений.