Тема 1. Матрицы. Определители

1. Матрицы и их виды

Определение 1.1 Матрицейразмера называется прямоугольная таблица чисел, состоящая изmстрок иnстолбцов. Число в соответствующей позиции называется элементом матрицы.

В общем виде матрица записывается:

- матрица размера ,

или коротко ,;

– элемент матрицы, стоящий в– той строке и– том столбце.

Пример.

- матрица размера. Элемент.

- матрица размера. Элемент.

Матрица характеризуется:

1) размером,

2) элементами.

Определение 1.2 Две матрицы одного размера называютсяравными, если все их соответствующие элементы равны.

Пусть даны матрицы иодного размера.

Тогда , если=, где,.

Пример.

1) , 2)., так как размеры матриц не совпадают.

3) ., так как.

Виды матриц

Название	Пример	Размер	Элементы
1. Прямоугольная	,		–
2. Квадратная	,		–
3. Матрица - столбец	,		–
4. Матрица - строка	,		–
5. Нулевая матрица	,	или	,.
6. Единичная матрица	,
7. Диагональная матрица	,		Элементы образуют главную диагональ
8. Треугольная матрица (верхняя)	,

1.2 Операции над матрицами

Определение 1.3 Суммойдвух матриц размераназывается матрица того же размера, каждый элемент которой есть сумма соответствующих элементов слагаемых матриц, т.е.

,,

где ,,.

Пример.

Сложение матриц производится поэлементно.

Определение 1.4 Разностью двух матриц размера называется матрица , каждый элемент которой есть разность соответствующих элементов двух матриц т.е.

,

где

Пример.

.

Определение 1.5. Произведениемматрицы на число называется матрица того же размера, каждый элемент которой является произведением соответствующего элемента исходной матрицы на это число, т.е.

,.

Пример. .

Умножение матрицы на число производится поэлементно.

Матрица называетсяпротивоположной матрице A.

Операции сложения матриц и умножения матрицы на число называются линейными операциями над матрицами.

Свойства линейных операций над матрицами

Пусть A,B,C– матрицы,и β – действительные числа.

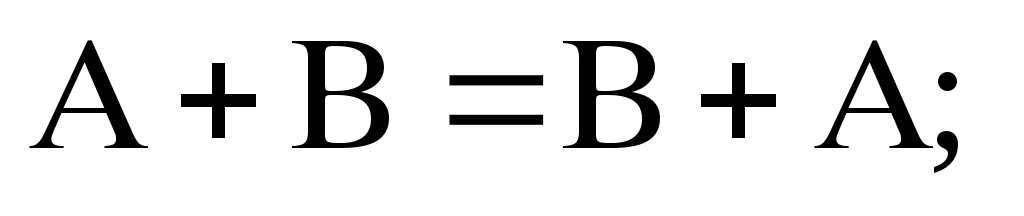
1) Коммутативность сложения	5)
2) Ассоциативность сложения	6)
3) Дистрибутивность относительно суммы матриц	7)
4) Дистрибутивность относительно суммы чисел	8)

Определение 1.6 Произведением двух матриц, первая из которых имеет размер, а втораяназывается матрица размером, каждый элемент которой, стоящий в позицииявляется суммой произведений элементовтой строки 1-го сомножителя и соответствующих элементовj-того столбца 2-го множителя. (Правило: строка на столбец).

где

Пример.

1) ,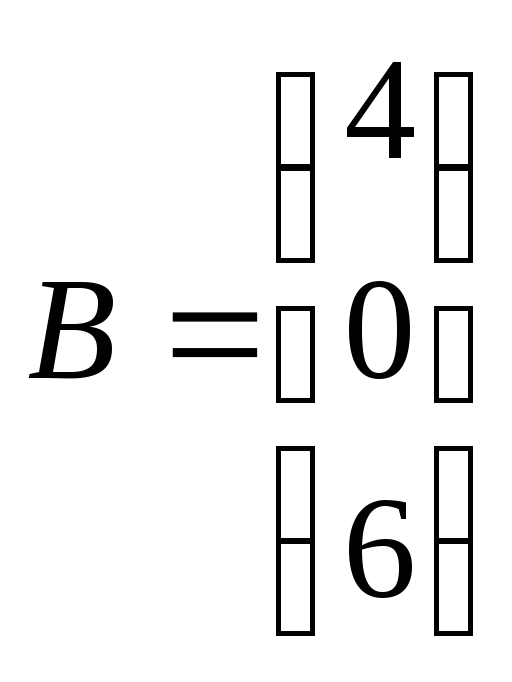.матрица-столбец

2) ;- умножение невозможно, из-за несоответствия размеров матриц.

3) Найти

4) Найти и.

,

;

Таким образом, получили, что .

Умножение матриц не обладает свойством коммутативности, т.е. в общем случае.

Две матрицы А и В, для которых выполняется равенствоназываютсякоммутативными.

Легко показать, что где А – квадратная матрица, Е – единичная матрица того же размера.

Если для заданных матриц операция умножения определена, то справедливы следующие свойства:

1) 2) или 3)

Определение 1.7 Матрица называетсятранспонированной по отношению к данной, если ее строки являются столбцами данной матрицы, т.е.

,.

Пример.

,.