2.4 Однородные системы линейных алгебраических уравнений

Линейная система называется однородной, если все ее свободные члены равны 0.

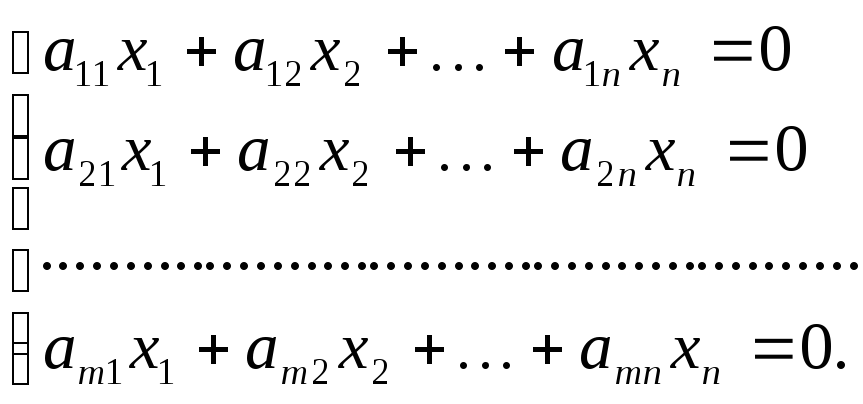(2)

В матричном виде однородная система записывается: .

Однородная система (2) всегда совместна. Очевидно, что набор чисел,, …,удовлетворяет каждому уравнению системы. Решениеназываетсянулевым илитривиальнымрешением. Таким образом, однородная система всегда имеет нулевое решение.

При каких условиях однородная система (2) будет иметь ненулевые (нетривиальные) решения?

Теорема 1.3 Однородная система (2)имеет ненулевые решениятогда и только тогда, когда рангrее основной матрицыменьше числа неизвестныхn.

Система (2) – неопределенная .

Следствие 1. Если число уравненийm однородной системы меньше числа переменных, то система является неопределенной и имеет множество ненулевых решений.

Следствие 2. Квадратная однородная системаимеет ненулевые решения тогда и тогда, когда основная матрица этой системывырождена, т.е. определитель.

В противном случае, если определитель , квадратная однородная система имеетединственноенулевое решение.

Пусть ранг системы (2) т. е система (2) имеет нетривиальные решения.

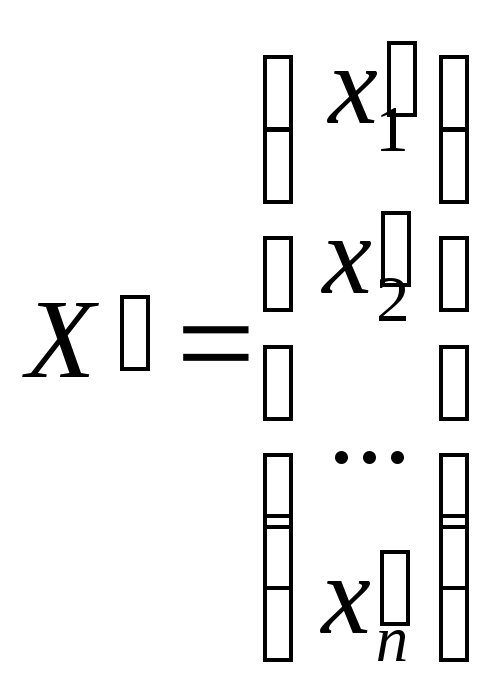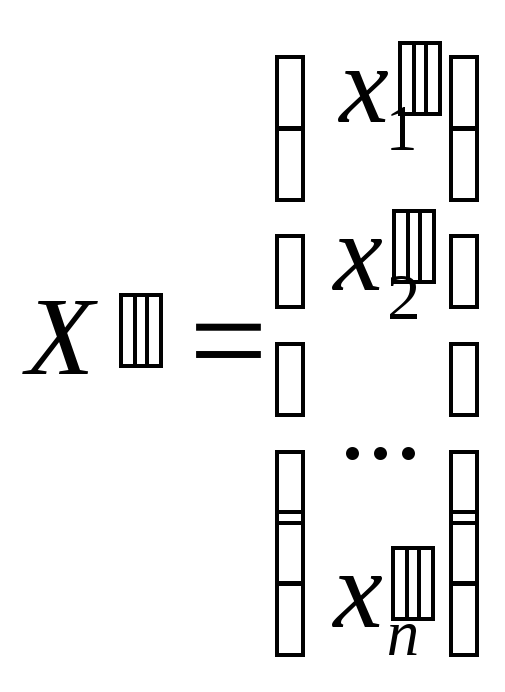Пусть и- частные решения этой системы, т.е.и.

Свойства решений однородной системы

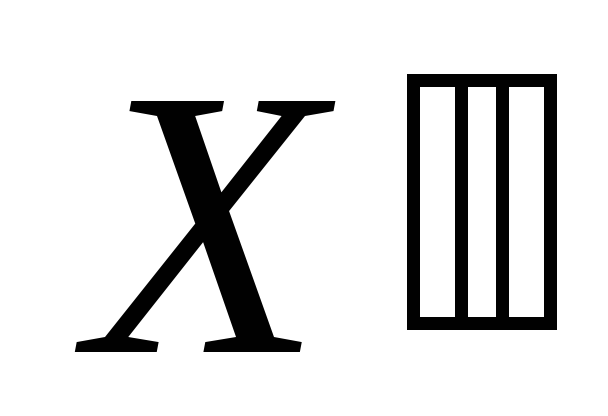1. Если и- решения однородной системы, то их сумма (+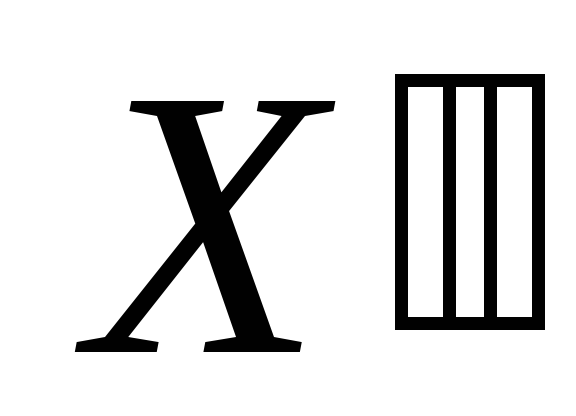) также является решением данной системы.

Действительно, .

2. Если - решение однородной системы, то при умножении его на произвольное числотакже получим решение этой системы, т.е.- решение системы.

Действительно, .

Объединяя, свойства 1) и 2), можно сказать, что если …,- решения однородной системы (2), то и всякая их линейная комбинация- также является ее решением. Здесь- произвольные действительные числа.

Можно найти линейно независимых частных решенийоднородной системы (2), с помощью которых можно получить любое другое частное решение данной системы, т.е. получить общее решение системы (2).

Определение 2.2 Совокупностьлинейно независимых частных решений…,однородной системы (2) таких, что каждое решение системы (2) можно представить в виде их линейной комбинации, называетсяфундаментальной системой решений (ФСР) однородной системы (2).

Пусть …,- фундаментальная система решений, тогда общее решение однородной системы (2) можно представить в виде:

, где.

Замечание. Чтобы получить ФСР, нужно найти частные решения…,, придавая поочередно какой-либо одной свободной переменной значение «1», а всем остальным свободным переменным – значения «0».

Получим ,, …,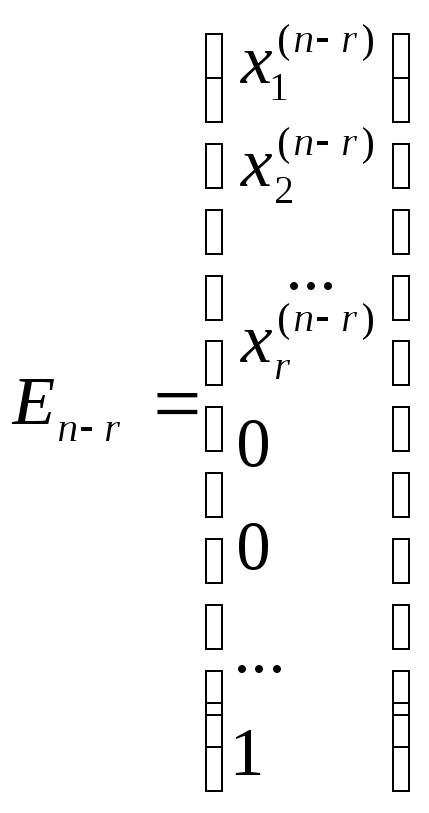- ФСР.

Пример. Найти общее решение и фундаментальную систему решений однородной системы уравнений:

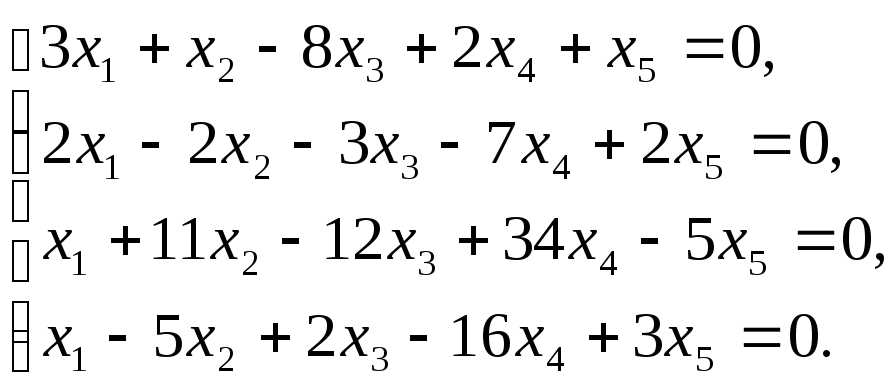
Решение. Запишем расширенную матрицу системы, предварительно поставив на первое место последнее уравнение системы, и приведем ее к ступенчатому виду. Поскольку правые части уравнений в результате элементарных преобразований не меняются, оставаясь нулями, столбец

можно не выписывать.

̴̴̴

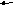
Ранг системы где- число переменных. Система неопределенная, имеет множество решений.

Базисный минор при переменных отличен от нуля:выбираемв качестве базисных переменных, остальные- свободные переменные (принимают любые действительные значения).

Последней в цепочке матрице соответствует ступенчатая система уравнений:

(3)

Выразим базисные переменные через свободные переменные(обратный ход метода Гаусса).

Из последнего уравнения выразим :и подставим в первое уравнение. Получим. Раскроем скобки, приведем подобные и выразим:.

Полагая ,,, где, запишем

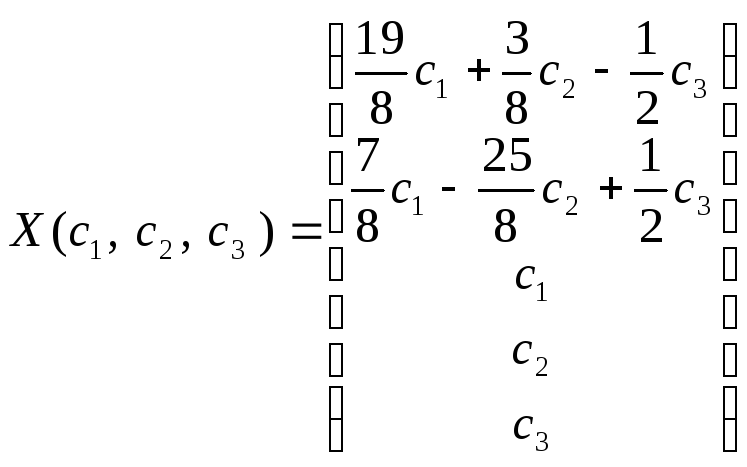- общее решение системы.

Найдем фундаментальную систему решений

,,.

Тогда общее решение однородной системы можно записать в виде:

.

Замечание. ФСР можно было найти другим путем, без предварительного отыскания общего решения системы. Для этого полученную ступенчатую систему (3) нужно было решить трижды, полагая для:; для:; для:.