Глава 6. Устойчивость линейных систем автоматического управления
6.1. Понятия и условия устойчивости
При проектировании системы управления ключевой проблемой является обеспечение её устойчивости, т.к. устойчивость является важнейшей характеристикой любой САР. С практической точки зрения неустойчивая система не имеет никакого смысла, т.к. только устойчивая система работоспособна.
Любая система управления испытывает внешние воздействия. Эти воздействия имеют различный характер и природу (задающие, возмущающие…). Всякие воздействия стремятся вывести систему из исходного состояния равновесия. Устойчивая система при этом переходит в новое устойчивое состояние равновесия.
Следовательно, под устойчивостью можно понимать свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
Замкнутая САР из-за наличия обратных связей склонна к неустойчивой работе. В процессе регулирования часть энергии с выхода передаётся на вход группы звеньев системы, среди которых могут быть и колебательные звенья. При работе системы в этом случае могут возникнуть колебания регулируемой величины и её отклонение от заданного значения. Наличие главной обратной связи будет способствовать поддержанию колебательного процесса и при больших коэффициентах усиления. Если параметры системы не обеспечивают необходимого затухания (рассеивания) энергии колебаний, то это может привести к неустойчивой работе, характеризуемой возрастанием амплитуды колебаний.
В устойчивых системах энергия колебаний с течением времени уменьшается, стремясь рассеяться в виде тепловой энергии, а колебания регулируемой величины, возникшие в результате возмущения, затухают. Следовательно, в результате возмущающих воздействий и следующих за ними регулирующих воздействий регулятора, в системе возникают переходные процессы.
При этом могут иметь место три вида переходных процессов.
Сходящийся переходный процесс, когда регулируемая величина, отклонившись под действием возмущающих воздействий от заданного значения, с течением времени под воздействием регулятора возвращается к заданному значению. Система, имеющая такой переходный процесс, будет называться устойчивой.
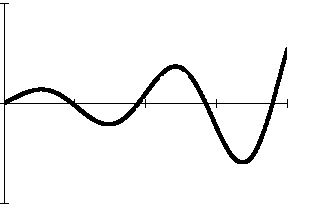
Расходящийся переходный процесс (рис. 6.1., б), когда регулируемая величина, отклонившись под действием возмущающих воздействий от заданного значения, с течением времени беспредельно удаляется от заданного значения. Этот процесс может быть апериодическим (кривая 1), или колебательным (кривая 2). Система, имеющая такой переходный процесс, будет неустойчивой.
