7.6. Последовательные корректирующие устройства

Последовательными называются корректирующие устройства, включаемые в главный контур системы регулирования последовательно с остальными звеньями системы.

Наибольшее применение получили следующие последовательные корректирующие звенья:

1. Пропорционально - дифференцирующие;

2. Пропорционально - интегрирующие;

3. Пропорционально - интегрально - дифференцирующие.

В качестве таких последовательных корректирующих звеньев могут быть использованы в контурах регулирования в системах подчиненного регулирования с последовательной коррекцией.

Последовательные корректирующие звенья служат для преобразования сигналов, пропорциональных отклонению регулируемой величины т.о., что на выходе корректирующего устройства получается сигнал, пропорциональный отклонению регулируемой величины, а также сигналы, пропорциональные производным и интегралам от отклонения.

1. Идеальное пропорционально – дифференциальное звено

Реальное дифференцирующее звено

Рассмотрим влияние дифференцирующего звена на качество переходных процессов системы, состоящей из последовательного соединения этого звена с инерционным звеном

где

Если , то инерционность апериодического звена будет скомпенсирована и в результате получим идеальное безынерционное звено с передаточной функцией.

Наиболее часто на практике применяют корректирующее устройство (регулятор) с передаточными характеристиками:

пропорционально – интегральное звено.

ПИД – звено.

В настоящее время в САУ в качестве корректирующих звеньев применяют регуляторы, включаемые в контур регулирования в системах, построенных по принципу подчиненного регулирования. Принцип построения и расчета таких систем рассмотрены в главе 8.

Глава 8. Оптимальные линейные сар

8.1. Общие сведения. Критерии качества систем регулирования

Обычно в системах автоматического регулирования параметры и свойства объекта регулирования известны. В этом случае задачей регулирующих устройств является такой выбор и настройка их параметров, при которых формируемое в этих устройствах управляющее воздействие обеспечивает изменение регулируемой величины, следующей за изменением заданного воздействия с наибольшей точностью, с наименьшей инерцией, без возникновения колебаний и независимо от изменения внешних возмущений. Идеальным регулированием является такое регулирование, когда для любого момента времени выходная координата равняется его заданному значению(рис.8.1), т.е.

.

Р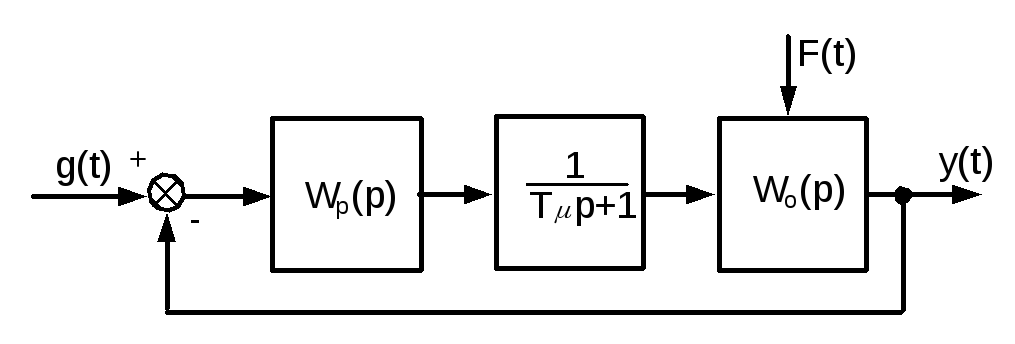ис. 8.1 Структурная схема одноконтурной САР

Однако, достигнуть этого затруднительно из-за различных ограничений в объекте регулирования и САР. Например, в реальных электроприводах ограничиваются напряжение преобразователя, его ток, ограничиваются момент и ток двигателей и т.д. Поэтому настройка контуров регулирования и всей системы в целом должна наилучшим образом отвечать поставленным требованиям.

Так, для многих технических САР, например, для электроприводов ряда механизмов, работающих в повторно-кратковременных режимах, предъявляются требования – малое время переходных процессов. В этом случае необходимо выбирать такую систему управления, параметры которой обеспечивают оптимальные по быстродействию переходные процессы с допустимыми значениями перерегулирования и колебательности. Кроме того, к динамике системы предъявляется ряд других требований, обусловленных изменением внешних условий.

Обычно для технических систем регулирования под оптимальным переходным процессом понимают такой процесс, при котором величина перерегулирования не превышала бы заданного значения, а время регулирования, а значитибыло минимально - возможным для данной системы. Кроме того, к системам регулирования предъявляется также требование– обеспечение необходимой точности регулирования в статических и динамических режимах.

Препятствием для достижения идеального поведения систем регулирования являются инерционности объекта регулирования, обусловленные всеми его звеньями, в том числе и колебательными. Поэтому возникает задача – разработать и применить для данного объекта регулирования регулятор наиболее подходящего типа и наилучшими переходными характеристиками с тем, чтобы ликвидировать влияние инерции объекта настолько полно, насколько это окажется возможным. Известно, что показатели переходного процесса зависят от количества и соотношения постоянных времен системы. Оптимальному переходному процессу соответствует оптимальное соотношение постоянных времени, что определяет соответствующие оптимальные передаточные функции и структурные схемы системы.