
- •Теория автоматического управления
- •Глава 1. Общие сведения о системах автоматического управления и регулирования
- •Основные понятия и виды автоматического управления
- •Основные принципы управления
- •Виды воздействий в системах автоматического регулирования
- •3. Импульсное воздействие
- •1.3. Классификация систем автоматического управления
- •Понятие о линейных и нелинейных системах
- •Классификация сар в зависимости от способов их настройки
- •1.4. Контрольные вопросы для самопроверки
- •Математическое описание линейных систем автоматического управления
- •2.1. Постановка задачи
- •2.2. Математическое описание линейных сау
- •Разрешив это уравнение относительно , получим статическую характеристику системы.
- •2.3. Передаточные функции сау
- •Решение:
- •2.4. Переходные функции (временные характеристики) элементов сау
- •2.5. Импульсная переходная (весовая) функция звена
- •2.6. Частотные характеристики сау
- •2.7. Логарифмические частотные характеристики сар
- •Контрольные вопросы для самопроверки
- •Глава 3. Типовые звенья систем автоматического управления
- •3.1. Разделение сау на типовые звенья
- •3.2. Безынерционное звено
- •3.3. Апериодическое звено первого порядка
- •3.4. Колебательное звено
- •А Рис. 3.10. Импульсная весовая функцияколебательного звена мплитудно-фазовая частотная характеристика колебательного звена
- •Логарифмические частотные характеристики колебательного звена
- •3.5. Апериодическое (инерционное) звено второго порядка
- •Временные характеристики звена
- •Частотные характеристики звена
- •3.6. Консервативное звено
- •Частотные характеристики звена
- •3.7. Интегрирующие звенья
- •Идеальное интегрирующее звено
- •Переходная функция интегрирующего звена
- •Частотные характеристики интегрирующего звена
- •Реальные интегрирующие звенья или интегрирующие звенья с замедлением
- •Логарифмические частотные характеристики
- •Временные характеристики
- •Частотные характеристики звена
- •3.10. Пропорционально-дифференцирующее звено
- •Частотные характеристики пд – звена
- •Глава 4. Структурные схемы сар и их преобразования
- •Понятия о структурной схеме
- •4.2. Пример составления структурной схемы системы
- •4.3. Получение передаточной функции разомкнутой системы по передаточным функциям звеньев
- •4.3.1. Передаточная функция цепи последовательно соединенных звеньев направленного действия
- •4.3.2. Параллельное соединение звеньев направленного действия
- •4.3.3. Передаточная функция системы, охваченной обратной связью
- •4.4. Преобразование структурных схем
- •4.5. Построение частотных характеристик разомкнутой системы по частотным характеристикам звеньев
- •4.6. Построение логарифмических частотных характеристик
- •4.7. Передаточные функции замкнутых cap
- •4.7.1. Передаточные функции замкнутой системы по отношению к задающему и возмущающему воздействиям
- •Передаточная функция системы по ошибке
- •4.8. Контрольные вопросы
4.2. Пример составления структурной схемы системы
В качестве примера рассмотрим составление структурной схемы двигателя постоянного тока независимого возбуждения, как объекта регулирования. Электрическая схема двигателя представлена на рис. 4.3.

Представим основные уравнения для двигателя независимого возбуждения, полагая, что магнитный поток двигателя Ф = const :
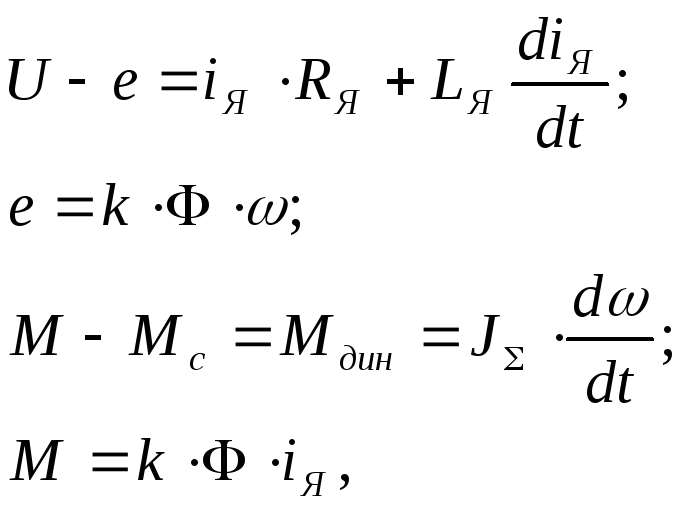
 (4.1)
(4.1)
где
![]() ,
,![]() – соответственно напряжение и ЭДС
двигателя;
– соответственно напряжение и ЭДС
двигателя;
![]() ,
,
![]() –
ток якоря и момент двигателя;
–
ток якоря и момент двигателя;
![]() ,
,![]() – активное сопротивление и индуктивность
обмотки якоря двигателя.
– активное сопротивление и индуктивность
обмотки якоря двигателя.
Запишем уравнения (4.1) в операторном виде
 (4.2)
(4.2)
Для якорной цепи как динамического звена можно получить следующую передаточную функцию
![]() (4.3)
(4.3)
позволяющую получить структурную схему звена:

А налогично
можно представить структурные схемы
других звеньев по их передаточным
функциям
налогично
можно представить структурные схемы
других звеньев по их передаточным
функциям
![]() (4.4)
(4.4)
![]()

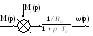 (4.5)
(4.5)
 (4.6)
(4.6)
По структурным схемам отдельных звеньев может быть получена полная структурная схема двигателя независимого возбуждения, как объекта регулирования (рис. 4.5.).

4.3. Получение передаточной функции разомкнутой системы по передаточным функциям звеньев
Дифференциальное уравнение всей системы может быть получено из уравнений отдельных звеньев, если исключить из них обычным порядком все промежуточные переменные и оставить только входное воздействие и выходную переменную. Но значительно более просто можно получить описание системы, если оперировать передаточными функциями звеньев.
Различают следующие способы соединения звеньев:
п
( 4.7)
(4.8)
(4.9)
(4.10)
(4.11)
оследовательное, при котором выходная величина предыдущего звена является входной для последующего звена;параллельное, при котором на вход нескольких звеньев подается одна и та же величина, а выходная величина представляет собой сумму выходных величин этих звеньев;
замыкание системы или нескольких звеньев обратной связью, когда на вход замыкаемых звеньев с их выхода подается сигнал через замыкающие звенья, находящиеся в цепи обратной связи.
4.3.1. Передаточная функция цепи последовательно соединенных звеньев направленного действия
Предположим, что система состоит из n–последовательно включенных звеньев. В этом случаи можно записать следующую систему уравнений для них:
![]()
![]() (4.7)
(4.7)
………………………...
![]()
Из уравнений следует, что выходная величина первого звена является входной величиной второго звена и т.д.
Для
того, чтобы выразить зависимость между
выходной величиной системы ![]() и входной величиной
и входной величиной ![]() ,
нужно исключить все промежуточные
переменные
,
нужно исключить все промежуточные
переменные ![]() ,
,
![]() и т.д. Для этого первое уравнение нужно
подставить во второе, затем полученное
уравнение подставить в третье и т.д.
и т.д. Для этого первое уравнение нужно
подставить во второе, затем полученное
уравнение подставить в третье и т.д.
После исключения промежуточных переменных получим:
![]()
где
![]()
![]() .
.
Действительно
![]()
![]()
Следовательно, передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций звеньев. Отсюда следует, что такую цепь можно заменить в структурной схеме одним эквивалентным звеном с передаточной функцией W(p).
4.3.2. Параллельное соединение звеньев направленного действия
Д ля
параллельного включения звеньев можно
записать следующую систему уравнений
ля
параллельного включения звеньев можно
записать следующую систему уравнений
![]()
![]()
…………………………………
(4.12) (4.13) (4.14) (4.15)![]()
Следовательно, входной величиной всех параллельно соединенных звеньев является одна и та же величина Хвх. Выходная величина для каждого звена различны, они зависят от динамических свойств звеньев, а значит, от вида передаточных функций. Общая выходная величина всей системы Хвых представляет собой алгебраическую сумму выходных величин отдельных звеньев.
![]()
Сложив левые и правые части уравнения (4.12), получим
![]()
отсюда
![]()
или
![]()
![]()
Следовательно, передаточная функция группы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.
