3.10. Пропорционально-дифференцирующее звено
Это звено называют также инерционно - форсирующим. Оно описывается дифференциальным уравнением первого порядка:
В зависимости от соотношения постоянных времени T1 и T2 ПД – звено может быть:
а) дифференцирующего типа при T1>T2;
б) интегрирующего типа при T1<T2.
Операторное уравнение:
Передаточная функция звена:
(3.89) (3.90) (3.91) (3.92) (3.93) (3.94)
Графическое изображение звена:
Переходная функция звена определяется:
Характеристическое уравнение звена
позволяет
найти его корень
Переходная функция приобретает вид:
Весовая функция звена:
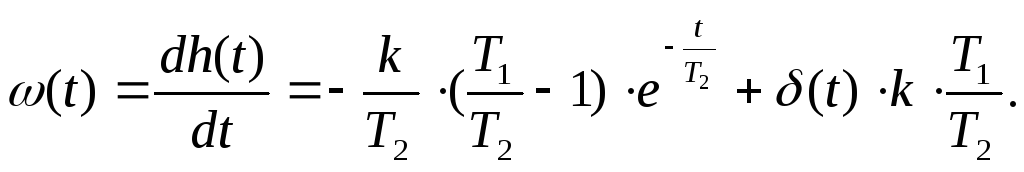
Кривые переходных функций ПД – звена двух типов представлены на рис. 3.39.
Частотные характеристики пд – звена
АФЧХ:
АЧХ:
ФЧХ:
Графическое изображение характеристик представлено на рис. 3.40.
Логарифмические частотные характеристики
3.11. Пропорционально–интегрально–дифференциальное звено (ПИД–звено)
Д
(3.95) (3.96) (3.97) (3.98)
ПИД – звено часто используется в качестве регуляторов в САР электроприводов.
Операторное уравнение звена
Передаточная функция ПИД–звена
Временные характеристики
Порядок числителя передаточной функции W(p) больше порядка знаменателя. В этом случае переходную функцию целесообразно искать в виде суммы переходных функций h(t) составляющих звеньев (рис. 3.42.).
(3.99) (3.100) (3.101) (3.102) (3.103)
Частотные характеристики
АФХ:
АЧХ:
ФЧХ:
ЛАХ:
Логарифмические частотные характеристики представлены на рис. 3.43.
Рис.
3.43. Логарифмические частотные
характеристики ПИД - звена
3.12. Запаздывающее звено
Запаздывающее
звено – это звено, которое на выходе
воспроизводит входной сигнал без
искажений, однако с некоторым постоянным
запаздыванием
.
(3.104) (3.105) (3.106) (3.107) (3.108)
У
Рис.
3.44.
Уравнение в операторном виде
Передаточная функция
Амплитудно-фазовая характеристика
Рис.
3.45. Частотные характеристики
запаздывающего звена
Графически АФХ может быть представлена окружностью с центром в начале координат с радиусом, равным k.
Логарифмическая амплитудная частотная характеристика
т.е.
совпадает с осью абсцисс.
Глава 4. Структурные схемы сар и их преобразования
Понятия о структурной схеме
В результате разбиения САУ на звенья направленного действия и получения математического описания звеньев в виде передаточных функций, частотных или переходных характеристик составляется схема системы. Эта схема может состоять из отдельных, определенным образом связанных между собой звеньев, динамические свойства которых определяются соответствующими передаточными функциями. Такая схема по существу является математической структурой реальной физической системы и называется структурной схемой. Динамические звенья, входящие в ее состав, образуют основную цепь воздействий и цепи обратных связей.
По структурной схеме можно затем получить передаточную функцию или характеристики, а также дифференциальные уравнения всей системы в целом, как в разомкнутом, так и в замкнутом состоянии.
Динамические звенья, входящие в состав структурной схемы системы соединяются между собой линиями связей, стрелки которых показывают направление действия сигнала.
Структурные схемы содержат узлы сравнения или суммирования, обозначаемые кружками с перекрещенными линиями, и точки разветвления сигнала, обозначаемые жирными точками (рис.4.2.). Линии связи, отходящие от точки разветвления, несут одни и те же сигналы.
Структурные схемы дают возможность более простым способом составить операторные уравнения и передаточную функцию системы, необходимые для исследования его динамических свойств. Использование структурных методов для получения операторного уравнения системы позволяет учесть ненулевые начальные условия cправа (при t>0) автоматически. Структурные схемы позволяют также создать общие методы исследования (анализа и синтеза) для всех систем, независимо от их конструкции, физической природы и т.д. Прежде чем составлять структурную схему необходимо разделить ее на динамические звенья, составить уравнения их динамики и получить передаточные функции звеньев.