Переходная функция интегрирующего звена

Если принять то переходная функция будет

или

(3.52)

(3.53)

Под постоянной времени интегрирующего звена понимают время, в течение которого при подаче на вход ступенчатого воздействия выходная величина достигнет этой величины.

Если входной сигнал исчезает, то выходная координата остаётся постоянной.

Весовая функция звена, т.е. реакция звена на единичный импульс имеет вид:

.

Частотные характеристики интегрирующего звена

Амплитудно-фазовая частотная функция:

. (3.54)

Т.е. амплитудно-фазовая характеристика представляет собой уравнение прямой, совпадающей с отрицательным направлением мнимой оси (рис.3.23).

(3.55)

(3.56)

(3.57)

Уравнения вещественной и мнимой частотных характеристик будут иметь вид:

Соответственно амплитудная и фазовая частотные характеристики определяются ( рис.3.25):

при ω>0;

при ω<0;

Л

(3.58)

огарифмическая амплитудная частотная характеристика:

где - прямая, параллельная оси абсцисс;

- прямая, имеющая наклон –20дб/дек и проходящая через точку на оси частот.

Следовательно, ЛАЧХ идеального интегрирующего звена представляет собой прямую, проходящую через точку с абсциссой , ординатойи имеющую наклон. Логарифмические частотные характеристики идеального интегрирующего звена представлены на рисунке 3.25.

При изменении коэффициента k L(ω) перемещается параллельно самой себе.

2. Реальные интегрирующие звенья или интегрирующие звенья с замедлением

Реальные интегрирующие звенья обычно обладают определённой инерционностью, вследствие чего, их выходная величина при подаче на вход входного сигнала изменяется с определённым замедлением.

Исходное дифференциальное уравнение интегрирующего звена с замедлением будет иметь вид:

(3.59)

(3.60)

(3.61)

(3.62)

(3.63)

или в операторном виде:

,

или

Изображение выходной величины:

Если перейти от изображения к оригиналу при подаче на вход ступенчатого воздействия и при нулевых начальных условиях, получим выражение переходной функции:

Принимая получим уравнение переходной функции, график которой приведён на рисунке. 3.26.

Импульсная весовая переходная функция, т.е. реакция звена на единичный импульс:

Передаточная функция имеет следующий вид:

.

Уравнение амплитудно-фазовой характеристики:

.

Если определить вещественную и мнимую части, то получим:

(3.64)

(3.65)

(3.66)

Амплитудная частотная характеристика:

Фазовая частотная характеристика:

Амплитудная и фазовая частотные характеристики звена представлены на рис. 3.27.

Логарифмические частотные характеристики

Логарифмическая амплитудная частотная характеристика:

(3.67)

3.8. Пропорционально–интегральное звено (изодромное)

Исходное дифференциальное уравнение звена:

и

(3.68)

(3.69)

ли

Данное звено используется обычно в качестве регуляторов электроприводов. Передаточная функция звена может быть получена:

Следовательно, рассматриваемое звено является комбинацией пропорционального и интегрирующего звеньев.

На структурных схемах ПИ­–звено изображается следующим образом.

Временные характеристики звена

Используя принцип наложения, переходная функция h(t) может быть получена как сумма переходных функций, пропорционального и интегрального звеньев, т.е.

(3.70)

(3.71)

.

Весовая функция звена

.

Для звеньев, которые содержат интегральную составляющую, при сигнале на входе равном нулю, выходной сигнал остается постоянным.

Частотные характеристики звена

АФХ (3.72)

АЧХ (3.73)

ФЧХ – аргументW(jω)

(3.74)

Л

(3.75)

огарифмические частотные характеристики

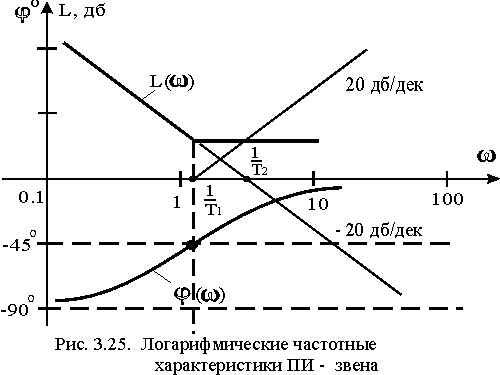
ЛАЧХ:

Рис. 3.31. Логарифмические частотные характеристики ПИ - звена

Построение ЛАЧХ следует начинать с составляющей .

Если поэтому

Если поэтому.

Наклон этой части характеристики находится следующим образом:

Следовательно, наклон характеристики составляет +20дб/дек.

Составляющая ЛАЧХ .

Если

т.е. наклон характеристики составляет –20дб/дек. ЛАЧХ и её составляющиеи, а также фазовая характеристикапредставлены на рис. 3.31.

3

(3.76)

.9. Дифференцирующие звенья

3.9.1. Идеальное дифференцирующее звено

Идеальным дифференцирующим звеном (импульсным звеном первого порядка) называется звено, выходная величина которого пропорциональна скорости изменения входной величины.

где k = T, Т – коэффициент передачи (постоянная величина), имеет размерность [c].

Примером дифференцирующих звеньев могут служить: гидравлический успокоитель с пружиной, трансформатор, цепь RC, цепь RL, и т.д. Идеальными дифференцирующими звеньями можно считать все рассмотренные выше устройства, если в них пренебречь электрическими сопротивлениями и силами трения (в механических устройствах).

Операторное уравнение звена:

Передаточная функция звена:

(3.77)

Графически дифференцирующее звено изображается следующим образом: