Министерство образования и науки Российской Федерации

Магнитогорский государственный технический университет

им. Г.И.Носова

Кафедра химической технологии неметаллических материалов

и физической химии

Изучение вязкости

ЖИДКОСТИ

Методические указания к лабораторной работе по курсу

«Процессы и аппараты химической технологии» для студентов всех форм обучения специальностей 240403, 240304 и по курсу «Введение в специальность» для специальности 200503 .

Магнитогорск

2008

Составитель В. В. Вейнский, А.В.Горохов

Изучение вязкости жидкостей: Методические указания к лабораторной работе по курсу «Процессы и аппараты химической технологии» для студентов всех форм обучения спец. 240403 и 240304 и по курсу «Введение в специальность» для спец. 200503. Магнитогорск: МГТУ, 2008. 10 с.

© Вейнский В. В.,

Горохов А.В.

Цель работы

1. Определение вязкости при различных температурах.

2. Построение зависимости вязкости каменноугольной смолы от температуры в полулогарифмическом масштабе

1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1.Общие сведения

Свойство жидких и газообразных тел оказывать сопротивление их течению – перемещению одного слоя среды относительно другого под действием внешних сил, называется внутренним трением или вязкостью. Вязкость обратна текучести (подвижности) и особенно типична для капельных жидкостей. Определяется она тепловым движением, размерами и формой молекул, их взаиморасположением («упаковкой») и действием межмолекулярных сил.

Количественная характеристика вязкости может быть рассмотрена на следующем примере. Слой жидкости толщиной h находится между двумя одинаковыми твёрдыми пластинками (рисунок 1). Нижняя пластинка А удерживается неподвижно, а верхняя В, под действием постоянной внешней касательной силы F , сдвигается параллельно нижней в направлении оси х.

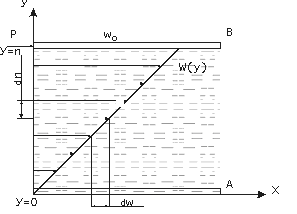
Рисунок 1 – Схема распределения сил сдвига в толщине слоя ламинарно движущейся жидкости.

Вследствие вязкого сопротивления слоя жидкости между пластинами, этот сдвиг dx₀ будет развиваться во времени t с некоторой постоянной скоростью W₀ = dx₀ / t. Разделяя весь слой жидкости на ряд тонких параллельных слоев, находим линейное распределение скоростей этих слоев по оси у : верхний слой жидкости, примыкающий к пластине В, вследствие адгезии, смещается вместе с ней, увлекая за собой нижележащий слой, движущийся с меньшей скоростью. Этот слой, в свою очередь, увлекает следующий и, с другой стороны, затормаживается им. В итоге внешняя действующая сила F, приложенная к верхнему слою, уравновешивается силой вязкого сопротивления (внутреннего трения), и течение каждого слоя проходит с постоянной во времени скоростью (установившееся течение), но убывающей линейно от слоя к слою., от наибольшей величины W₀ у пластинки В к W = 0 у неподвижной пластинки А. Такое ламинарное, т.е. послойное течение, при котором слои жидкости движутся относительно друг друга без перемешивания (в простейшем случае – однородный сдвиг, см. рисунок 1), характеризуются градиентом скорости:

G_W = dW / dy = W₀ / y₀, (1)

т.е. разности двух соседних параллельных слоев, расстояние между которыми равно единице. G_W равна скорости относительного сдвига

G_W = d / dt[ (dx₀ / y₀)], (2)

где (dx₀ / y₀) – вязкая (остаточная) деформация относительного сдвига

в слое.

Вязкость определяется по закону Ньютона (1687 год), как коэффициент пропорциональности µ (называется коэффициентом динамической вязкости) в выражении, связывающем силу F, приложенную к единице площади сдвига S (напряжение сдвига Р), с градиентом скорости:

F/S = P = µ*G_W = µ*(dW/dy). (3)

Отсюда динамическая вязкость µ = Р/G_W определяется как величина касательной силы, которая должна быть приложена к единице площади сдвигаемого слоя, чтобы поддерживать в этом слое стационарное ламинарное течение с постоянным градиентом скорости, равным единице.