группа зАЭБ-14 лектор Вострокнутова О.Н
..pdf
2014__зАЭб-14___
Контрольная работа № 1. Механика.
1. Точка движется так, что вектор её скорости V меняется со временем по закону V = 2 i + 4tj + 5t2k (м/с).
Найти модуль перемещения |
r за первые 2с её движения; модуль скорости в момент времени t=2c. |
|||||||||||
|
|
|
|
|
|
|
Ответ: |
r = 16 м; V = 21,6 м/с. |
||||
2. Твёрдое тело вращается вокруг неподвижной оси по закону |
= 20–40t+60t3(рад). Найти среднюю угловую |
|||||||||||
скорость |
как функцию от t; среднее значение углового ускорения в промежутке времени от 0 до |
|||||||||||
остановки; угловое ускорение в момент остановки. |
Ответ: |
= –40+60t2; < |
=85,1рад/с2; |
= 169,2рад/с2. |
||||||||
3. Найти ускорение, с которым движутся грузы, |
и силу натяжения нити. Масса |
|
· |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
грузов одинакова m1 = m2 = 1 кг, углы |
= 30 и |
= 45 . Коэффициент трения между |
m1 |
m2 |
||||||||
грузами и наклонными плоскостями µ = 0,1. Массой блока пренебречь. |
|
|
|
|
|
|||||||
|
|
|
|
|
Ответ: a = 0,24 м/с2; Т = 6 Н. |
|
|
|||||
|
|
|
|
|
|
|||||||
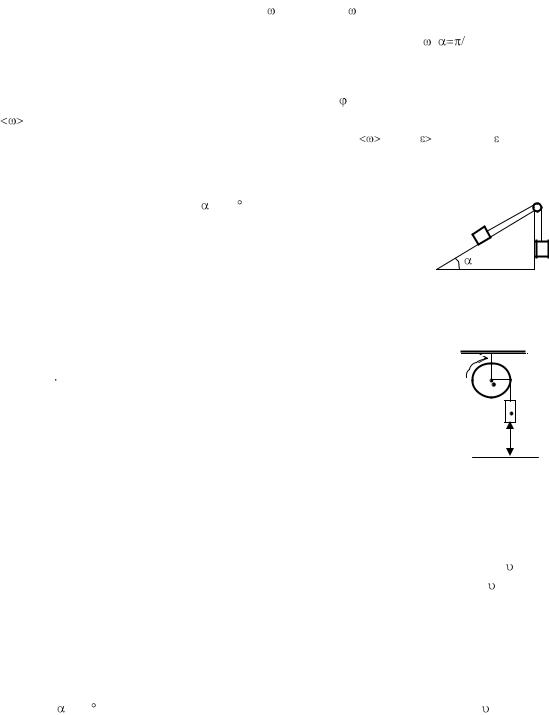
4. На гладкой наклонной плоскости, |
составляющей угол |
= 30 |
с горизонтом, |
|
|
|
|
|||||
находится катушка с ниткой, свободный конец которой укреплён, как показано на |
|
|
|
m |
||||||||
|
|
|||||||||||
рисунке. Масса катушки m = 200 г, её момент инерции относительно собственной |
|
r |
||||||||||
оси I = 0,45 г м2, радиус намотанного слоя ниток r = 3 см. Найти ускорение оси |
|
|||||||||||
|
|
|||||||||||
катушки. |
|
|
|
|
|
Ответ: а = 1,4 м/с2. |
|
|
||||
5. Шар массой m1 = 4 кг движется со скоростью |
1 = 5 м/с и сталкивается с шаром массой m2 = 6 кг, который |
|||||||||||
движется ему навстречу со скоростью |
2 = 2 м/с. Определить скорости u1 и u2 |
после абсолютно упругого |
||||||||||
удара. |
|
|
|
|
|
|
Ответ: u1 = |
3,4 м/с, u2 = 3,6 м/c. |
||||
6. Горизонтальная платформа массой m = 25 кг и радиусом R = 0,8 м вращается с частотой n1 = 18 мин 1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту
вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от I1 = 3,5 кг м2 до |
I2 |
|
= 1 кг м2. |
Ответ: n2 = 23 мин 1. |
|
Контрольная работа № 2. Электричество и магнетизм.
1. Расстояние между двумя положительными точечными зарядами q1= 9q и q 2 = q равно 8см. На каком расстоянии от первого заряда находится точка, в которой напряженность поля равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным? Ответ: 1) х = 6см; 2) х = 12см.
2. На двух коаксиальных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями 1 и 2. Найти напряженность электрического поля в точках, находящихся на расстояниях от оси цилиндров: r1=0,5R, r2=R, r3=1,5R, r4=2R, r5=3R. Построить график зависимости Е(r) для областей 1, 2, 3. Принять 1=–2 , 2= , где =50нКл/м2.
Ответ: Е1=0; Е2= –11,3кВ/м; Е3= –7,53кВ/м; Е4= –5,65кВ/м; Е5=0.
3. Конденсатор ёмкостью 10 мкФ, предварительно заряженный до напряжения U=300 B, подключили параллельно к незаряженному конденсатору ёмкостью С2=2 мкФ. Найти приращение электрической энергии этой системы к моменту установления равновесия. Объяснить полученные результаты.
Ответ: W = –0,075 Дж.
4. На рисунке 1=110 B, 2=220 В, R1= R2=100 Ом, R3=500 Ом. Найти показание амперметра. |
|
|
R2 |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сопротивлением источников и амперметра пренебречь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R3 |
|
|
|
|
|
|
|
R1 |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: I = 0,4А. |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. По двум параллельным бесконечно длинным проводникам, находящимся на расстоянии d=10 см, текут одинаковые по величине и противоположные по направлению токи I=30А. Определить индукцию магнитного поля в точке, расположенной посередине между проводниками. Ответ: В=240 мкТл.
6. Определить частоту вращения прямоугольной рамки, вращающейся в однородном магнитном поле,
магнитная индукция которого В=0,5Тл, если амплитуда наведенной в рамке ЭДС max=10В. Площадь рамки S=200см2, а число витков N=20. Ось вращения перпендикулярна вектору магнитной индукции.
Ответ: n = 8 об/с.
2014__зАЭб-14__Алкин А.Р.
Контрольная работа № 1. Механика.
1. Точка движется в плоскости XOY по закону: x=10cos t; y=10(1–sin t). Найти путь, пройденный телом за 2с; угол между векторами скорости V и ускорения a; траекторию движения у=f(x).
|
|
|
Ответ: S(2)=20 |
; |
2; x2+(10–y)2=100. |
|
2. Твёрдое тело вращается вокруг неподвижной оси по закону |
=3–t+0,1t3(рад). Найти среднюю угловую |
|||||
скорость |
как функцию от t; среднее значение углового ускорения в промежутке времени от 0 до |
|||||
остановки; угловое ускорение в момент остановки. |
Ответ: |
= 0,1t2–1; < |
= 0,55 рад/с2; |
= 1,09 рад/с2. |
||
3. Если к телу массой 25 кг приложить силу F = 120 Н под углом α = 60 к горизонту, то тело будет двигаться |
||||||
равномерно. С каким ускорением будет двигаться тело, если ту же силу приложить под углом |
β = 30 к |
|||||
горизонту? |
|
|
|
Ответ: a = 1 м/с2. |
||
4. Шар скатывается по наклонной плоскости с углом наклона 60 . Какую скорость будет иметь центр шара относительно наклонной плоскости через 2 с, если его начальная скорость была равна нулю?
Ответ: = 12,1 м/с.
5. Шар массой m1 = 4 кг движется со скоростью 1 = 5 м/с навстречу шару массой m2 = 1 кг. После центрального абсолютно неупругого удара общая скорость шаров направлена в сторону движения первого
шара и составляет |
u = 3 м/с. Определить начальную скорость второго шара и убыль механической энергии |
шаров. |
Ответ: 2 = 5 м/с; E = 40 Дж. |
6. Однородный стержень массой М = 6 кг и длиной ℓ = 2 м может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через верхний конец стержня. В нижний конец стержня
попадает пуля массой m = 10 г, летящая горизонтально со скоростью |
= 103 м/с, и застревает в нём. |
Определить кинетическую энергию стержня после удара. |
Ответ: Екин = 25 Дж. |
Контрольная работа № 2. Электричество и магнетизм.
1. Два положительных точечных заряда q и 4q закреплены на расстоянии L = 60см друг от друга. В какой точке на прямой, проходящей через заряды, следует поместить третий заряд q3 так, чтобы он находился в равновесии? Укажите, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
Ответ: между зарядами на расстоянии Х= 40см от заряда 4q; положительный.
2. Электрическое поле создано бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 1=2нКл/м² и 2=–5нКл/м². Определить напряженность поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной плоскостям. Ответ: E1 = 396 В/м; E2 = 170 В/м.
3. Три конденсатора с ёмкостями С1=2 нФ, С2=4 нФ, С3= 6 нФ соединены последовательно. Можно ли накладывать на эту батарею напряжение U=11кВ, если напряжение пробоя каждого конденсатора U =4 кВ?
Ответ: напряжение на первом конденсаторе U1= 6 кВ, поэтому нельзя.
4. ЭДС батарейки карманного фонаря 
4,5В, её внутреннее сопротивление r = 3 Ом. Сколько таких батареек нужно соединить последовательно, чтобы питать лампу, рассчитанную на напряжение U=220 В и мощность
P=60Вт? Ответ: n = 59.
5. Бесконечно длинный прямой проводник согнут под прямым углом. По |
|
|
|
|||
проводнику течет ток |
I = 20A. Какова магнитная индукция в точке А, если r |
|
|
|
||
|
|
|
||||
= 5 см? |
|
I |
|
A |
||
|
|
|||||
|
|
|
|
|
|
|
|
Ответ: В = 40 мкТл. |
|
r |
|||
|
|
|
|
|||
6. Рамка, содержащая N=200 витков тонкого провода, может вращаться вокруг оси, лежащей в плоскости рамки. Площадь рамки S=50 см2. Ось рамки перпендикулярна к линиям индукции однородного магнитного поля с индукцией В=0,005 Тл. Определить максимальную ЭДС, возникающую при вращении рамки с
частотой n = 40 Гц. Ответ: = 1,26 В
2014__зАЭб-14__Астапенко А.А.
Контрольная работа № 1. Механика.
1. Точка движется в плоскости XOY по закону: x=10cos t; y=10(1–sin t). Найти путь, пройденный телом за 10с; угол между векторами скорости V и ускорения a; траекторию движения у=f(x).
|
|
Ответ: S(10)=100 ; |
2; x2+(10–y)2=100. |
||
2. Твёрдое тело вращается вокруг неподвижной оси по закону =2t–t2(рад). |
Найти среднюю угловую |
||||
скорость |
как функцию от t; среднее значение углового ускорения в промежутке времени от 0 до |
||||
остановки; угловое ускорение в момент остановки. |
Ответ: |
= 2–t; < |
= –2рад/с2; = –2рад/с2. |
||
3. На наклонной плоскости с углом наклона |
= 30 лежит брусок массой m = 2 кг. |
· |
|
Груз массой М = 3 кг присоединён к бруску при помощи нити, перекинутой через |
m |
||
блок. Определить натяжение нити, если коэффициент трения бруска о плоскость |
|||
M |
|||
|
|
||
µ = 0,1. Массой блока и нити пренебречь. |
|
|
|
|
|
Ответ: Т = 18,7 Н. |
|
4. На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции
которого I = 0,15 кг м2, намотана легкая нить, к концу которой прикреплён груз массой R
I
m = 0,5 кг. До начала вращения барабана высота h груза над полом составила 2,3 м.
m
Определить: 1) время опускания груза до пола; 2) силу натяжения нити.
h
Ответ: t = 2 c; Т = 4,32 Н.
5. Тело массой М = 1 кг, летящее со скоростью u = 4 м/с, распадается на два осколка, масса одного из которых m = 0,6 кг. Скорость этого осколка перпендикулярна начальной скорости тела и равна 1 = 5 м/с. Чему равен модуль скорости второго осколка? Ответ: 2 = 12,5 м/с.
6. Вертикально расположенный однородный стержень массой M = 1,5 кг и длиной ℓ = 1,1 м может вращаться вокруг горизонтальной оси, проходящей через верхний конец стержня. В нижний конец стержня
попала горизонтально летевшая пуля массой m = 5 г, и застряла в нем, |
в результате чего стержень |
отклонился на угол = 45 . Определить скорость летевшей пули. |
Ответ: = 308 м/с. |
Контрольная работа № 2. Электричество и магнетизм.
1. Электрическое поле создано двумя положительными одинаковыми |
q |
1 |
q |
2 |
||||||||
точечными зарядами q. Найти работу сил поля по перемещению заряда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
|
|
a |
|
|
a |
|
|
||
q1=10нКл из точки 1 с потенциалом 1=300В в точку 2 (см. рис.). |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||||
Ответ: A= 1мкДж.
2. Бесконечно длинная тонкостенная металлическая трубка радиусом R=2см несет равномерно распределенный по поверхности заряд ( =1нКл/м²). Определить напряженность Е поля в точках, отстоящих от оси трубки на расстояниях r1=1см, r2=3см. Построить график зависимости напряженности поля от расстояния до оси трубки. Ответ: E1 = 0; E2 =75,3 В/м.
3. Плоский воздушный конденсатор, расстояние между пластинами которого d1=2 см, заряжен до разности потенциалов U=3000 В. Какова будет напряжённость поля конденсатора, если не отключая источника напряжения, пластины раздвинуть до d2=5 см? Вычислить энергию до и после раздвижения. Площадь
пластин S=100 см2. |
Ответ: W1=2 10-5 Дж, W2=0,8 10-5 Дж, E=6 104 В/м. |
||||||||||||||||||
4. В схеме на рисунке батарея, ЭДС которой равна |
120 В, сопротивления R1=25 Ом, |
|
|
– |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||
R2=R3=100 Ом. Найти мощность, выделяющуюся на сопротивлении R1. Внутренним |
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сопротивлением батареи пренебречь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: P = 16 Вт. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
||
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Бесконечно длинный тонкий проводник с током I=20 А изогнут, как показано на рис.
Определить индукцию магнитного поля в точке 0, если радиус изогнутой части 
R
0
проводника R=20 см.
Ответ: В=51,4 мкТл.
6. Изолированный металлический диск радиусом R=0,25 м вращается в перпендикулярном к диску однородном магнитном поле с индукцией В=10мТл, делая n=1000 об/мин. Найти разность потенциалов 
, возникающую между центром и краем диска. Ответ: 
33 мВ.
2014__зАЭб-14__Бояркин Э.Н.
Контрольная работа № 1. Механика.
1. Точка движется так, что вектор её скорости V меняется со временем по закону V = i + 3tj + 5t2k (м/с). Найти модуль перемещения 
r за первую 1с её движения; модуль скорости в момент времени t=1c.
Ответ: 
r = 2,45 м; V = 5,9 м/с.
2. За промежуток времени t=1c частица прошла полную окружность радиусом R = 1 м. Найти среднюю скорость движения V ; модуль средней скорости перемещения
V
; модуль среднего вектора полного ускорения 
a
, если частица двигалась из состояния покоя с постоянным тангенциальным ускорением a
.
|
Ответ: |
V =6,28 м/с; V =0 м/с; |
a =12,56м/с2. |
3. На наклонную плоскость, составляющую угол |
= 30 с горизонтом, поместили |
|
|
два соприкасающихся бруска. Массы брусков m1 = 2 кг и m2 = 3 кг, коэффициенты |
m2 |
||
трения между наклонной плоскостью и брусками |
1 = 0,2 и |
2 = 0,1. Найти силу |
m1 |
|
|||
взаимодействия между брусками в процессе движения.
Ответ: F = 1 Н.
4. Через неподвижный блок в виде однородного сплошного цилиндра массой |
m = 0,2 кг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
перекинута |
невесомая нить, к концам которой прикреплены тела массами m1 |
= 0,35 кг и |
|
|
|
|
R |
|
|
|
|
m2 = 0,55 |
кг. Пренебрегая трением в оси блока, определить отношение |
T2/T1 сил |
|
|
|
|
|
|
|||
|
|
|
m |
|
|
|
|||||
натяжения нити. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
Ответ: T2/T1 = 1,05. |
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
5. Два пластилиновых шарика, двигавшихся со скоростями 1 = 3 м/с и 2 = 5 м/с навстречу друг другу, испытывают абсолютно неупругий удар. Чему равна скорость шариков после удара, если кинетическая энергия первого шарика до удара была в n = 1,6 раза больше, чем кинетическая энергия второго?
Ответ: u = 1,53 м/с.
6. В центре скамьи Жуковского стоит человек и держит в руках за один из концов стержень длиной L = 2,4 м и массой m = 8 кг, расположенный вертикально вдоль оси скамьи. Скамья с человеком вращается с частотой n1 = 1 с 1. C какой частотой n2 будет вращаться скамья с человеком, если он повернёт стержень в горизонтальное положение? Суммарный момент инерции человека и скамьи I = 6 кг м2.
Ответ: n2 = 0,28 с 1.
Контрольная работа № 2. Электричество и магнетизм.
1. . Шарик массой 150 мг, подвешенный на непроводящей нити, имеет заряд q1 =10·10-9Кл. На расстоянии 32см от него снизу поместили второй маленький шарик. Каким должен быть по величине его заряд, чтобы натяжение нити увеличилось в 2 раза? Ответ: q2 = 1,7·10-6Кл.
2. На металлической сфере радиусом R=10 см находится заряд q =1 нКл. Определить напряженность электрического поля: 1) на расстоянии r1=8см от центра сферы, 2) на поверхности сферы, 3) на расстоянии r3=15см от центра сферы. Построить график зависимости напряженности поля от расстояния до центра сферы. Ответ: Е1= 0; E2= 900 В/м; E3= 400 В/м.
3. Плоский конденсатор заполнен диэлектриком и на его пластины подана разность потенциалов. Его энергия составляет W=2 10-5Дж. После того, как конденсатор отключили от источника напряжения, из него вынули диэлектрик. Работа, совершенная при этом против сил электрического поля A= 7 10-5 Дж. Найти диэлектрическую проницаемость вещества, заполнявшего конденсатор. Ответ: =4,5.
4. Элемент замыкают сначала на внешнее сопротивление R1=2 Ом, а затем на внешнее сопротивление R2=0,5 Ом. Найти ЭДС элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев, мощность, выделяемая во внешней цепи, одинакова и равна P= 2,54 Вт. Ответ: r = 1 Ом, 
= 3,4 В.
5. Найти индукцию магнитного поля внутри длинного соленоида при силе тока в нем I=8 А, если на длине l=40 см намотано N=400 витков проволоки. Как изменится индукция магнитного поля, если внутри соленоида поместить железный сердечник с магнитной проницаемостью =2000?
Ответ: В0=0,01 Тл; Вс=20 Тл.
6. В магнитном поле, индукция которого B=0,05 Тл вращается стержень длиной L=1 м с постоянной угловой скоростью =20 рад/с. Ось вращения проходит через конец стержня и параллельна силовым линиям
магнитного поля. Найти ЭДС индукции, возникающей на концах стержня. Ответ: =0,5 В.
2014__зАЭб-14__Быстров Д.И.
Контрольная работа № 1. Механика.
1. Точка движется в плоскости XOY по закону: x = - 2t; y = 4t(1 – t). Найти уравнение траектории y = f(x) и
изобразить ее графически; вектор скорости v |
и ускорения a в зависимости от времени; модуль скорости в |
момент времени t = 1,2 с. |
Ответ: y=–x2–2x; v=5,95 м/с. |
2. За промежуток времени t=100c частица прошла 1/2 окружности радиусом R= 3,2 м. Найти среднюю скорость движения V ; модуль средней скорости перемещения
V
; модуль среднего вектора полного ускорения 
a
, если частица двигалась из состояния покоя с постоянным тангенциальным ускорением a
.
Ответ: V =0,1 м/с; 
V
=0,064 м/с; 
a
=2 10-3м/с2.
3. С какой наименьшей силой нужно толкать перед собой тележку, масса которой m = 12 кг, для того чтобы сдвинуть её с места? Сила направлена вдоль ручки тележки и составляет угол α = 30о с горизонтом, а коэффициент трения между полом и тележкой = 0,4? Ответ: F = 70,6 Н.
4. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2
кг. Определить момент инерции маховика, если он, вращаясь |
равноускоренно под действием силы тяжести |
груза, за время t = 3 с приобрел угловую скорость = 9 рад/с. |
Ответ: I = 1,8 кг м2. |
5. Снаряд массой m1 = 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 1 = 500 м/c, попадает в вагон с песком массой m2 = 10000 кг и застревает в нём. С какой скоростью u станет
после этого двигаться вагон, если до попадания снаряда он двигался со |
скоростью 2 = 36 км/ч в |
направлении, противоположном движению снаряда? |
Ответ: u = 17,8 км/ч. |
6. Однородный стержень длиной ℓ = 1 м и массой М = 2 кг может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец стержня ударяет пуля массой m = 10 г, летящая перпендикулярно стержню и его оси вращения, и застревает в нем. Определить угол, на который при этом отклонится стержень. Скорость пули = 300 м/с. Ответ: = 72 .
Контрольная работа № 2. Электричество и магнетизм.
1. Найти потенциалы электрического поля в точках A и B, находящихся от заряда q=1,67 нКл на расстояниях r1=5 см и r2=20см. Определить работу электрических сил при перемещении заряда q1=1 нКл из точки A в точку B.
A 
B r1 r2
q 
Ответ: 1=300 B; 2=75 B; A= 2,25 10 7 Дж.
2. Две концентрические металлические заряженные сферы радиусами R1=6 см и R2=10 см несут соответственно заряды q1=1 нКл и q2=–0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r1=5см и r2=9см. Построить график зависимости напряженности поля от расстояния до центра сферы. Ответ: Е1= 0; E2= 1,1 кВ/м.
3. Найти напряжение на зажимах цепи (см. рис.) и общую ёмкость |
|
C1 |
|
|
C4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
батареи конденсаторов, если С1=С5=4мкФ, С2=3мкФ, С3=5мкФ, |
|
|
C2 |
|
|
|
|
|
|
|
|
||
С4=2мкФ, а напряжение между точками а и в в цепи равно 100 В. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
с |
||
а |
|
|
C3 |
|
C5 |
||||||||
Ответ: UAC=300 В; C=4 мкФ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Какую силу тока показывает миллиамперметр в схеме на рисунке, если 1=2B, 2=1В, R1=1000 Ом, R2=500 Ом, R3=200 Ом и сопротивление миллиамперметра RmA=200 Ом? Внутренним сопротивлением элементов пренебречь.
Ответ: I = 0,45 мА.
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mA |
||||||
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
R3 |
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Найти индукцию магнитного поля в центре петли радиусом R=10 см, |
|
|
|
|
|
||||
образованной бесконечно длинным тонким проводником с током I=50 А (см. |
|
0 |
I |
|
|
||||
рисунок). |
Ответ: В=414 мкТл. |
|
|
|
|
|
|||
|
|
I |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
6. Тонкий металлический стержень длиной L=1,2 м вращается в однородном |
O’ |
B |
|
|
|
||||
магнитном поле вокруг оси OO’, перпендикулярной к стержню, отстоящей от |
|
|
|
|
|||||
одного из его концов на расстояние ℓ=0,25 м, делая n=120 об/мин. Вектор В |
|
|
ℓ |
|
|
|
|
||
|
|
|
|
L |
|
|
|||
параллелен оси вращения и B=1мТл. Найти разность потенциалов между |
|
|
|
|
|||||
O |
|
|
|
|
|||||
концами стержня. |
Ответ: |
5,3 мВ. |
|
|
|
|
|||
|
|
|
|
|
|||||