
- •Уравнение движения электропривода
- •Основы алгебры логики, основные операции, аксиомы и теоремы
- •Нарисовать и объяснить механические характеристики асинхронного двигателя при изменении напряжения питающей сети и при изменении величины активного сопротивления цепи ротора.
- •Переходные процессы в электроприводах постоянного тока.
- •Логические элементы «и-не» и «или-не» кмоп. Принцип работы. Достоинства и недостатки.
- •Основные характеристики синхронного двигателя
- •Нарисовать и объяснить механические характеристики электропривода с двигателем постоянного тока независимого возбуждения при изменении напряжения
- •Исполнительные двигатели в мехатронных системах и их основные характеристики
- •Технический оптимум при настройке регуляторов тока и скорости
- •Структура мехатронной системы и основное оборудование
- •Выбор двигателей по мощности для кратковременного режима работы s2
- •Система подчиненного регулирования с регулятором эдс
- •Нарисовать и объяснить скоростные характеристики асинхронного электропривода
- •Выбор двигателей по мощности для повторно-кратковременного режима работы s3.
- •Логический Элемент «или» Схема,принцип работы, достоинства и недостатки
- •Законы частотного регулирования скорости асинхронных электроприводов
- •Структурные схемы электроприводов постоянного тока
- •Тормозные режимы работы электроприводов переменного тока(только асинхронник)
- •Перегрузочная способность электроприводов
- •Особенности исполнительных элементов в мехатронных системах металлургического производства
- •Потери и расход энергии в переходных процессах электроприводов постоянного тока
-
Уравнение движения электропривода
При
поступательном движении движущая
сила F всегда
уравновешивается силой сопротивления
машины Fc и
инерционной силой: ![]() ,
возникающей при изменении скорости.
механическая мощность, развиваемая
электродвигателем, полностью расходуется
на преодоление момента сопротивления
нагрузки, т.е. на совершение работы
рабочим органом: Мд =
– М'с
Уравнение равновесия сил при поступательном
движении примет вид:
,
возникающей при изменении скорости.
механическая мощность, развиваемая
электродвигателем, полностью расходуется
на преодоление момента сопротивления
нагрузки, т.е. на совершение работы
рабочим органом: Мд =
– М'с
Уравнение равновесия сил при поступательном
движении примет вид:
![]()
где m – масса тела, Н; V – скорость, м/с,; F – сила, Н.
Аналогично
уравнение равновесия моментов для
вращательного движения, называемое основным
уравнением движения электропривода:

В
некоторых случаях принято говорить,
что развиваемый двигателем вращающий
момент Мд уравновешивается
моментом сопротивления М'с на
его валу и инерционным
или динамическим моментом: ![]() .
.
Из анализа видно:
1) при Мд > М'с – dω/dt > 0, т. е. имеет место ускорение (разбег) привода;
2) при Мд < М'с – dω/dt < 0, т. е. имеет место замедление привода (замедление привода может быть и при отрицательном значении момента двигателя);
3) при Мд = М'с – dω/dt = 0; в данном случае привод работает в установившемся (статическом) режиме.
Вращающий
момент, развиваемый двигателем при
работе, принимается положительным, если
он направлен в сторону движения привода.
Если он направлен в сторону обратную
движению, то он считается отрицательным.
В
общем виде уравнение движения привода
может быть записано следующим образом:![]()
-
Определить частоту ЭДС и тока ротора асинхронного двигателя Pном = 10кВт, Uном = 380/220В; nном = 1450 об/мин. в начальный момент пуска и при номинальной частоте вращения. Какова частота тока и ЭДС ротора при S = 1,5 ?
Частота тока статора пропорциональна частоте вращения магнитного поля, созданного током статора:
f1 = n0p/60.
Частота тока питающей сети 50Гц
Частота ЭДС и тока ротора при S=1.5; f2=f1*s=50*1.5=75Гц.
В начальный момент пуска в обмотках ротора протекает ток с частотой сети, т.е 50Гц
1. Частота вращения магнитного поля асинхронной машины, об/мин:
 ,
,
где f1 – частота тока питающей цепи;
р – число пар полюсов статорной обмотки машины.
2. Частота вращения ротора, об/мин:
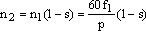 ,
,
где s – скольжение асинхронной машины.
3. Скольжение асинхронной машины:
 или
в процентах
или
в процентах  .
.
Частота ЭДС и тока, наводимых в роторе магнитным полем статора:
 .
.
|
|
-
Основы алгебры логики, основные операции, аксиомы и теоремы
В
алгебре логики рассматриваются
переменные, которые могут принимать
только два значения: 0 и 1. В дальнейшем
переменные будем обозначать латинскими
буквами х,
у, z,... . В
алгебре логики определеноотношение
эквивалентности (=)
и три операции:дизъюнкция (операция
ИЛИ), обозначаемая знаком V
(+); конъюнкция (операция
И), обозначаемая точкой, которую можно
опускать (например, х·у=ху);
отрицание(инверсия,
операция НЕ), обозначаемое чертой над
переменными или элементами 0 и 1
(например, ![]()
![]() ,
, ![]() ).
Отношение эквивалентности удовлетворяет
следующим свойствам: х
= х -рефлексивность; если х
= у, то у
= х - симметричность; если х
= у и у
= z,
то x
= z- транзитивность. Из
отношения эквивалентности следует принцип
подстановки: если х
= у, то
в любой формуле, содержащей х, вместо х можно
подставить у, и
будет получена эквивалентная формула.
).
Отношение эквивалентности удовлетворяет
следующим свойствам: х
= х -рефлексивность; если х
= у, то у
= х - симметричность; если х
= у и у
= z,
то x
= z- транзитивность. Из
отношения эквивалентности следует принцип
подстановки: если х
= у, то
в любой формуле, содержащей х, вместо х можно
подставить у, и
будет получена эквивалентная формула.
Определение
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывания
строятся над множеством {B, ![]() ,
, ![]() ,
, ![]() ,
0, 1}, где B — непустое множество, над
элементами которого определены
три операции:
,
0, 1}, где B — непустое множество, над
элементами которого определены
три операции:
![]() отрицание (унарная
операция),
отрицание (унарная
операция),
![]() конъюнкция (бинарная),
конъюнкция (бинарная),
![]() дизъюнкция (бинарная),
дизъюнкция (бинарная),
а логический ноль 0 и логическая единица 1 — константы.
Так же используются названия
-
Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например
 ).
). -
Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например
 ).
).
Унарная
операция отрицания в тексте формул
оформляется либо в виде значка перед
операндом (![]() )
либо в виде черты над операндом (
)
либо в виде черты над операндом (![]() ),
что компактнее, но в целом менее заметно.
),
что компактнее, но в целом менее заметно.
Аксиомы]
-
 , инволютивность
отрицания, закон
снятия двойного отрицания
, инволютивность
отрицания, закон
снятия двойного отрицания -

-

-

-

-
-

-

-

Логические операции[
Простейший и наиболее широко применяемый пример такой алгебраической системы строится с использованием множества B, состоящего всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать[неопределённость], что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь
на этот математический инструментарий, логика
высказываний изучает высказывания и предикаты.
Также вводятся дополнительные операции,
такие какэквиваленция ![]() («тогда
и только тогда, когда»), импликация
(«тогда
и только тогда, когда»), импликация ![]() («следовательно»),
сложение по модулю два
(«следовательно»),
сложение по модулю два ![]() («исключающее
или»), штрих
Шеффера
(«исключающее
или»), штрих
Шеффера ![]() , стрелка
Пирса
, стрелка
Пирса ![]() и
другие.
и
другие.
Логика
высказываний послужила
основным математическим инструментом
при создании компьютеров. Она легко
преобразуется в битовую логику:
истинность высказывания обозначается
одним битом (0 — ЛОЖЬ, 1 — ИСТИНА);
тогда операция ![]() приобретает
смысл вычитания из единицы;
приобретает
смысл вычитания из единицы; ![]() —
немодульного сложения; & —
умножения;
—
немодульного сложения; & —
умножения; ![]() —
равенства;
—
равенства; ![]() —
в буквальном смысле сложения по модулю
2 (исключающее Или — XOR);
—
в буквальном смысле сложения по модулю
2 (исключающее Или — XOR); ![]() —
непревосходства суммы над 1 (то есть
A
—
непревосходства суммы над 1 (то есть
A ![]() B
= (A + B) <= 1).
B
= (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено»), комплексную логику и др.
Свойства логических операций
-
Коммутативность: x
 y
= y
y
= y x,
x,  {&,
{&,  }.
}. -
Идемпотентность: x
 x
= x,
x
= x,  {&,
{&,  }.
}. -
Ассоциативность: (x
 y)
y) z
= x
z
= x (y
(y z),
z),  {&,
{&,  }.
}. -
Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
-
 ,
, -
 ,
, -
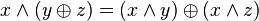 .
.
Законы де Мо́ргана:
-
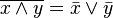 ,
, -
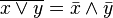 .
.
Законы поглощения:
-
 ,
, -
 .
.
Другие (1):
-
 .
. -
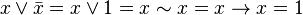 .
. -
 .
. -
 .
. -
 , инволютивность
отрицания, закон
снятия двойного отрицания.
, инволютивность
отрицания, закон
снятия двойного отрицания.
Другие (2):
-
 .
. -
 .
. -
 .
. -
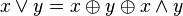 .
.
Другие (3) (Дополнение законов де Мо́ргана):
-
 .
. -
 .
.
