Поперечная сила и изгибающий момент.
В поперечных сечениях балки возникает поперечная сила Q и изгибающий моментM.
|
|
Разрежем балку на расстоянии Х. Заменим действие отброшенной части (правой) внутренними усилиями Q и M; рассмотрим левую часть балки. Q – поперечная сила - результирующая всех внутренних усилий алгебраически равна сумме всех сил, расположенных левее сечения. M – изгибающий момент результирующий момент всех внешних сил, численно равен алгебраической сумме моментов всех усилий, расположенных левее сечения. Составим уравнения равновесия для левой части:
|
→
→
∑МсечХ=0;
→
→
;
Можно вместо левой части рассмотреть правую часть. Результат будет тот же, но с обратным знаком.
В связи с этим для того, чтобы в одном и том же сечении Q и M имели одинаковые знаки независимо от того какая часть рассматривается, примем следующее
ПРАВИЛО ЗНАКОВ (см. рисунок):
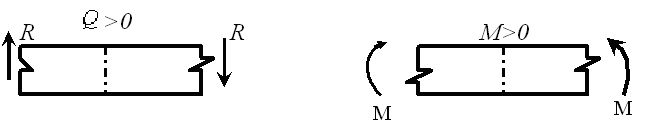
Поперечную силу будем считать положительной, если равнодействующая сила левее сечения направлена вверх, а правее сечения направлена вниз.
Изгибающий момент будет считаться положительным, если равнодействующий момент левых сил направлен по ходу часовой стрелки, а правых – против часовой стрелки.
Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
|
|
Выделим из балки участок бесконечно малой длины так чтобы по границам этого участка и по самом участке сосредоточенные силы отсутствовали.
Ввиду малости участка распределенную
нагрузку
Составим уравнения равновесия:
|
примем равномерно распределенной
.
;
или
;
;
Пренебрегая бесконечно
малыми величинами второго порядка,
получаем:
или
Продифференцировав последнее
выражение по Х,
получаем:
;или
Построение эпюр изгибающих моментов и поперечных сил.
Внутренние усилия Q и M зависят от координатыХ,поэтому удобно иметь графики зависимостиQ и M от расстоянияХ,эти графики называютсяэпюрамипоперечных сил и изгибающих моментов. Построение эпюрQ и M рассмотрим на частных примерах.
|
Положительные изгибающие моментыбудем откладывать в сторону растянутых волокон.
|
Пример 1. Построить эпюры Q иM.
1) Определяем опорные реакции:
2) Разбиваем балку на участки. Рассмотрим отдельные участки. 3) Участок 1: (рассекаем на расстоянии Х1)
Участок 2: (рассекаем на расстоянии Х2)
при
. |
;
при
Пример 2. Построить эпюры Q иM.
Определим опорные реакции:
Проверка
,
Следовательно, опорные реакции определены верно.
2) Построим эпюры QиM:
Участок I:
Участок II:
Участок III:
|
|
Идем справа налево Из подобия треугольников . находим:
|
|
|
|
