Надежность систем централизованного теплоснабжения

Системы централизованного теплоснабжения (СЦТ) являются системами энергетики и надежность их функционирования должна быть учтена в рамках энергетического комплекса.

Эффективное управление надежностью возможно в случае принятия взаимосогласованных решений на стадии проектирования и эксплуатации с диспетчерированием.

Система теплоснабжения обслуживает город и промышленные предприятия. С позиции страны она является локальной, но как система имеет свою пространственную иерархию в построении. Так, крупную систему теплоснабжения можно разделить на три иерархических уровня: верхний уровень включает источники теплоты, средний уровень представляет магистральные тепловые сети с насосными подстанциями, низший уровень состоит из распределительных тепловых сетей и вводов к потребителям теплоты. Такая иерархизация позволяет удобно и достаточно строго оценить надежность функционирования системы теплоснабжения.

Расчет надежности верхнего иерархического уровня – источников теплоты – представляет собой самостоятельную задачу о надежности энергогенерирующего источника. Так как надежность всей системы теплоснабжения определяется требуемой надежностью подачи теплоты потребителям, поэтому, следуя взаимосвязанной цепочке иерархических уровней СЦТ от потребителей к верхнему уровню, можно сделать вывод, что каждый уровень задает условия надежности своему верхнему уровню, а общая совокупность надежности всех уровней определит в конечном итоге надежность теплоснабжения потребителей.

Рис. 5.1. Принципиальная схема системы теплоснабжения от районной котельной.

ИТ – источник теплоты (районная котельная);

КА – котлоагрегаты;

НС – насосная станция;

МТС – магистральные тепловые сети;

РТС – распределительные тепловые сети;

НП – насосная подстанция;

РТП – районный тепловой пункт;

ЦТП – центральный тепловой пункт;

ИТП – индивидуальный тепловой пункт;

Стрелки:

Т – топливо;

Э – электроэнергия;

ПВ – подпиточная вода;

П – потребители теплоты;

ДГ – дымовые газы;

В – воздух.

На рис. 5.1 представлена схема теплоснабжения с источником теплоты и районной котельной. При тепловой мощности котельной 150… 350 МВт и более систему теплоснабжения имеющую только один источник теплоты – РК, следует выполнять также с тремя иерархическими уровнями и средний уровень (магистральные тепловые сети) проектировать в виде резервированных кольцевых систем. Если мощность котельной на отдельный вывод невелика (30-50 МВт), т.е. соответствует мощности РТП, тогда тепловая сеть может быть тупиковой разветвленной. Она будет соответствовать распределительной тепловой сети (нижний иерархический уровень) системы с тремя иерархическими уровнями.

Из источника теплоты (условно) выходят только подающие линии, которые образуют второй уровень – кольцевую магистральную сеть. Эта сеть представлена в однолинейном изображении. Для того, чтобы замкнуть циркуляционный контур источника теплоты, на схеме показаны два коллектора подающих и обратных линий. Вход и выход теплоносителя показан стрелками. В СЦТ главные звенья (системы подачи электрической энергии, топлива, подпиточной воды, источник теплоты, магистральные тепловые сети и распределительные сети) представляют собой единую цепь, и отказ любого звена приводит к отказу всей системы теплоснабжения или её части.

Обеспечение надежности тепловых сетей зависит от:

1. Качества элементов системы (трубопроводов, арматуры, строительных конструкций и защиты от коррозии);

2. Резервирования участков тепловых сетей;

3. Управляемости сети, обеспечиваемой принятием оптимальной схемой сети и автоматизацией СЦТ;

4. Управления надежностью (оперативного и качественного обслуживания сетей).

5.1. Оценка надежности трубопроводов и задвижек

Тепловые сети состоят из следующих элементов: участков теплопроводов, секционирующих и отсекающих задвижек, оборудования сетей (компенсаторы, опоры, спускные краны и пр.), насосных подстанций.

Рассмотрим работу элемента с позиций теории надежности. Различают последовательное и параллельное соединение элементов.

При последовательном соединении элементов отказ любого элемента приводит к отказу всей системы.

где P – безотказность (0-1).

.

В параллельной системе соединений отказ системы происходит при отказе всех элементов

.

Интенсивность отказов l – число отказов n-элементов в системе в единицу времени, отнесенное к среднему числу элементов N, работающих в момент времени τ.

Элемент работает до отказа. После отказа его выключают из системы, ремонтируют (заменяют) и вновь включают в работу. В любой момент времени t элемент может находится в состоянии исправности либо в состоянии отказа.

Последовательность отказов элемента во времени составляет поток отказов. Поток отказов характеризуется параметром потока отказов ω, который является аналогом аналогом интенсивности отказов.

Рассмотрим основные характеристики ремонтируемых изделий. Если за год элемент отказал К раз, то поток отказов составляет К, 1/год.

При ω = const вероятность безотказной работы элемента за время t описывается дифференциальным уравнением теории массового обслуживания.

для момента времени t = 0 , элемент работоспособен.

Вероятность безотказной работы элемента за время t выражается зависимостью

Таким образом, функция надежности работы элемента подчиняется экспоненциальному закону.

Вероятность отказа элемента за время t (ненадежность) является остаточной величиной дополнения надежности до единицы

,

где ω – параметр потока отказов;

t – время работы элемента, лет.

Для линейных элементов имеет размерность (год·км)^-1; для сосредоточенных ω – (год^-1).

Величину обратную параметру потока отказов или измеряемую в годах (часах) называют наработкой на отказ. Т – это среднее время работы элемента до отказа.

Показатель степени - количеству отказов элемента за время t.

В связи с тем, что элементы системы независимы, в смысле надежности, то вероятность безотказной работы системы равна произведению вероятностей её элементов

,

где - надежность функционирования элемента i;

n – количество независимых по надежности элементов в системе:

,

где – параметр потока отказов системы:

Вероятность отказа системы (ненадежность) определяется выражением

Вероятность совмещения событий равна произведению их вероятностей, т.е. вероятности отказа двух элементов:

первого и представляет двойной отказ являющийся неординарным событием. Двойной отказ происходит в период предшествующий или последующий событию.

Вероятность свершения неординарного двойного отказа равна их произведению вероятностей

Для неординарных m отказов из n элементов (установленных насосов) вероятность свершения событий выражается произведением их вероятностей

- биноминальный коэффициент Бернулли.

Для ординарных событий вероятность свершения m ординарных отказов элементов за время t из n элементов определяется по формуле биноминального распределения

Эта формула получена из предыдущей при равенстве вероятностей всех свершающихся событий.

Учитывая существующую статистику повреждений , будем использовать средние статистические данные и считать ω постоянной величиной.

Статистическая обработка надежности элементов системы теплоснабжения

Для получения параметров потока отказов необходима статистическая информация отказа элементов по объектам. Рассматриваемыми элементами по надежности являются: трубопроводы, задвижки, обратные клапана, электродвигатели, насосы, насосные блоки и другие, а объектами - районы теплоснабжения, насосные станции, котельные.

Так для статистической обработки надежности трубопроводов исходной информацией являются матрица случайного отказа трубопроводов по объектам (районам теплоснабжения).

,

где d – диаметр трубопровода, м;

l – сумма длин участков (прямой и обратной линии) трубопроводов диаметра d;

k – число отказа трубопровода диаметром d за время _Δt;

_Δt – период наблюдения, год

;

n_o.c – число наблюдаемых отопительных сезонов, год;

h_o.c – продолжительность отопительного сезона, ч;

h_год – продолжительность года, ч;

i – порядковый номер объекта (района теплоснабжения); i = 1, 2,…, N;

j – порядковый номер диаметра трубопровода; j = 1, 2,…, R.

На основании исходной информации определяется параметр потока отказов трубопроводами тепловых сетей, характеризующий число отказов в течение года трубопроводом длиной в один километр.

Первоначально вычисляется параметр потока отказов трубопроводами по диаметрам d_j

(5.1)

По найденным значениям вычисляют математическое ожидание параметра потока отказов трубопроводов тепловых сетей

(5.2)

Для определения параметра потока отказов сосредоточенных элементов (задвижек, насосных блоков) линейные размеры l и d в матрице исходной информации отсутствуют.

По данным пассивного эксперимента [] повреждения, зафиксированные в трех районах г. Москва с 1994 по 1997 года, были проанализированы и исключены повреждения, не имеющей случайной природы и не приводящие к отказам. Все участки трубопроводов и их отказы были классифицированы по диаметрам от 200 до 1400 мм.

Так как повреждения фиксировались в течение отопительного периода, поэтому время наблюдения следует считать равным четырем отопительным сезонам. Для Москвы длительность отопительного периода равна 205 дням, или 0,562 года. Следовательно, при расчете параметра потока отказов время наблюдения равно года. Результаты пассивного эксперимента по трем тепловым районам и их результаты обработки представлены в табл. 5.1.

Значения параметра потока отказов определены для каждого диаметра трубопровода по формуле (5.1).

Среднее значение потока отказов является оценкой математического ожидания

(5.3)

R – число рассматриваемых диаметров труб;

– поток отказов трубопроводов с диаметром d_j;

Характеристики j = 1…R, R = 13	Диаметр трубопроводов, мм																				Всего
	200	250	300	350	400	450	500	600	700			800	1000			1200	1400
Протяженность труб (подающих + обратных), км, lj	401,1	60,2	87,5	22,7	113,3	13	136,1	66,9	31			41,9	36,1			57,7	27		1094,5
Число отказов kj	9	11	14	1	7	5	17	1	4			1	0			0	1		71
Параметр отказов ωTj, (км·год)-1	0,01	0,081	0,071	0,02	0,027	0,171	0,056	0,034	0,057			0,011	–			–	0,016		0,554
Среднее время восстановления zв, ч	6,27	6,61	5,38	4	7,57	6,2	13,12	8	24,65			4	–			–	5		90,8

Статистические данные по отказам на теплопроводах

за период эксплуатации с 1994 по 1997 г

Примечание. Среднее значение параметра потока отказов для труб всех диаметров

.

Оценка математического ожидания является более достоверной по сравнению со средним значением ω_ср = 0,0288, полученным для всей протяженности труб, без учета особенности их работы от диаметра.

Оценка дисперсии составляет

Средняя квадратичная погрешность серии наблюдений равна

При числе степеней свободы и доверительной вероятности P₀(t), принимаемой для технических расчетов 0,95 вычислим квантиль распределения Стьюдента по приближенной формуле с погрешностью не более 0,2 %

β – коэффициент доверия.

Таким образом, доверительный интервал случайной величины равен

Следовательно, с доверительной вероятностью 0,95 величина потока отказов трубопроводов тепловых сетей ω_T не может быть менее 0,015 и более 0,067.

По данным статистических наблюдений пассивного эксперимента величина расчетного значения параметра потока отказов теплопроводов, с учетом прогресса техники, принята = 0,05 (км·год)^-1 и задвижек год^-1 несколько заниженной, чтобы побудить заинтересованность к техническому прогрессу по надежности элементов.

При реконструкции систем теплоснабжения для оставляемых тепловых сетей, рекомендуется принимать (км·год)^-1.

По результатам многолетних испытаний получено уравнение для расчета времени восстановления теплопроводов, ч

(5.4)

где d – диаметр трубопровода, м.

Установлено, что время ремонта включает по продолжительности: слив воды 8%, собственно время ремонта 78% и время наполнения трубопроводов 14%.

Время ремонта трубопроводов зависит от типа прокладки трубопроводов (надземная или подземная) и расстояния между секционирующими задвижками, влияющими на время опорожнения и заполнения секции водой.

Поэтому точнее отражает продолжительность восстановительных работ трубопроводов тепловых сетей следующая формула, ч

(5.4a)

где – длина секции между секционирующими задвижками, км;

α – булева переменная; принимает значение 1 для подземной прокладки трубопроводов и 0 – надземной.

Показатель надежности функционирования системы

тепловых сетей

В основу принципа расчленения системы тепловых сетей на два иерархических уровня положено условие управляемости системой, т.е. поддержание её в работоспособном состоянии при обеспечении качественного теплоснабжения. Качество теплоснабжения выражается через величину математического ожидания отключаемой при авариях тепловой мощности РТП, а работоспособность – через вероятность безотказной работы при наработке на отказ. Такая постановка позволит численно определить эффективную мощность РТП исходя из времени ремонтно-восстановительных работ и значений параметра потока отказов элементов системы теплоснабжения.

В качестве критерия количественной оценки надежности системы тепловых сетей принят вероятный показатель надежности функционирования системы тепловых сетей P_с.т(t), который характеризуется качеством функционирования и её работоспособностью при наработке на отказ, учитываемой комплексом .

Таким образом, вероятностный показатель надежности функционирования систем тепловых сетей выражается зависимостью

(5.11)

при ограничении

где – математическое ожидание относительной остаточной мощности системы тепловых сетей в аварийной ситуации; вычисляется по формуле (5.14);

P_m(t) – вероятность m отказов системы за время t; вычисляется по формуле (5.16);

m – число отказов системы тепловых сетей за время t; вычисляется по формуле (5.17);

– коэффициент снижения цены отказа системы по отношению к системе мощностью 3000 МВт

;

z – продолжительность восстановления головного участка системы, ч

;

– продолжительность восстановления головного участка системы мощностью 3000 МВт, ч

.

На основании условия однозначности представляется возможным вероятностный показатель надежности функционирования системы тепловых сетей, выразить экспоненциальной зависимостью при .

(5.11a)

где – параметр потока нарушений качества теплоснабжений в результате аварийных ситуаций, год^-1; вычисляется по формуле (5.13б);

– параметр потока m отказов системы тепловых сетей за время t, год^-1; вычисляется по формуле (5.13а).

Математическое ожидание остаточной мощности системы тепловых сетей в аварийной ситуации вычисляется на основании системы уравнений Колмогорова.

, (5.12)

здесь правая часть уравнения выражает сумму вероятных мощностей системы находящихся в работоспособном и остаточной в отказовом состояниях

,

– вероятность работоспособности системы

;

P(t) – вероятность отказа системы

;

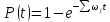– остаточная мощность системы в аварийной ситуации, МВт.

Запишем остаточную мощность системы в аварийной ситуации через отключаемую

;

где – расчетная мощность системы, МВт;

– отключаемая в аварийной ситуации мощность, МВт.

С учетом полученного выражения имеем формулу для вычисления математического ожидания отключаемой мощности зон (потребителей) в аварийной ситуации.

.

Используя условие однозначности для формулы (5.11) получим экспоненциальную зависимость вероятностного показателя надежности функционирования системы тепловых сетей

(5.11б)

где – параметр потока нарушений надежности теплоснабжения в результате аварийных отказов системы тепловых сетей, год^-1

(5.13)

– параметр потока m отказов системы тепловых сетей за время t, год^-1

; (5.13а)

– вероятность m отказов системы тепловых сетей за время t; вычисляется по формуле (5.16)

– параметр потока нарушений качества теплоснабжения в результате аварийных отказов системы тепловых сетей, год^-1

(5.13б)

– математическое ожидание относительной остаточной мощности системы тепловых сетей в аварийной ситуации

Формулу переправерить

(5.14)

где l – число отключаемых за год тепловых зон (пунктов) в аварийных ситуациях;

ω_j – параметр потока отказов отключаемой зоны, год^-1;

– мощность отключаемой зоны, МВт.

Параметр потока нарушений качества теплоснабжений ω_k зависит от величины отключаемой, в аварийной ситуации, мощности.

Вероятностный показатель надежности функционирования системы тепловых сетей дает оценку надежности её функционирования, определяя структуру и резерв системы.

Необходимо отметить, что показатель надежности построен в предположении вероятности возникновения отказов, а при возникновении отказа считается, что система попала в «поглощающее состояние» из которого выйти не может (система рассматривается как неремонтируемая). Таким образом, показатель надежности системы тепловых сетей учитывает вероятность возникновения отказов и их цену в виде отключаемой за год мощности потребителей.

При расчете математического ожидания отключаемой мощности РТП используется выражение:

или

Здесь второй сомножитель является средней величиной фактически отключаемой за год мощности

, (5.15)

при этом отражает общее количество отказов в системе за год, а – отключаемую за год мощность, зависящую от частоты отказов эквивалентированного элемента сети j.

Для потока отказов элементов тепловой сети приемлем закон массового обслуживания, из которого следует, что среднее число отказов за время t равно .

Вероятность m отказов за время t рассчитывается по закону Пуассона:

(5.16)

где m – вероятность m отказов за время t – величина целая .

. (5.17)

Использование формулы Стирлинга для приближенного вычисления факториала

Преобразует формулу Пуассона к виду

. (5.16а)

Вероятность безотказной работы системы тепловых сетей составляет

С достаточной для практических расчетов достоверностью можно принять

,

тогда формула Пуассона упрощается

. (5.16б)

Вероятность безотказной работы системы тепловых сетей составляет

,

а вероятность свершения хотя бы одного отказа вычисляется по формуле

Если вероятность отказовых состояний системы за время t приближается к единице, тогда математическое ожидание отключаемой мощности мало отличается от среднего значения фактически отключаемой мощности . Для больших по мощности систем тепловых сетей эти величины близки.

Связь между и выражается соотношением

. (5.15а)

Нормирование показателя надежности системы тепловых сетей

Нормированная величина показателя надежности системы тепловых сетей обеспечивает их проектирование и функционирование с заданными параметрами надежности.

Предлагается следующая методика нормирования показателя надежности системы тепловых сетей:

1) из анализа организации эксплуатационной службы теплопроводов и РТП, возможностей и времени изменения режимов работы ТП и теплообменников систем горячего водоснабжения, а также других эксплуатационных операций, связанных с проведением ремонтно-восстановительных работ, устанавливает нормированную величину средней фактически отключаемой мощности РТП при любых аварийных ситуациях на нерезервированной части тепловой сети в течение года. В качестве нормированной величины рекомендуется принимать МВт; сумму параметров потока отказов системы тепловых сетей можно принять пропорционально общей её тепловой мощности

, (5.18)

здесь – удельный нормативный параметр потока отказов тепловой сети ; рекомендуется принимать .

3) для принятых значений вычисляют нормированную величину математического ожидания относительной остаточной мощности в аварийной ситуации

, (5.19)

где – нормативная вероятность отказа системы тепловых сетей

,

m – число отказов за время t – есть величина целая .

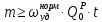; (5.20)

4) рассчитывает нормативную величину показателя надежности функционирования системы тепловых сетей

(5.21)

где – нормативная вероятность m отказов системы тепловых сетей за время t

(5.22)

5) нормированный коэффициент лимитированного теплоснабжения резервированных потребителей, на период аварийной ситуации, характеризует долю подачи теплоты от расчетной мощности теплопотребления из условия обеспечения лиметированным потребителям температуры воздуха помещений .

, (5.23)

а при заданном коэффициенте лимитированного теплоснабжения K_л определяется температура воздуха внутри помещений на период окончания ремонтно-восстановительных работ

, (5.24)

где – текущая и расчетная температуры воздуха помещений, °С;

– текущая температура наружного воздуха и расчетная для проектирования систем отопления, °С;

β – коэффициент аккумуляции зданий, ч; принимает β = 35…45 ч;

z – продолжительность восстановительных работ отказного участка сети, ч

d – диаметр трубопровода отказного участка сети, м;