§ 9.4 Распределение молекул газа по скоростям (распределение Максвелла)

При изучении газов принята основная модель — модель идеального газа как большого коллектива невзаимодействующих частиц, непрерывно участвующих в беспорядочном тепловом движении. К этому коллективу частиц применим статистический метод, базирующийся на математиче­ской теории вероятностей, на понятиях о средних, среднеквадратичных и наиболее вероятных параметрах, характеризующих поведение частиц в коллективе.

Рассмотрим распределение Максвелла или распределение молекул по скоростям.

Скорости молекул газа имеют различные значения и направления, причём как величина, так и направление скорости каждой отдельной молекулы изменяются в результате соударений, поэтому нельзя определить число молекул, обладающих точно заданной скорости в данный момент времени, но можно подсчитать число молекул, скорости которых лежат в интервале от υ₁ до υ₂.

Такая теоретическая зависимость была установлена Максвеллом на основании теории вероятностей: число молекул dN, скорость которых лежит в узком интервале между υ и υ +dυ, пропорциональна общему числу молекул N, ширине интервала dυ и зависит от скорости υ.

(9.36)

Функцию

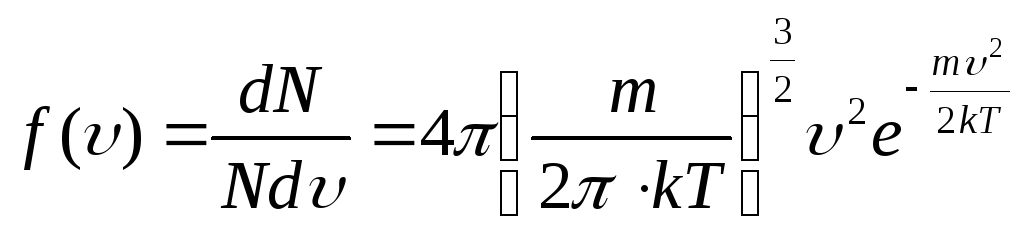(9.37)

показывающую относительное число молекул, скорость которых лежит в интервале скоростей dυ, называют функцией распределения молекул газа по скоростям.

Графически эта функция показана на рис. 9.12, а. За­штрихованная площадкаf(υ)dυ равна dN/N, т. е. относительному числу молекул газа, скорости которых лежат в интервале от υ до υ + dυ. Макси­мум кривой распределения соответствует наиболее вероятной скорости молекул υ_В, которую можно найти, исследовав на максимум функцию f(υ).

Беря производную от

(9.38)

по скорости и приравнивая её нулю, получаем

,

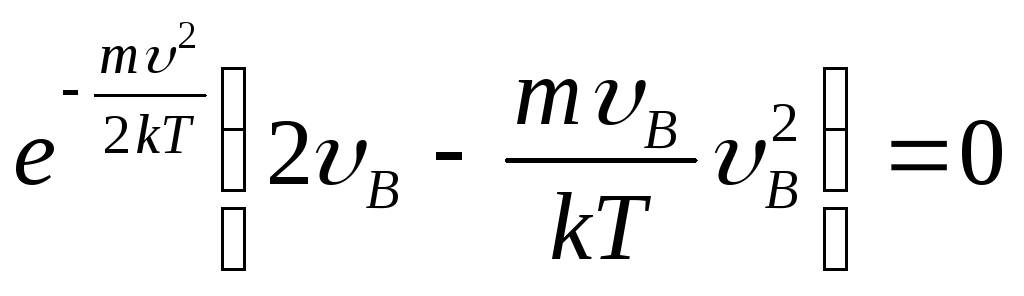
откуда

(9.39)

- наиболее вероятная скорость молекул газа.

Именно около этого (а не среднего, которое в 1.13 раза больше) значения группируется большинство скоростей, с которыми движутся молекулы газа.

Вид функции распределения f(υ) зависит от рода газа (массы моле­кул) и температуры Т. Давление и объем газа на распределение молекул по скоростям не влияют.

При повышении температуры (Т₂ > Т₁) υ_В возрастает, поэтому мак­симумы кривой распределения молекул по скоростям сдвигаются в сторону больших скоростей (υ₂>υ₁); следовательно, с ростом температуры возрастает относительное число молекул, обладающих большой скоростью. Площади, ограниченные кри­выми 1 и 2 (рис. 9.12, б), должны быть равны между собой, так как их величина пропорцио­нальна общему числу молекул, которое в обоих случаях сохра­няется неизменным.

Кроме наиболее вероятной скорости движение молекул газа характеризует средняя арифметическая скорость, определяемая формулой

(9.40)

- средняя арифметическая скорость молекул газа и

(9.41)

- средняя квадратическая скорость молекул газа Функция распределения молекул по энергии имеет вид

(9.42)

Средняя кинетическая энергия молекулы идеального газа определяется интегралом

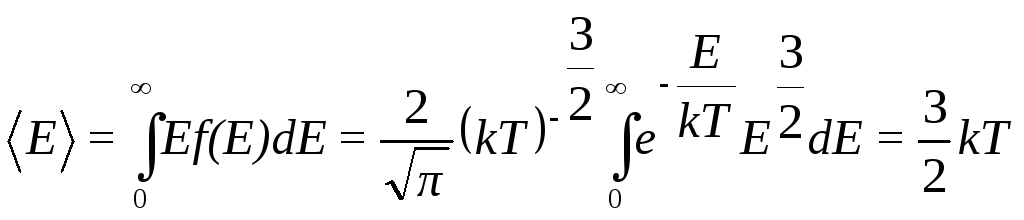(9.43)

Опыт Штерна. Одним из первых экспериментов, в котором были измерены скорости движения отдельных молекул газа, был опыт, выполненный немецким физиком Отто Штерном в 1920г. В опыте использовался прибор, состоящий из двух цилиндров разного радиуса с общей осью вращения рис. По оси цилиндра была расположена платиновая проволока, покрытая серебром. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропусканииэлектрического токачерез проволоку в результате её нагревания до температуры плавления серебра, происходило испарение атомов серебра с поверхности проволоки.Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее и оседать на внутренней стенке второго цилиндра, образуя на ней заметную полоску.

Затем всю систему начинали вращать с некой достаточно большой частотой ν. При этом полоса налёта смещалась в сторону, противоположную направлению вращения, и теряла чёткость. Измерив угол φ между этими двумя положениями полоски (рис.), расстоянию ℓ=R₁-R₂ и частоте вращения ν цилиндров можно было определить скорость атомов серебра.

(9.44)

Найденные из таких измерений значения скорости движения атомов серебра, оказались совпадающими со значениями, полученными на основе молекулярно-кинетической теории.

Размытость полоски свидетельствовала о том, что скорости атомов серебра, испаряющиеся с проволоки различны и распределены по закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее.

Опыт являлся одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.